福建省南平市2022届高三数学联考试卷
试卷更新日期:2021-10-18 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、2. 2021年8月8日,第32届夏季奥林匹克运动会在日本东京正式闭.17天的比赛全部结束后,排名前十的金牌数如下表所示,则这10个数据的中位数是( )
排名
1
2
3
4
5
6
7
8
9
10
国家/地区
美国
中国
日本
英国
俄罗斯奥运队
澳大利亚
荷兰
法国
德国
意大利
金牌数
39
38
27
22
20
17
10
10
10
10
A、18.5 B、18 C、19.5 D、203. 将函数 的图象向左平移 个单位长度,再将得到的图象上的所有点的横坐标变为原来的2倍(纵坐标不变),最后得到函数 的图象,则 ( )A、 B、 C、 D、4. 已知四边形 为梯形,则“ ”是“四边形 为等腰梯形”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 若直线 与曲线 相切,则( )A、 为定值 B、 为定值 C、 为定值 D、 为定值6. 已知单位向量 , 的夹角为 ,则 的最小值为( )A、 B、 C、 D、7. 已知定义在 上的偶函数 满足 ,当 时, 单调递增,则( )A、 B、 C、 D、8. 根据《民用建筑工程室内环境污染控制标准》,文化娱乐场所室内甲醛浓度 为安全范围.已知某新建文化娱乐场所施工中使用了甲醛喷剂,处于良好的通风环境下时,竣工1周后室内甲醛浓度为 ,3周后室内甲醛浓度为 ,且室内甲醛浓度 (单位: )与竣工后保持良好通风的时间 (单位:周)近似满足函数关系式 ,则该文化娱乐场所竣工后的甲醛浓度若要达到安全开放标准,至少需要放置的时间为( )A、5周 B、6周 C、7周 D、8周二、多选题
-
9. 若实数 , 满足 ,则( )A、 的共轭复数为 B、 C、 的值可能为 D、10. 下列函数中,最小值为9的是( )A、 B、 C、 D、11. 已知函数 ,则( )A、 的最大值为 B、 的图象关于点 对称 C、 图象的对称轴方程为 D、 在 上有4个零点12. 定义在 上的函数 的导函数为 ,且 恒成立,则必有( )A、 B、 C、 D、
三、填空题
-
13. 展开式中的第3项为.14. 设等差数列 的前 项和为 ,已知 ,则 .15. 已知 不是常数函数,写出一个同时具有下列四个性质的函数 :.
①定义域为R;② ;③ ;④ .
16. 设函数 关于 的方程 有四个实根 , , , ,则 的最小值为.四、解答题
-
17. 如图,在 中, 是 边上一点, , , .
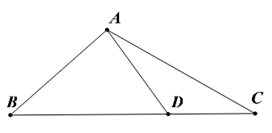 (1)、求角 的大小;(2)、若 ,求 和 .18. 如图,在四棱锥 中,底面 为矩形, 平面 , ,点 , 分别为 , 的中点.
(1)、求角 的大小;(2)、若 ,求 和 .18. 如图,在四棱锥 中,底面 为矩形, 平面 , ,点 , 分别为 , 的中点. (1)、证明: 平面 .(2)、若 ,求平面 与平面 所成锐二面角的余弦值.19. 已知数列 的前 项和为 ,且 ,数列 的前 项积为 ,且 .(1)、求 , 的通项公式;(2)、求数列 的前 项和 .20. 某地区位于甲、乙两条河流的交汇处,夏季多雨,根据统计资料预测,今年汛期甲河流发生洪水的概率为0.25,乙河流发生洪水的概率为0.2(假设两河流发生洪水与否互不影响),今年夏季该地区某工地有许多大型设备,为保护设备,有以下3种方案:方案一:不采取措施,当一条河流发生洪水时,设备将受损,损失30000元.当两河流同时发生洪水时,设备将受损,损失60000元.方案二:修建保护围墙,建设费为4000元,但围墙只能抵御一条河流发生的洪水,当两河流同时发生洪水时,设备将受损,损失60000元.方案三:修建保护大坝,建设费为9000元,能够抵御住两河流同时发生洪水.(1)、求今年甲、乙两河流至少有一条发生洪水的概率;(2)、从花费的角度考虑,试比较哪一种方案更好,说明理由.
(1)、证明: 平面 .(2)、若 ,求平面 与平面 所成锐二面角的余弦值.19. 已知数列 的前 项和为 ,且 ,数列 的前 项积为 ,且 .(1)、求 , 的通项公式;(2)、求数列 的前 项和 .20. 某地区位于甲、乙两条河流的交汇处,夏季多雨,根据统计资料预测,今年汛期甲河流发生洪水的概率为0.25,乙河流发生洪水的概率为0.2(假设两河流发生洪水与否互不影响),今年夏季该地区某工地有许多大型设备,为保护设备,有以下3种方案:方案一:不采取措施,当一条河流发生洪水时,设备将受损,损失30000元.当两河流同时发生洪水时,设备将受损,损失60000元.方案二:修建保护围墙,建设费为4000元,但围墙只能抵御一条河流发生的洪水,当两河流同时发生洪水时,设备将受损,损失60000元.方案三:修建保护大坝,建设费为9000元,能够抵御住两河流同时发生洪水.(1)、求今年甲、乙两河流至少有一条发生洪水的概率;(2)、从花费的角度考虑,试比较哪一种方案更好,说明理由.