北师版八年级数学上册《第四章 一次函数》单元检测A卷
试卷更新日期:2021-10-17 类型:单元试卷
一、单选题
-
1. 已知点 , 在一次函数 的图象上,则 与 的大小关系是( )A、 B、 C、 D、无法确定2. 如图,一次函数y=2x+1的图象与坐标轴分别交于A,B两点,O为坐标原点,则△AOB的面积为( )
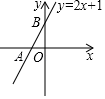 A、 B、 C、2 D、43. 已知一次函数 的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )A、 B、 C、 D、4. 快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程 与它们的行驶时间 之间的函数关系.小欣同学结合图像得出如下结论:
A、 B、 C、2 D、43. 已知一次函数 的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )A、 B、 C、 D、4. 快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程 与它们的行驶时间 之间的函数关系.小欣同学结合图像得出如下结论:①快车途中停留了 ;②快车速度比慢车速度多 ;③图中 ;④快车先到达目的地.其中正确的是( )
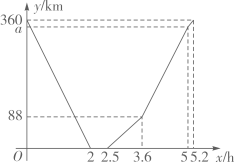 A、①③ B、②③ C、②④ D、①④5. 在平面直角坐标系中,若将一次函数 的图象向左平移3个单位后,得到个正比例函数的图象,则m的值为( )A、-5 B、5 C、-6 D、66. 小风在1000米中长跑训练时,已跑路程x(米)与所用时间t(秒)之间的函数图象如图所示,下列说法错误的是( )
A、①③ B、②③ C、②④ D、①④5. 在平面直角坐标系中,若将一次函数 的图象向左平移3个单位后,得到个正比例函数的图象,则m的值为( )A、-5 B、5 C、-6 D、66. 小风在1000米中长跑训练时,已跑路程x(米)与所用时间t(秒)之间的函数图象如图所示,下列说法错误的是( )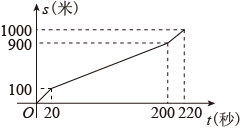 A、小风的成绩是220秒 B、小风最后冲刺阶段的速度是5米/秒 C、小风第一阶段与最后冲刺阶段速度相等 D、小风的平均速度是4米/秒7. 一次函数 的图象过点 , , ,则( )A、 B、 C、 D、8. 点 在函数 的图象上,则代数式 的值等于( )A、5 B、-5 C、7 D、-69. 一次函数 的图象如图所示,则下列结论正确的是( )
A、小风的成绩是220秒 B、小风最后冲刺阶段的速度是5米/秒 C、小风第一阶段与最后冲刺阶段速度相等 D、小风的平均速度是4米/秒7. 一次函数 的图象过点 , , ,则( )A、 B、 C、 D、8. 点 在函数 的图象上,则代数式 的值等于( )A、5 B、-5 C、7 D、-69. 一次函数 的图象如图所示,则下列结论正确的是( )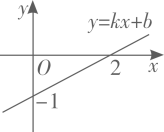 A、 B、 C、 随 的增大而减小 D、当 时,10. 数形结合是解决数学问题常用的思思方法.如图,直线y=x+5和直线y=ax+b,相交于点P ,根据图象可知,方程x+5=ax+b的解是( )
A、 B、 C、 随 的增大而减小 D、当 时,10. 数形结合是解决数学问题常用的思思方法.如图,直线y=x+5和直线y=ax+b,相交于点P ,根据图象可知,方程x+5=ax+b的解是( ) A、x=20 B、x=5 C、x=25 D、x=1511. 已知A,B两地相距60km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3h到达,乙骑摩托车.比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )
A、x=20 B、x=5 C、x=25 D、x=1511. 已知A,B两地相距60km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3h到达,乙骑摩托车.比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )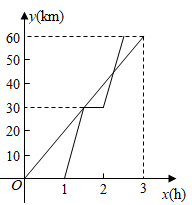 A、15km B、16km C、44km D、45km12. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返同,且往返速度的大小不变,两车离甲地的距离 (单位: )与慢车行驶时间 (单位: )的函数关系如图,则两车先后两次相遇的间隔时间是( )
A、15km B、16km C、44km D、45km12. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返同,且往返速度的大小不变,两车离甲地的距离 (单位: )与慢车行驶时间 (单位: )的函数关系如图,则两车先后两次相遇的间隔时间是( )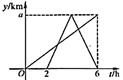 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 一次函数 的值随 值的增大而减少,则常数 的取值范围是.14. 将直线 向下平移2个单位长度,平移后直线的解析式为.15. 甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:
甲:函数的图象经过点(0,1);
乙:y随x的增大而减小;
丙:函数的图象不经过第三象限.
根据他们的叙述,写出满足上述性质的一个函数表达式为 .
16. 如图,一次函数 与坐标轴分别交于 , 两点,点 , 分别是线段 , 上的点,且 , ,则点 的标为.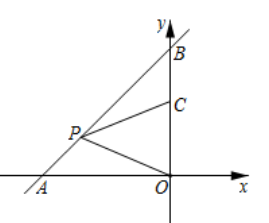 17. 下表中记录了一次试验中时间和温度的数据.
17. 下表中记录了一次试验中时间和温度的数据.时间/分钟
0
5
10
15
20
25
温度/℃
10
25
40
55
70
85
若温度的变化是均匀的,则14分钟时的温度是℃.
18. 如图,在平面直角坐标系中,直线y=﹣ x+4与x轴、y轴分别交于A、B两点,点C在第二象限,若BC=OC=OA,则点C的坐标为.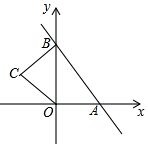
三、解答题
-
19. 在平面直角坐标系 中,一次函数 的图象由函数 的图象平移得到,且经过点(1,2).(1)、求这个一次函数的解析式;(2)、当 时,对于 的每一个值,函数 的值大于一次函数 的值,直接写出 的取值范围.20. I号无人机从海拔10m处出发,以10m/min的速度匀速上升,II号无人机从海拔30m处同时出发,以a(m/min)的速度匀速上升,经过5min两架无人机位于同一海拔高度b(m).无人机海拔高度y(m)与时间x(min)的关系如图.两架无人机都上升了15min.
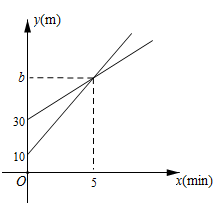 (1)、求b的值及II号无人机海拔高度y(m)与时间x(min)的关系式.(2)、问无人机上升了多少时间,I号无人机比II号无人机高28米.21. 在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成的长方形的周长与面积的数值相等,则这个点叫做和谐点,如图,过点P分别作x轴、y轴的垂线,若与坐标轴围成的长方形OAPB的周长与面积的数值相等,则点P是和谐点.
(1)、求b的值及II号无人机海拔高度y(m)与时间x(min)的关系式.(2)、问无人机上升了多少时间,I号无人机比II号无人机高28米.21. 在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成的长方形的周长与面积的数值相等,则这个点叫做和谐点,如图,过点P分别作x轴、y轴的垂线,若与坐标轴围成的长方形OAPB的周长与面积的数值相等,则点P是和谐点. (1)、请判断点M(1,3),N(3,6)是不是和谐点,并说明理由;(2)、若和谐点P(a,3)在直线y=x+3b(b为常数)上,求a、b的值.22. 甲超市在端午节这天进行苹果优惠促销活动,苹果的标价为10元 ,如果一次购买 以上的苹果,超过 的部分按标价6折售卖. (单位: )表示购买苹果的重量, (单位:元)表示付款金额.(1)、文文购买 苹果需付款元,购买 苹果需付款元;(2)、求付款金额 关于购买苹果的重量 的函数解析式;(3)、当天,隔壁的乙超市也在进行苹果优惠促销活动,同样的苹果的标价也为10元 ,且全部按标价的8折售卖.文文如果要购买 苹果,请问她在哪个超市购买更划算?23. A,B两家超市平时以同样的价格出售相同的商品.暑假期间两家超市都进行促销活动,促销方式如下:
(1)、请判断点M(1,3),N(3,6)是不是和谐点,并说明理由;(2)、若和谐点P(a,3)在直线y=x+3b(b为常数)上,求a、b的值.22. 甲超市在端午节这天进行苹果优惠促销活动,苹果的标价为10元 ,如果一次购买 以上的苹果,超过 的部分按标价6折售卖. (单位: )表示购买苹果的重量, (单位:元)表示付款金额.(1)、文文购买 苹果需付款元,购买 苹果需付款元;(2)、求付款金额 关于购买苹果的重量 的函数解析式;(3)、当天,隔壁的乙超市也在进行苹果优惠促销活动,同样的苹果的标价也为10元 ,且全部按标价的8折售卖.文文如果要购买 苹果,请问她在哪个超市购买更划算?23. A,B两家超市平时以同样的价格出售相同的商品.暑假期间两家超市都进行促销活动,促销方式如下:A超市:一次购物不超过300元的打9折,超过300元后的价格部分打7折;
B超市:一次购物不超过100元的按原价,超过100元后的价格部分打8折.
例如,一次购物的商品原价为500元,
去A超市的购物金额为: (元);
去B超市的购物金额为: (元).
(1)、设商品原价为x元,购物金额为y元,分别就两家超市的促销方式写出y关于x的函数解析式;(2)、促销期间,若小刚一次购物的商品原价超过200元,他去哪家超市购物更省钱?请说明理由.24. 已知一次函数y=k(x﹣3)(k≠0).(1)、求证:点(3,0)在该函数图象上.(2)、若该函数图象向上平移2个单位后过点(4,﹣2),求k的值.(3)、若k<0,点A(x1 , y1),B(x2 , y2)在函数图象上,且y1<y2 , 判断x1﹣x2<0是否成立?请说明理由.25. 如图,直线 与 轴交于点 ,与 轴交于点 ,点 为射线 上的一点(点 不与点 重合), 是 的中线,点 , 关于 对称,设点 的横坐标为 . (1)、求点 , 的坐标,若 ,求 所在直线的解析式;(2)、若 ,求 的值;(3)、若点 在 轴下方,直接写出 的取值范围.
(1)、求点 , 的坐标,若 ,求 所在直线的解析式;(2)、若 ,求 的值;(3)、若点 在 轴下方,直接写出 的取值范围.