初中数学浙教版七年级上册期中专题复习：实数的运算

试卷更新日期：2021-10-15 类型：复习试卷

进入出卷网下载

一、单选题

1. 在实数 $- 1$ ， $- \sqrt{2}$ ，0， $\frac{1}{4}$ 中，最小的实数是（）．

A、 $- 1$ B、 $\frac{1}{4}$ C、0 D、 $- \sqrt{2}$

查看试题解析
2. 计算 $- {(\sqrt{2})}^{2} + {(\sqrt{2} + π)}^{0} + {(- \frac{1}{2})}^{- 2}$ 的结果是（）

A、1 B、2 C、 $\frac{11}{4}$ D、3

查看试题解析
3. 下列计算正确的是（）

A、 $- 2 + (- 6) = 8$ B、 ${(- 2)}^{3} = - 6$ C、 $(- 2) \div \frac{1}{4} \times (- 2) = 4$ D、 $\sqrt[3]{- 27} = - 3$

查看试题解析
4. 下列运算中，结果最大的是（）．

A、2+(-3) B、2×(-3) C、2-(-3) D、-3²

查看试题解析
5. $- \sqrt{2}$ 的倒数的平方是（）

A、2 B、 $\frac{1}{2}$ C、-2 D、- $\frac{1}{2}$

查看试题解析
6. 计算 $\sqrt{2} \times \sqrt{8} +^{3} \sqrt{- 27}$ 的结果为（）

A、-1 B、1 C、4-3 $\sqrt{3}$ D、7

查看试题解析
7. 若x为实数，在 $(\sqrt{3} + 1) □ x$ 的“ $□$ ”中添上一种运算符号（在＋，－，×，÷中选择）后，其运算的结果是有理数，则x不可能的是（）

A、 $\sqrt{3} + 1$ B、 $\sqrt{3} - 1$ C、 $2 \sqrt{3}$ D、 $1 - \sqrt{3}$

查看试题解析
8. 若 $\sqrt[3]{3}$ 取1.442，计算 $\sqrt[3]{3} - 3 \sqrt[3]{3} - 98 \sqrt[3]{3}$ 的结果是（）

A、-100 B、-144.2 C、144.2 D、-0.01442

查看试题解析
9. 化简1-|1- $\sqrt{2}$ |的结果是（）

A、 $- \sqrt{2}$ B、 $2 - \sqrt{2}$ C、 $\sqrt{2}$ D、 $2 + \sqrt{2}$

查看试题解析
10. 若a，b互为相反数，c，d互为倒数，m的绝对值为2，则m²-cd+ $\frac{a + b}{m}$ 值为（）

A、-3 B、3 C、-5 D、3或-5

查看试题解析

二、填空题

11. $\sqrt{1 - \frac{9}{25}} + \sqrt{0.04} +^{3} \sqrt{{(- 2)}^{3}} + | \sqrt{\frac{1}{4} - 1} |$ =

查看试题解析
12. 计算： $|^{3} \sqrt{8} - 4 | - {(\frac{1}{2})}^{- 2}$ =

查看试题解析
13. 计算： $\sqrt[3]{- 8} - | - \sqrt{16} | =$ .

查看试题解析
14. 计算：(π+1)⁰+| $\sqrt{3}$ -2|-( $\frac{1}{2}$ )^-2=

查看试题解析
15. 计算﹣1²⁰²¹+2021⁰﹣|﹣ $\sqrt{4}$ |＝．

查看试题解析
16. 计算 $\sqrt{81} + | 2 - \sqrt{3} | + \sqrt[3]{- 125} + 6 \div (- \frac{3}{4})$ = ．

查看试题解析

三、解答题

17. 计算： $| - 2 \sqrt{3} | + {(4 + π)}^{0} -^{3} \sqrt{27} + {(- 1)}^{2020}$

查看试题解析
18. 计算：( $\frac{1}{2}$ )^－¹－|－1＋ $\sqrt{2}$ |＋2cos45°＋(－1－ $\sqrt{3}$ )⁰.

查看试题解析
19. 学习第 $3$ 章《实数》时，甲、乙两名同学提出两个结论：
甲：存在两个不相等的非整数的有理数，它们商是整数；
乙：存在两个不相等的无理数，它们的和是整数；
请你判断两人的说法是正确还是错误．如果正确，举出一个例子；如果错误，说明理由．

查看试题解析
20. 化简求值：|1﹣ |+| |+| |．

查看试题解析
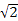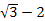21. 一堆玩具分给若干个小朋友，若每人分3件，则剩余4件；若前面每人分4件，则最后一人能得到的玩具不足3件，求小朋友的人数及玩具数．

查看试题解析
22. 设 $S_{1} = 1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}$ ， $S_{2} = 1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}$ ， $S_{3} = 1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}$ ，…， $S_{n} = 1 + \frac{1}{n^{2}} + \frac{1}{{(n + 1)}^{2}}$ ．若 $S = \sqrt{S_{1}} + \sqrt{S_{2}} + \dots + \sqrt{S_{n}}$ ，求S（用含n的代数式表示，其中n为正整数）．

查看试题解析
23. 求1+2+2²+2³+…+2²⁰¹⁵的值，可令S=1+2+2²+2³+…+2²⁰¹⁵ ，则2S=2+2²+2³+2⁴+…+2²⁰¹⁶ ，因此2S﹣S=2²⁰¹⁶﹣1．仿照以上推理，计算出1+5+5²+5³+…+5²⁰¹⁵的值．

查看试题解析
24. 化简求值：（ $\frac{a}{a + 2} + \frac{1}{a^{2} - 4}$ ） $\div \frac{a - 1}{a + 2} + \frac{1}{a - 2}$ ，其中a=2+ $\sqrt{2}$ ．

查看试题解析
25. （1）计算：| $\sqrt{2}$ ﹣ $\sqrt{7}$ |+2 $\sqrt{2}$ ；
（2）求式子中的x：（1﹣x）³=64．

查看试题解析
26. 阅读下面的文字，解答问题：大家知道 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分我们不可能全部地写出来，于是小明用 $\sqrt{2}$ -1来表示 $\sqrt{2}$ 的小数部分，你同意小明的表示方法吗？
事实上，小明的表示方法是有道理，因为 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分。

又例如：

∵ $\sqrt{4}$ < $\sqrt{7}$ < $\sqrt{9}$ ，即2< $\sqrt{7}$ <3，

∴ $\sqrt{7}$ 的整数部分为2，小数部分为( $\sqrt{7}$ -2)．

请解答：

(1)、 $\sqrt{17}$ 的整数部分是，小数部分是。

(2)、如果 $\sqrt{5}$ 的小数部分为a， $\sqrt{13}$ 的整数部分为b，求a+b- $\sqrt{5}$ 的值；

(3)、已知：10+ $\sqrt{3}$ =x+y，其中x是整数，且0<y<1，求x-y的相反数。

查看试题解析