河南省漯河市2020-2021学年高一上学期数学期末考试试卷
试卷更新日期:2021-10-15 类型:期末考试
一、单选题
-
1. 若集合 , ,那么 ( )A、 B、 C、 D、2. 直线 ,若 ,则 的倾斜角是( )A、30° B、60° C、120° D、150°3. 已知 、 是两条不同的直线, 是一个平面,则下列结论正确的是( )A、若 , ,则 B、若 , ,则 C、若 , ,则 D、若 , ,则4. 设 ,则 的大小关系是( )A、 B、 C、 D、5. 我国著名数学家华罗庚先生曾说:“数缺形时少直观,形缺数时难入微,数形结合百般好,隔离分家万事休.”在数学学习和研究中,我们要学会以形助数.则在同一直角坐标系中, 与 的图像可能是( )A、
 B、
B、 C、
C、 D、
D、 6. 两直线3x+4y-2=0与6x+8y-5=0的距离等于 ( )A、3 B、7 C、 D、7. 下列函数为奇函数的是( )A、 B、 C、 D、8. 圆心在 轴上,且过点 的圆与 轴相切,则该圆的方程是A、 B、 C、 D、9. 长方体 中, ,异面直线 和 所成角的正切值是( )A、 B、 C、 D、10. 已知函数 ,若 ,则 的取值范围是( )A、 B、 C、 D、11. 直线 与曲线 交于M、N两点,O为坐标原点,当 面积取最大值时,实数k的值为A、 B、 C、-1 D、112. 如图所示正三棱锥 中, 是 上一点, ,且 , ,则三棱锥 的外接球的表面积为( )
6. 两直线3x+4y-2=0与6x+8y-5=0的距离等于 ( )A、3 B、7 C、 D、7. 下列函数为奇函数的是( )A、 B、 C、 D、8. 圆心在 轴上,且过点 的圆与 轴相切,则该圆的方程是A、 B、 C、 D、9. 长方体 中, ,异面直线 和 所成角的正切值是( )A、 B、 C、 D、10. 已知函数 ,若 ,则 的取值范围是( )A、 B、 C、 D、11. 直线 与曲线 交于M、N两点,O为坐标原点,当 面积取最大值时,实数k的值为A、 B、 C、-1 D、112. 如图所示正三棱锥 中, 是 上一点, ,且 , ,则三棱锥 的外接球的表面积为( ) A、2π B、 C、4π D、6π
A、2π B、 C、4π D、6π二、填空题
-
13. 已知圆 关于直线 对称,则 .14. 已知函数 ,对于任意的 , ,当 时, ,则 .15. 已知底面半径和高都为 的圆锥,其内接圆柱的高为 ,则这个圆柱的侧面积为 .16. 已知圆 ,过圆外一点 作圆的两条切线 (切点为 ),则直线 的方程为 .
三、解答题
-
17. 已知函数 ,对于任意的 , .(1)、若 ,求 的解析式;(2)、若 在 上有零点,求实数 的取值范围.18. 如图所示长方体 中, , 是 的中点.
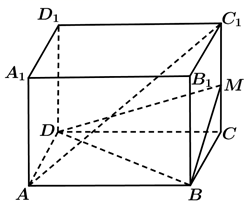 (1)、证明: 平面 ;(2)、若 是 的中点,求三棱锥 的体积.19. 已知全集 ,集合 , .(1)、当 时,求 ;(2)、如果 ,求实数 的取值范围.
(1)、证明: 平面 ;(2)、若 是 的中点,求三棱锥 的体积.19. 已知全集 ,集合 , .(1)、当 时,求 ;(2)、如果 ,求实数 的取值范围.
