河北省张家口市2020-2021学年高一上学期数学期末考试试卷

试卷更新日期：2021-10-15 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x \in N | - 1 < x \leq 4}$ ， $B = {- 1 ， 1 ， 3 ， 5}$ ，则 $A \cup B =$ （）

A、 ${0 ， 4}$ B、 ${1 ， 3}$ C、 ${- 1 ， 1 ， 2 ， 3 ， 4 ， 5}$ D、 ${- 1 ， 0 ， 1 ， 2 ， 3 ， 4 ， 5}$

查看试题解析
2. 命题“ $\forall α > β$ ， $\sin α > \sin β$ ”的否定为（）

A、 $\forall α > β$ ， $\sin α \leq \sin β$ B、 $\forall α ⩽ β$ ， $\sin α > \sin β$ C、 $\exists α > β$ ， $\sin α \leq \sin β$ D、 $\exists α ⩽ β$ ， $\sin α \leq \sin β$

查看试题解析
3. 某学校大门口有一座钟楼，每到夜晚灯光亮起都是一道靓丽的风景，有一天因停电导致钟表慢10分钟，则将钟表拨快到准确时间分针所转过的弧度数是（）

A、 $- \frac{π}{3}$ B、 $- \frac{π}{6}$ C、 $\frac{π}{6}$ D、 $\frac{π}{3}$

查看试题解析
4. 若 $a \in R$ ，则“ $a^{3} > 1$ ”是“ $a^{2} > 1$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
5. 函数 $f (x) = x^{2} - \frac{1}{| x |}$ 的图象大致为（）

A、 B、 C、 D、

查看试题解析
6. 设 $a = {0.5}^{- 1.2}$ ， $b = {0.4}^{0.5}$ ， $c = \log_{0.4} 1.2$ ，则a，b，c的大小关系是（）

A、 $a < b < c$ B、 $c < a < b$ C、 $c < b < a$ D、 $b < a < c$

查看试题解析
7. 已知 $x > 0$ ， $y > 0$ ，且 $x + 4 y = 1$ ，则 $\frac{x + y}{x y}$ 的最小值为（）

A、4 B、9 C、10 D、12

查看试题解析
8. 已知关于 $x$ 的方程 $\lg^{2} x + a \lg x + b = 0$ 的两个实数根分别是 $x_{1}$ 、 $x_{2}$ ，若 $x_{1} \cdot x_{2} = 100$ ，则 $b$ 的取值范围为（）

A、 $[2 ， 100]$ B、 $[0 ， 2]$ C、 $[1 ， 100]$ D、 $(- \infty ， 1]$

查看试题解析

二、多选题

9. 定义集合A的真子集的非空真子集为集合A的孙集，设集合 $A = {0 ，$ 1，2， $3}$ ，则A的孙集可以是（）

A、{0} B、 ${1 ，$ 2， $3}$ C、 ${1 ， 2}$ D、 ${0 ， 3}$

查看试题解析
10. 设函数 $f (x) = {\begin{array}{l} 1 - x ， x \leq a \\ 2^{x} ， x > a \end{array}$ ，若 $f (1) = 2 f (0)$ ，则实数 $a$ 可以为（）

A、-1 B、0 C、1 D、2

查看试题解析
11. 已知角α的顶点与原点重合，始边与x轴的非负半轴重合，终边经过点 $P (m ， 1 - m)$ ，若 $m > 0$ ，则下列各式一定为正值的是（）

A、 $\sin α$ B、 $\cos α$ C、 $\sin α - \cos α$ D、 $\sin α + \cos α$

查看试题解析
12. 已知函数 $f (x) = | 2^{x} - 1 |$ ，实数 $a$ 、 $b$ 满足 $f (a) = f (b) (a < b)$ ，则下列结论正确的有（）

A、 $2^{a} + 2^{b} > 2$ B、 $\exists a$ 、 $b$ ，使 $0 < a + b < 1$ C、 $2^{a} + 2^{b} = 2$ D、 $a + b < 0$

查看试题解析

三、填空题

13. 函数 $f (x) = a^{x + 2} ， (a > 0 ， a \neq 1)$ 的图像恒过定点

查看试题解析
14. 已知幂函数 $f (x) = m x^{n} + k$ 的图象过点 $(\frac{1}{16} ， \frac{1}{4})$ ，则 $m - 2 n + 3 k =$ .

查看试题解析
15. 把物体放在冷空气中冷却，如果物体原来的温度是θ₁℃，空气的温度是θ₀℃，那么tmin后物体的温度θ（单位： ℃ ）可由公式 $θ = θ_{0} + (θ_{1} - θ_{0}) e^{- kt}$ （k为正常数）求得.若 $k = \frac{1}{2} \ln 2$ ，将55 ℃ 的物体放在15 ℃ 的空气中冷却，则物体冷却到35 ℃ 所需要的时间为 min .

查看试题解析
16. 已知函数 $f (x) = \log_{2} (a x^{2} - a x + 4)$ .

(1)、若 $f (x)$ 在 $[\frac{1}{2} ， 2)$ 上单调递减，则实数 $a$ 的取值范围是；

(2)、若 $f (x)$ 的值域是 $R$ ，则实数 $a$ 的取值范围是.

查看试题解析

四、解答题

17. 已知集合 $A = {x | 2 - b < a x \leq 2 b - 2}$ ， $B = {x | - \frac{1}{2} < x \leq 2}$ $(a \neq 0)$ ．

(1)、若 $a = 1$ ， $b = 3$ ，求 $A \cap (∁_{R} B)$ ；

(2)、集合A，B能否相等？若能，求出a，b的值；若不能，请说明理由．

查看试题解析
18. 已知 $\frac{2 \cos α + \sin α}{\sin α - \cos α} = 4$ .

(1)、求 $\tan α$ 的值；

(2)、若 $π < α < 2 π$ ，求 $\frac{\cos (4 π - α) \cdot \sin (α - \frac{π}{2}) \cdot \cos (α + \frac{3 π}{2})}{\sin (\frac{π}{2} + α) \cdot \sin (- α)}$ 的值.

查看试题解析
19. 为持续推进“改善农村人居环境，建设宜居美丽乡村”，某村委计划在该村广场旁一矩形空地进行绿化.如图所示，两块完全相同的长方形种植绿草坪，草坪周围（斜线部分）均摆满宽度相同的花，已知两块绿草坪的面积均为400平方米.

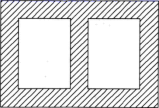(1)、若矩形草坪的长比宽至少多9米，求草坪宽的最大值；

(2)、若草坪四周及中间的花坛宽度均为2米，求整个绿化面积的最小值.

查看试题解析
20. 已知函数 $f (x) = x^{2} - 2 (a + 1) x + 4 a$ .

(1)、若 $a = \frac{1}{2}$ ，解不等式 $f (x) > 0$ ；

(2)、解关于x的不等式 $f (x) < 0$ .

查看试题解析
21. 已知函数 $f (x)$ 是定义在 $R$ 上的奇函数，且 $x \in (- \infty ， 0)$ 时， $f (x) = - {(x - 1)}^{2}$ .

(1)、求函数 $f (x)$ 的解析式；

(2)、若 $f (a \cdot 2^{- x}) + f (- 2 - 2^{x}) < 0$ 任意 $x$ 恒成立，求实数 $a$ 的取值范围.

查看试题解析
22. 已知函数 $f (x) = \ln x - m$ .

(1)、若函数 $g (x) = f (x) + e x$ 在区间 $(\frac{1}{e} ， 1)$ 内存在零点，求实数m的取值范围；

(2)、若关于x的方程 $f (e^{x} + 1) = \frac{x}{2}$ 有实数根，求实数m的取值范围.

查看试题解析