初中数学浙教版九年级上册专题复习：二次函数的图象与性质

试卷更新日期：2021-10-15 类型：复习试卷

进入出卷网下载

一、单选题

1. 抛物线y=x²-4x+3的对称轴是直线（）

A、x=-2 B、x=2 C、x=-4 D、x=4

查看试题解析
2. 在平面直角坐标系中，将抛物线y=2x²-4先向右平移2个单位长度，再向上平移1个单位长度得到的拋物线对应的函数表达式是（）

A、y=2(x+2)²+3 B、y=2(x+2)²-3 C、y=2(x-2)²+3 D、y=2(x-2)²-3

查看试题解析
3. 由抛物线y=x²平移得到抛物线y=(x+2)² ，下列平移方法可行的是（）

A、向上平移2个单位长度 B、向下平移2个单位长度 C、向左平移2个单位长度 D、向右平移2个单位长度

查看试题解析
4. 二次函数y=ax²+bx+c的图像如图所示，根据图像可得a，b，c与0的大小关系是（）

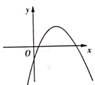A、a>0，b<0，c<0 B、a>0，b>0，c>0 C、a<0，b<Q，c<0 D、a<0，b>0，c<0

查看试题解析
5. 二次函数y=(x-1)²+3的顶点坐标是（）

A、(1，3) B、(1，-3) C、(-1，3) D、(-1，-3)

查看试题解析
6. 下列函数中，属于二次函数的是（　　）

A、y=x﹣3 B、y=x²﹣（x+1）² C、y=x（x﹣1）﹣1 D、 $y = \frac{1}{x^{2}}$

查看试题解析
7. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0) \neq$ 的图象如图所示，给出以下结论：① $b^{2} > 4 a c$ ；② $a b c > 0$ ；③ $2 a - b = 0$ ；④ $8 a + c < 0$ ；⑤ $9 a + 3 b + c < 0$ .其中结论正确的个数有（）

A、1 B、2 C、3 D、4

查看试题解析
8. 二次函数 $y = k x^{2} + 2 x + 1 (k < 0)$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
9. 已知A、B两点的坐标分别为（3，﹣4）、（0，﹣2），线段AB上有一动点M（m，n），过点M作x轴的平行线交抛物线y＝a（x﹣1）²+2于P（x₁ ， y₁）、Q（x₂ ， y₂）两点.若x₁＜m≤x₂ ，则a的取值范围为（）

A、﹣4≤a＜﹣ $\frac{3}{2}$ B、﹣4≤a≤﹣ $\frac{3}{2}$ C、﹣ $\frac{3}{2}$ ≤a＜0 D、﹣ $\frac{3}{2}$ ＜a＜0

查看试题解析
10. 已知二次函数 $y = (a - 1) x^{2}$ ，当 $x > 0$ 时，y随x增大而增大，则实数a的取值范围是（）

A、 $a > 0$ B、 $a > 1$ C、 $a \neq 1$ D、 $a < 1$

查看试题解析

二、填空题

11. 二次函数y= $- \frac{1}{2}$ (x-3)²的图像的开口方向是(填“向上”或“向下")．

查看试题解析
12. 若抛物线y=ax²+(a+3)x-2(a≠0)开口向上，且当x>-1时，y随x值的增大而增大，则满足条件的a的取值范围是

查看试题解析
13. 若函数y=(m-2)x^|m|+1(m是常数)是二次函数，则m的值是

查看试题解析
14. 抛物线y=(x+2)(x-1)的对称轴是直线

查看试题解析
15. 如图，直线AB与抛物线y=ax²+bx+c(a>0)相交于A(-2，5)，B(5，12)两点，点P是抛物线上位于直线AB下方的点，则点P的横坐标m的取值范围是

查看试题解析
16. 抛物线 $y = 2 {(x - 2)}^{2} - 4$ 的顶点坐标是.

查看试题解析

17. 抛物线

y = a x^{2} + b x + c

上部分点的横坐标x，纵坐标y的对应值如表：则抛物线的对称轴是.

x	…	-2	-1	0	1	2	…
y	…	0	4	6	6	4	…

查看试题解析

三、解答题

18. 若二次函数y=ax²+bx+c的图象的顶点是（2，1）且经过点（1，2），求此二次函数解析式．

查看试题解析
19. 写出抛物线 $y = x^{2} - 4 x - 3$ 的开口方向、对称轴和顶点坐标.

查看试题解析
20. 已知抛物线 $y = x^{2} + 2 x + m - 3$ 的顶点在第二象限，求 $m$ 的取值范围．

查看试题解析
21. 已知二次函数y＝﹣2x²﹣4x+1，先用配方法转化成y＝a（x﹣h）²+k，再写出函数的顶点坐标、对称轴以及描述该函数的增减性.

查看试题解析
22. 有三位同学分别说出了二次函数的图象与性质：
甲：抛物线的开口向上；

乙：抛物线与x轴没有交点；

丙：当x>-2时，y随x的增大而增大。

请写出一个符合上述条件的二次函数表达式。

查看试题解析
23. 画出函数的图象，写出它的开口方向，对称轴和顶点，并说明当y随x的增大而增大时，x的取值范围．

查看试题解析
24. 已知函数y=m• $x^{m^{2} + m}$ ，m²+m是不大于2的正整数，m取何值时，它的图象开口向上？当x取何值时，y随x的增大而增大？当x取何值时，y随x的增大而减少？当x取何值时，函数有最小值？

查看试题解析

四、综合题

25. 已知，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象与x轴相交于点A，B（点A在点B的左侧），与y轴相交于点C.

(1)、若 $a = - 1$ ，如图1，已知A，C两点的坐标为 $A (- 1 ， 0) ， C (0 ， 3)$ .
①求抛物线的解析式，并求出B的坐标.

②点P是抛物线上第一象限内一个动点.y轴上有一点 $D (0 ， 1)$ ，连结 $D P$ 交 $B C$ 于点H，若H恰好平分 $D P$ ，求点P的坐标.

(2)、若 $a = 1$ ， $b = k - 1$ ， $c = - k$ ， $k > 0$ ，如图2，抛物线与一次函数 $y = k x + 1$ 的图象交于E，F两点，点E在点F的左侧.在直线 $E F$ 上是否存在唯一一点Q，使得 $∠ A Q O = 90 °$ ？若存在，请求出此时k的值；若不存在，请说明理由.

查看试题解析
26. 已知抛物线 $y = x^{2} + (k^{2} + k - 6) x + 3 k$ （ $k$ 为常数）的对称轴是y轴，并且与x轴有两个交点.

(1)、求k的值；

(2)、若点P在抛物线 $y = x^{2} + (k^{2} + k - 6) x + 3 k$ 上，且点P到y轴的距离是2，求点P的坐标.

查看试题解析
27. 如图，在平面直角坐标系中，已知 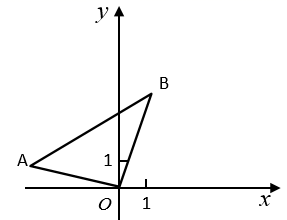$△ A O B$ ， $∠ A O B = 90 °$ ， $A O = B O$ ，点 $A$ 的坐标为 $(- 3 ， 1)$ .

(1)、求点 $B$ 的坐标.

(2)、求过点 $A$ ， $O$ ， $B$ 的二次函数的表达式.

(3)、设点 $B$ 关于二次函数的对称轴 $l$ 的对称点为 $B_{1}$ ，求 $△ A B_{1} B$ 的面积.

查看试题解析
28. 如图，在平面直角坐标系中，二次函数 $y = a x^{2} + b x + 4 (a \neq 0)$ 的图象经过 $A (- 3 ， 0)$ ， $B (4 ， 0)$ 两点，且与 $y$ 轴交于点 $C$ .点 $D$ 为 $x$ 轴负半轴上一点，且 $B C = B D$ ，点 $P$ ， $Q$ 分别在线段 $A B$ 和 $C A$ 上.

(1)、求这个二次函数的表达式.

(2)、若线段 $P Q$ 被 $C D$ 垂直平分，求 $A P$ 的长.

(3)、在第一象限的这个二次函数的图象上取一点 $G$ ，使得 $S_{△ G C B} = S_{△ G C A}$ ，再在这个二次函数的图象上取一点 $E$ （不与点 $A$ ， $B$ ， $C$ 重合），使得 $∠ G B E = 45 °$ ，求点 $E$ 的坐标.

查看试题解析
29. 在平面直角坐标系中，二次函数图象的表达式为y＝ax²＋(a＋1)x，其中a≠0.

(1)、若此函数图象过点(1，－3)，求这个二次函数的表达式；

(2)、若(x₁ ， y₁)，(x₂ ， y₂)为此函数图象上的两个不同点，
①若x₁＋x₂＝2，则y₁＝y₂ ，试求a的值；

②当x₁＞x₂≥－2，对任意的x₁ ， x₂都有y₁＞y₂ ，试求a的取值范围.

查看试题解析