湖北省黄石市2020-2021学年七年级上学期数学12月月考试卷

试卷更新日期：2021-10-15 类型：月考试卷

进入出卷网下载

一、单选题

1. 温度由﹣4℃上升7℃是（）

A、3℃ B、﹣3℃ C、11℃ D、﹣11℃

查看试题解析
2. 一个正常人的心跳平均每分钟70次，一天大约跳的次数用科学记数法表示这个结果是（）.

A、1.008×10⁵ B、100.8×10³ C、5.04×10⁴ D、504×10³

查看试题解析
3. 实数a在数轴上对应的点如图所示，则a、－a、1的大小关系正确的是（）

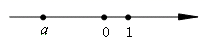A、－a＜a＜1 B、a＜－a＜1 C、1＜－a＜a D、a＜1＜－a

查看试题解析
4. 下列去括号正确的是（）

A、 $- 3 a - (2 b - c) = - 3 a + 2 b - c$ B、 $- 3 a - (2 b - c) = - 3 a - 2 b - c$ C、 $- 3 a - (2 b - c) = - 3 a + 2 b + c$ D、 $- 3 a - (2 b - c) = - 3 a - 2 b + c$

查看试题解析
5. 若 $- 3 x y^{2 m}$ 与 $5 x^{2 n - 3} y^{8}$ 的和是单项式，则m、n的值分别是（）

A、m=2，n=2 B、m=4，n=2 C、m=4，n=1 D、m=2，n=3

查看试题解析
6. 若方程4x﹣1=3x+1和2m+x=1的解相同，则m的值为（）

A、﹣3 B、1 C、- $\frac{1}{2}$ D、 $\frac{3}{2}$

查看试题解析
7. 轮船在静水中速度为每小时20km，水流速度为每小时4km，从甲码头顺流行驶到乙码头，再返回甲码头，共用5小时（不计停留时间），求甲、乙两码头的距离，设两码头间的距离为xkm，则列出方程正确的是（）.

A、（20＋4）x＋（20－4）x＝5 B、20x＋4x＝5 C、 $\frac{x}{20} + \frac{x}{4} = 5$ D、 $\frac{x}{20 + 4} + \frac{x}{20-4} = 5$

查看试题解析
8. 关于x，y的单项式 $a x^{2} y ， b x y^{2} ， \frac{1}{2} x^{2} y ， 3 x y^{2}$ 的和，合并同类项后结果是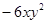，则 $a ， b$ 的值分别是（）

A、 $a = - \frac{1}{2} ， b = - 3$ B、 $a = - \frac{1}{2} ， b = - 9$ C、 $a = \frac{1}{2} ， b = - 9$ D、 $a = \frac{1}{2} ， b = 3$

查看试题解析
9. 我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题：”一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁?”意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完，试问大、小和尚各多少人?设大和尚有x人，依题意列方程得（）

A、 $\frac{x}{3} + 3 (100 - x)$ =100 B、 $3 x + \frac{100 - x}{3}$ =100 C、 $\frac{x}{3} - 3 (100 - x) = 100$ D、 $3 x - \frac{100 - x}{3} = 100$

查看试题解析
10. 计算机利用的是二进制数，它共有两个数码0、1，将一个十进制数转化为二进制，只需把该数写出若干2ⁿ数的和，依次写出1或0即可.如： $19_{(10)} = 16 + 2 + 1 = 1 \times 2^{4} + 0 \times 2^{3} + 0 \times 2^{2} + 1 \times 2^{1} + 1 = 10011_{(2)}$ 为二进制下的五位数.则十进制数1027是二进制下的（）.

A、九位数 B、十位数 C、十一位数 D、十二位数

查看试题解析

二、填空题

11. 数轴上表示数－5和表示－14的两点之间的距离是．

查看试题解析
12. 如果 $| x - 2 | + | y + 4 | = 0$ ，那么代数式y－x的值是.

查看试题解析
13. 写出单项式-3a²b的一个同类项：.

查看试题解析
14. 若多项式 $x^{2} - 3 k x y - 3 y^{2} + 6 x y - 8$ 不含 $x y$ 项，则 $k =$ .

查看试题解析
15. 长度相等而粗细不同的两支蜡烛，其中一支可燃3小时，另一支可燃4小时.将这两支蜡烛同时点燃，当余下的长度中，一支是另一支的3倍，蜡烛点燃了小时.

查看试题解析
16. 规定：符号“&”为选择两数中较大数的运算，“Δ”为选择两数中较小数的运算.则[（7Δ3）&6] $\times$ [5Δ（3&7）]的结果为.

查看试题解析

三、解答题

17. 计算：

(1)、12＋（－17）－（－23）

(2)、 $\frac{1}{2} \times (- \frac{2}{3}) \times (- 2 \frac{1}{4}) \times (- 5 \frac{1}{3})$

查看试题解析
18. 解方程：

(1)、3（x＋2）－2＝x＋2

(2)、 $\frac{7-5y}{6} = 1- \frac{3y-1}{4}$

查看试题解析
19. 在抗洪抢险中，解放军战士的冲锋舟加满油，沿东西方向的河流抢救灾民，早晨从A地出发，晚上到达B地，约定向东记为正，向西记为负，当天的航行路线记录如下（单位：千米）：
$14 ， - 9 ， + 8 ， - 7 ， + 13 ， - 6 ， + 12 ， - 5$ .

(1)、请你帮忙确定B地相对于A地的位置；

(2)、若冲锋舟每千米耗油0.5升，油箱容量为28升，冲锋舟在当天救灾过程中至少还需补充多少升油？

查看试题解析
20. 已知 $2 a - b = - 2$ ，求代数式 $3 (2 a b^{2} - 4 a + b) - 2 (3 a b^{2} - 2 a) + b$ 的值.

查看试题解析
21. 已知： $A = a x^{2} + x - 1$ ， $B = 3 x^{2} - 2 x + 1$ （ $a$ 为常数）

(1)、若 $A$ 与 $B$ 的和中不含 $x^{2}$ 项，求 $a$ 的值；

(2)、在（1）的条件下化简： $B - 2 A$ .

查看试题解析
22. 有理数 $a < 0$ ， $b > 0$ ， $c > 0$ ，且 $| c | < | b |$ .

(1)、在数轴上将 $b$ ， $c$ 两个数填在相应的横线上；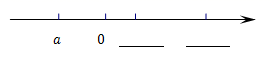

(2)、用“>”、“=”、“<”填空： $a - b$ 0， $b - c$ 0， $a - c$ 0；

(3)、化简： $| a - b | + 2 | b - c | - | a - c |$ .

查看试题解析
23. 某工厂车间有21名工人，每人每天可以生产12个螺钉或18个螺母，1个螺钉需要配2个螺母，为使每天生产的螺钉和螺母刚好配套，车间应该分配生产螺钉和螺母的工人各多少名.

查看试题解析
24. “水是生命之源”，某城市自来水公司为了鼓励居民节约用水，规定按以下标准收取水费：
用水量/月
单价（元/m³）
不超过20m³
2.8
超过20m³的部分
3.8
另：每立方米用水加收0.2元的城市污水处理费

(1)、如果1月份某用户用水量为19m³ ，那么该用户1月份应该缴纳水费元．

(2)、某用户2月份共缴纳水费80元，那么该用户2月份用水多少m³？

(3)、若该用户水表3月份出了故障，只有70%的用水量记入水表中，这样该用户在3月份只缴纳了58.8元水费，问该用户3月份实际应该缴纳水费多少元？

查看试题解析
25. 如图，在数轴上A点表示数a，B点示数b，C点表示数c，b是最小的正整数，且a、c满足|a+2|+（c﹣7）²=0.

(1)、a= ， b= ， c=；

(2)、若将数轴折叠，使得A点与C点重合，则点B与数表示的点重合；

(3)、点A、B、C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动，假设t秒钟过后，若点A与点B之间的距离表示为AB，点A与点C之间的距离表示为AC，点B与点C之间的距离表示为BC.则AB= ， AC= ， BC=.（用含t的代数式表示）

(4)、请问：3BC﹣2AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值.

查看试题解析

用水量/月	单价（元/m³）
不超过20m³	2.8
超过20m³的部分	3.8