初中数学浙教版八年级上册专题复习：勾股定理
试卷更新日期：2021-10-15 类型：同步测试
一、单选题
-
1. 一个直角三角形的两条直角边分别是5和12，则斜边长为（ ）A、15 B、13 C、12 D、102. 如图所示，在长方体ABCD-A1B1C1D1中，AB=3，BC=2，BB1=1，一只蚂蚁从A点出发，沿长方体表面爬到C1点处觅食，则蚂蚁所行路程的最小值的平方为（ ）
A、14 B、18 C、20 D、263. 下列长度的三条线段能组成直角三角形的是（ ）A、a=0.3，b=0.4，c=0.5 B、a= ，b= ，c= C、a=2m2+23，b= m2+15， c=m2+8 D、a=8，b=12，c=154. 如图，以直角三角形的三边为边向外作了三个正方形．已知正方形A面积为225，正方形B面积为289，则正方形C的边长为（ ）
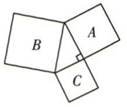A、64 B、514 C、8 D、115. 古埃及人曾经用如图所示的方法画直角：把一根长绳打上等距离的13个结，然后以3个结间距、4个结间距、5个结间距的长度为边长，用木桩钉成一个三角形，其中一角便是直角，这样做的道理是（ ）
A、直角三角形两个锐角互余 B、三角形内角和等于180° C、三角形任意两边之和大于第三边，任意两边之差小于第三边． D、如果三角形两边长的平方和等于第三边长的平方，那么这个三角形是直角三角形6. 三角形的三边长a，b，c，满足(c+b)2=a2+2bc，则这个三角形是（ ）A、锐角三角形 B、直角三角形 C、钝角三角形 D、等边三角形7. 下列各组数中，是勾股数的为（ ）A、0.3，0.4，0.5 B、8，15，17 C、5，6，7 D、2，0，58. 在下列说法中是错误的（ ）A、在△ABC中，∠C＝∠A一∠B，则△ABC为直角三角形． B、在△ABC中，若∠A：∠B：∠C＝5：2：3，则△ABC为直角三角形． C、在△ABC中，若 ， ， 则△ABC为直角三角形． D、在△ABC中，若a：b：c＝2：2：4，则△ABC为直角三角形．9. 我国古代数学著作《九章算术》中记载了一个问题：“今有池方一丈，葭（jiǎ）生其中，出水一尺，引葭赴岸，适与岸齐.间水深几何.”（丈、尺是长度单位，1丈 尺，）其大意为：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺.如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面，水的深度是多少？则水深为（ ）
A、10尺 B、11尺 C、12尺 D、13尺10. “赵爽弦图”是由4个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图所示）．若直角三角形的两条直角边的长分别是2和1，则图中阴影区域的面积与大正方形的面积之比为（ ）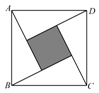
A、 B、 C、 D、二、填空题
-
11. 如图所示，小明和组员想知道在水平地面上立的旗杆是否垂直于地面，已知旗杆高20米．从旗杆顶部拉下来一根绳子，测得绳子一端离旗杆底部BC长15.5 米，绳子长25米．那么旗杆是否与地面垂直？答案为：(填“是”或“不是”)
12. 公元3世纪初，中国古代数学家赵爽注《周髀算经》时，创造了“赵爽弦图”如图所示，设勾a=6，弦c= 10，则小正方形ABCD的面积是
13. 如图，两个滑块M，N由一个连杆连接，分别可以在两条互相垂直的滑道上滑动．开始时，滑块M距O点20cm，滑块N距O点15cm，则当滑块M向下滑到O点时，滑块N滑动了
14. 一个游泳爱好者要横跨一条宽AC=8 m的河流，由于水流速度的原因，这位游泳爱好者向下游偏离了BC=6 m，这位游泳爱好者在横跨河流的实际游泳距离为米．
15. 如图所示，圆柱底面半径为 cm，高为9 cm，点A，B分别是圆柱两底面圆周上的点，且A，B在同一母线上，用一个棉线从A点顺着圆柱侧面绕3圈到B点，则这根棉线的长度最短为cm．
16. 如图所示，长方体的长为15，宽为10，高为20，点B离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是
17. 如图所示，等腰三角形ABC的底边为8cm，腰长为5cm ，一动点P（与B、C不重合）在底边上从B向C以1cm/s的速度移动，当P运动秒时，△ACP是直角三角形
18. 一个直角三角形面积为3，斜边长 ，则这个直角三角形的周长为 ．三、解答题
-
19. 为了缓解司机的视力疲劳，某隧道施工单位准备在双向道路中间全程增加一个宽为1米的长长的绿草坪．已知隧道截面是一个半径为4米的半圆形，点O是其圆心，AE是绿草坪的截面．问一辆高3米，宽1.9米的卡车能通过这个隧道吗？请说明理由．
20. 如图，在边长为1的正方形组成的网格中，有AB，CD，EF，GH四条线段，端点都在格点上，你能选取其中三条线段组成一个直角三角形吗？请说明理由．
21. 房屋建筑设计师掌握很多数学知识．一天，李师傅加工完一块板材有事离开了，走时，他给徒弟一个任务：测量一下这块三角形板材的∠N是不是直角．经过测量，发现MN=75米，NK=4米，MK=8.5米．请你帮徒弟想一想，怎么样才能说明∠N是直角？
22. 为了推广城市绿色出行，某市准备在AB路段建设一个共享单车停放点，该路段附近有两个广场C和D，如图所示，CA⊥AB于点A，DB⊥AB于点B，AB=1 700 m，CA=1 200m，DB=500m，试问这个单车停放点E应建在距点A多远处，才能使它到两广场的距离相等？
23. 在△ABC中，AB=15，AC=13，BC边上的高AD=12，求△ABC的周长．24. 在△ABC中，a，b，c是∠A，∠B，∠C的对边，a= ，b= ，c=2，△ABC是否为直角三角形？如果是直角三角形，请指出哪个角是直角．25. 如图，一辆卡车装满货物后，高4米，宽3米．这辆卡车能通过横截面如图所示(上面是一个半圆，下面是长方形)的隧道吗？
26. 某同学在喝易拉罐饮料的时候，发现如果沿着罐内壁BC竖直放置的吸管，露在外面的部分BD =2厘米；如果尽最大长度往里放置，吸管正好和罐顶持平．已知易拉罐的底部是直径AC长为8厘米的圆．请你求出吸管的长度和易拉罐的高度．
27. 在△ABC中，∠C=90° ，设AB=a，BC=c，AC=b．(1)、若c=8，b=15，求a的长；(2)、若a=13，b=5，求c的长．28. 在△ABC中，AB=c，BC=a，AC=b。如图①所示，当∠C=90°时，根据勾股定理，有a2+b2=c2。
(1)、如图②所示，当△ABC为锐角三角形时，类比勾股定理，判断a2+b2与c2的大小关系，并说明理由。(2)、如图③所示，当△ABC为钝角三角形时，类比勾股定理，判断a2+b2与c2的大小关系，并说明理由。29. 如图，在△ABC中，AB＝4，AC＝3，BC＝5，DE是BC的垂直平分线，交BC于点D ， AB于点E ．
(1)、求证：△ABC为直角三角形．(2)、求DE的长．30. 如图，Rt△ABC中，∠C= 90°，BC=4 cm，∠ABC=30°。点P从点B出发，沿B→A→C以每秒3cm的速度向终点C运动，同时点Q从点B出发以每秒、3cm的速度向终点C运动，其中一点到达终点即停止．设点P的运动时间为t。
(1)、当t=2秒时，求△BPQ的面积；(2)、PQ能否与△ABC的一条边平行，如果能，求出此时t的值；如不能，说明理由；(3)、△BPQ的面积能否为△ABC面积的三分之一？如果能，请求出的值；如果不能，请说明理由。