初中数学浙教版八年级上册专题复习:等腰三角形的性质与判定
试卷更新日期:2021-10-14 类型:复习试卷
一、单选题
-
1. 如图所示,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )
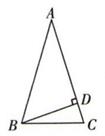 A、36° B、54° C、18° D、64°2. 等腰三角形的两边长分别为6和14,则这个等腰三角形的底边长是( )A、6 B、6或14 C、14 D、343. 若等腰三角形的顶角是40°,则它的底角是( )A、40° B、70° C、80° D、100°4. 已知a、b、c是 的三条边,且满足 ,则 是( )A、锐角三角形 B、钝角三角形 C、等腰三角形 D、等边三角形5. 如图,△ABC为等边三角形,∠ABC、∠ACB的平分线相交于点O,OE∥AB交BC于点E,OF∥AC交BC于点F,则图中等腰三角形共有( )
A、36° B、54° C、18° D、64°2. 等腰三角形的两边长分别为6和14,则这个等腰三角形的底边长是( )A、6 B、6或14 C、14 D、343. 若等腰三角形的顶角是40°,则它的底角是( )A、40° B、70° C、80° D、100°4. 已知a、b、c是 的三条边,且满足 ,则 是( )A、锐角三角形 B、钝角三角形 C、等腰三角形 D、等边三角形5. 如图,△ABC为等边三角形,∠ABC、∠ACB的平分线相交于点O,OE∥AB交BC于点E,OF∥AC交BC于点F,则图中等腰三角形共有( )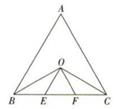 A、6个 B、5个 C、4个 D、3个6. AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于( )A、10 B、5 C、4 D、37. 如图, 中, , 平分 ,以下结论:
A、6个 B、5个 C、4个 D、3个6. AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于( )A、10 B、5 C、4 D、37. 如图, 中, , 平分 ,以下结论:①线段 是线段 的垂直平分线② 是等腰三角形;③ ;④ 为 的中点.其中正确的有( )
 A、1个 B、2个 C、3个 D、4个8. 如图,在△ABC中,AB=AC,在AB、AC上分别截取AP、AQ。使AP'=AQ。再分别以点P、Q为圆心,以大于 PQ的长为半径作弧,两弧在∠BAC内交于点R,作射线AR,交BC于点D。若BC=6,则BD的长为( )
A、1个 B、2个 C、3个 D、4个8. 如图,在△ABC中,AB=AC,在AB、AC上分别截取AP、AQ。使AP'=AQ。再分别以点P、Q为圆心,以大于 PQ的长为半径作弧,两弧在∠BAC内交于点R,作射线AR,交BC于点D。若BC=6,则BD的长为( )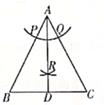 A、2 B、3 C、4 D、59. 直线 与坐标轴交于 、 两点,点 在坐标轴上, 为等腰三角形,则满足条件的点 最多有( )个A、8; B、4; C、5; D、7.10. 如图,AC , BD相交于点O , ∠A=∠D . 若请你再补充一个条件,使得△BOC是等腰三角形,则你补充的条件不能是( )
A、2 B、3 C、4 D、59. 直线 与坐标轴交于 、 两点,点 在坐标轴上, 为等腰三角形,则满足条件的点 最多有( )个A、8; B、4; C、5; D、7.10. 如图,AC , BD相交于点O , ∠A=∠D . 若请你再补充一个条件,使得△BOC是等腰三角形,则你补充的条件不能是( )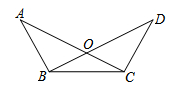 A、OA=OD B、AB=CD C、∠ABO=∠DCO D、∠ABC=∠DCB
A、OA=OD B、AB=CD C、∠ABO=∠DCO D、∠ABC=∠DCB二、填空题
-
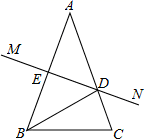
11. 如图已知∠B=∠C,请同学从这①BE=CE,②AB=DC,③∠BAE=∠CDE三个等式中再选出一个作为条件,可以推出△AED是等腰三角形的有(填序号).
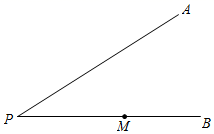
 12. 如图,∠AOB=60°,OC平分∠AOB,P为射线OC上一点,如果射线OA上的点D满足△OPD是等腰三角形,那么∠ODP的度数为
12. 如图,∠AOB=60°,OC平分∠AOB,P为射线OC上一点,如果射线OA上的点D满足△OPD是等腰三角形,那么∠ODP的度数为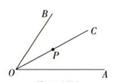 13. 等腰三角形ABC中,AB=AC,一腰上的中线把这个三角形的周长分成12和15两部分,则这个三角形的底边长为14. 等腰三角形的两边长分别为3和 ,则这个等腰三角形的周长是 .15. 过等腰三角形顶角顶点的一条直线,将该等腰三角形分成的两个三角形均为等腰三角形,则原等腰三角形的底角度数为 .16. 若一条长为 的细线能围成一边长等于 的等腰三角形,则该等腰三角形的腰长为cm.17. 在平面直角坐标系xOy中,A(0,2),B(0,6),动点C在直线y=﹣x上,若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数为 .18. 在等腰△ABC 中,AD⊥BC 交直线 BC 于点 D.若 AD=0.5BC,则△ABC 的顶角的度数为
13. 等腰三角形ABC中,AB=AC,一腰上的中线把这个三角形的周长分成12和15两部分,则这个三角形的底边长为14. 等腰三角形的两边长分别为3和 ,则这个等腰三角形的周长是 .15. 过等腰三角形顶角顶点的一条直线,将该等腰三角形分成的两个三角形均为等腰三角形,则原等腰三角形的底角度数为 .16. 若一条长为 的细线能围成一边长等于 的等腰三角形,则该等腰三角形的腰长为cm.17. 在平面直角坐标系xOy中,A(0,2),B(0,6),动点C在直线y=﹣x上,若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数为 .18. 在等腰△ABC 中,AD⊥BC 交直线 BC 于点 D.若 AD=0.5BC,则△ABC 的顶角的度数为三、解答题
-
19. 如图,在△ABC中,AB=AC,点D是BC的中点,点E在AB上,BE=BD,∠BAC=76°,求∠ADE的大小.
 20. 如图所示,已知点 , 在 的边 上, , .求证: .
20. 如图所示,已知点 , 在 的边 上, , .求证: .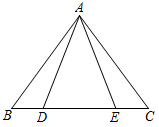 21. 已知:如图,AB=AC,∠ABD=∠ACD.求证:DB=DC.
21. 已知:如图,AB=AC,∠ABD=∠ACD.求证:DB=DC.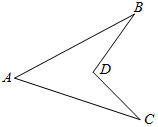 22. 如图,在 中, 和 的平分线交于点 ,过点 作 交 于点 ,交 于点 .若 , ,求线段 的长.
22. 如图,在 中, 和 的平分线交于点 ,过点 作 交 于点 ,交 于点 .若 , ,求线段 的长.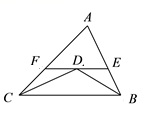 23. 如图所示, 的外角平分线 ,求证: 为等腰三角形.
23. 如图所示, 的外角平分线 ,求证: 为等腰三角形.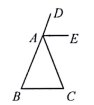 24. 如图,△ABC是等腰三角形,∠B=∠C,AD是底边BC上的高,DE∥AB交AC于点E.试说明△ADE是等腰三角形.
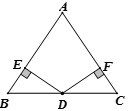
24. 如图,△ABC是等腰三角形,∠B=∠C,AD是底边BC上的高,DE∥AB交AC于点E.试说明△ADE是等腰三角形.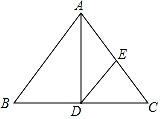 25. 已知:如图,D是△ABC的BC边的中点, , 且DE=DF.
25. 已知:如图,D是△ABC的BC边的中点, , 且DE=DF.求证:△ABC是等腰三角形.
四、综合题
-
26. 已知:如图,点D、E在 的边BC上, , .求证:
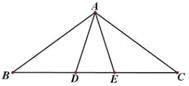 (1)、 ;(2)、若 , ,直接写出图中除 与 外所有的等腰三角形.27. 在四边形 中,已知 , , , .
(1)、 ;(2)、若 , ,直接写出图中除 与 外所有的等腰三角形.27. 在四边形 中,已知 , , , .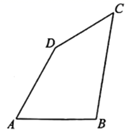 (1)、连接 ,试判断 的形状,并说明理由;(2)、求 的度数
(1)、连接 ,试判断 的形状,并说明理由;(2)、求 的度数