初中数学浙教版八年级上册专题复习:全等三角形的性质与判定
试卷更新日期:2021-10-14 类型:复习试卷
一、单选题
-
1. 如图, =90°,下列条件中,不能判定 与 全等的是( )
 A、 , B、 , C、 , D、 ,2. 如图,点B、E、C、F在同一直线上,∠ACB=∠F,添加下列条件仍不能判定△ABC与△DEF全等的是( )
A、 , B、 , C、 , D、 ,2. 如图,点B、E、C、F在同一直线上,∠ACB=∠F,添加下列条件仍不能判定△ABC与△DEF全等的是( ) A、∠A=∠D,AB=DE B、AC=DF,CF=BE C、AB=DE,AB∥DE D、∠A=∠D,∠B=∠DEF3. 已知如图,要测量水池的宽 ,可过点 作直线 ,再由点 观测,在 延长线上找一点 ,使 ,这时只要出 的长,就知道 的长,那么判定 △ 的理由是
A、∠A=∠D,AB=DE B、AC=DF,CF=BE C、AB=DE,AB∥DE D、∠A=∠D,∠B=∠DEF3. 已知如图,要测量水池的宽 ,可过点 作直线 ,再由点 观测,在 延长线上找一点 ,使 ,这时只要出 的长,就知道 的长,那么判定 △ 的理由是 A、 B、 C、 D、4. 如图, , 且 , ,下列结论:① ;② ;③ ;其中正确的结论是
A、 B、 C、 D、4. 如图, , 且 , ,下列结论:① ;② ;③ ;其中正确的结论是 A、①② B、①②③ C、①③ D、②③5. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在 的两边 、 上分别在取 ,移动角尺,使角尺两边相同的刻度分别与点 、 重合,这时过角尺顶点 的射线 就是 的平分线.这里构造全等三角形的依据是( )
A、①② B、①②③ C、①③ D、②③5. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在 的两边 、 上分别在取 ,移动角尺,使角尺两边相同的刻度分别与点 、 重合,这时过角尺顶点 的射线 就是 的平分线.这里构造全等三角形的依据是( )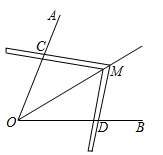 A、 B、 C、 D、6. 用直尺和圆规作一个角等于已知角,如图,能得出∠A'O'B'=∠AOB的依据是( )
A、 B、 C、 D、6. 用直尺和圆规作一个角等于已知角,如图,能得出∠A'O'B'=∠AOB的依据是( )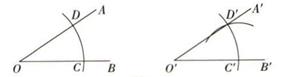 A、SAS B、SSS C、ASA D、AAS7. 如图是作△ABC的作图痕迹,则此作图的已知条件是( )
A、SAS B、SSS C、ASA D、AAS7. 如图是作△ABC的作图痕迹,则此作图的已知条件是( )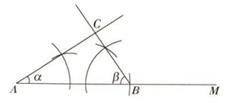 A、已知两边及夹角 B、已知三边 C、已知两角及夹边 D、已知两边及一边对角8. 根据下列已知条件,能作出唯一△ABC的是( )A、AB=3,BC=4,CA=8 B、AB=4,BC=3,∠A=60° C、∠A=60°,∠B=45°,AB=4 D、∠C=90°,∠B=30°,∠A=60°9. 如图,点 是 的中点, , 平分 ,下列结论∶① ② ③ ④ ,四个结论中成立的是( )
A、已知两边及夹角 B、已知三边 C、已知两角及夹边 D、已知两边及一边对角8. 根据下列已知条件,能作出唯一△ABC的是( )A、AB=3,BC=4,CA=8 B、AB=4,BC=3,∠A=60° C、∠A=60°,∠B=45°,AB=4 D、∠C=90°,∠B=30°,∠A=60°9. 如图,点 是 的中点, , 平分 ,下列结论∶① ② ③ ④ ,四个结论中成立的是( ) A、①②④ B、①②③ C、②③④ D、①③10. 如图,已知点B、C、E在一直线上, 、 都是等边三角形,联结 和 , 与 相交于点F , 与 相交于点G , 下列说法不一定正确的是( )
A、①②④ B、①②③ C、②③④ D、①③10. 如图,已知点B、C、E在一直线上, 、 都是等边三角形,联结 和 , 与 相交于点F , 与 相交于点G , 下列说法不一定正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若 , , ,则 的长为 .12. 如图,点B在AE上,∠CAB=∠DAB,要使△ABC≌△ABD,可补充的一个条件是:.(答案不唯一,写一个即可)
 13. 如图,△ABC≌△DBE,△ABC的周长为30,AB=9,BE=8,则AC的长是.
13. 如图,△ABC≌△DBE,△ABC的周长为30,AB=9,BE=8,则AC的长是.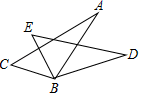 14. 如图,小明与小红玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50cm,当小红从水平位置CD下降30cm时,小明离地面的高度是cm.
14. 如图,小明与小红玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50cm,当小红从水平位置CD下降30cm时,小明离地面的高度是cm.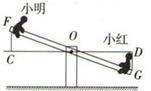 15. 有一座小山,现要在小山的A,B两端开一条隧道,如图,施工队要知道A,B之间的距离,于是先在平地上取一可以直接到达点A和点B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE.经测量,DE,EC,DC的长度分别为800m,500m,400m,则A,B之间的距离为m.
15. 有一座小山,现要在小山的A,B两端开一条隧道,如图,施工队要知道A,B之间的距离,于是先在平地上取一可以直接到达点A和点B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE.经测量,DE,EC,DC的长度分别为800m,500m,400m,则A,B之间的距离为m.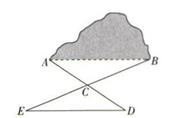 16. 如图,在四边形ABCD中,AD=AB,DC=BC,∠DAB=60°,∠DCB=120°,E在AD上,F是AB延长线上一点,且DE=BF,若G在AB上,且∠ECG=60°,则DE、EG、BG之间的数量关系是 .
16. 如图,在四边形ABCD中,AD=AB,DC=BC,∠DAB=60°,∠DCB=120°,E在AD上,F是AB延长线上一点,且DE=BF,若G在AB上,且∠ECG=60°,则DE、EG、BG之间的数量关系是 .
三、解答题
-
17. 如图,已知OA=OC,OB=OD,∠AOC=∠BOD.求证:△AOB≌△COD.
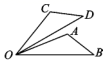 18. 如图,在 中,D是边 上的点, ,垂足分别为E,F,且 .求证: .
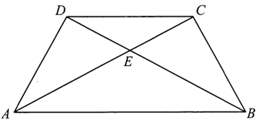
18. 如图,在 中,D是边 上的点, ,垂足分别为E,F,且 .求证: . 19. 已知:AB∥CD,BE、CF分别是∠ABC、∠BCD的平分线,O是BC的中点,则线段BE与线段CF有怎样的关系?请说明理由.
19. 已知:AB∥CD,BE、CF分别是∠ABC、∠BCD的平分线,O是BC的中点,则线段BE与线段CF有怎样的关系?请说明理由. 20. 如图,在□ABCD中,连接BD , 在BD的延长线上取一点E , 在DB的延长线上取一点F , 使BF=DE , 连接AF、CE . 求证:AF∥CE .
20. 如图,在□ABCD中,连接BD , 在BD的延长线上取一点E , 在DB的延长线上取一点F , 使BF=DE , 连接AF、CE . 求证:AF∥CE . 21. 如图,在 中, , ,点 是边 上一点, ,作 , 交边 于点 .求证: .
21. 如图,在 中, , ,点 是边 上一点, ,作 , 交边 于点 .求证: . 22. 如图,在 中,点 是边 的中点,过点 作直线 使 ,交 的延长线于点 .试说明 的理由.
22. 如图,在 中,点 是边 的中点,过点 作直线 使 ,交 的延长线于点 .试说明 的理由.
解:因为 (已知),
所以 ▲ ( )
因为点 是边 的中点,
所以 ▲
在 和 中,
所以 ( ▲ )
所以 ( ▲ )
23. 如图, , 是 上一点,且 平分 , 平分 ,求证: .