初中数学浙教版七年级上册6.6 角的大小比较 同步练习
试卷更新日期:2021-10-14 类型:同步测试
一、单选题
-
1. 下列图形中,能确定 的是( )A、
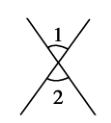 B、
B、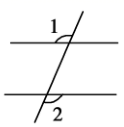 C、
C、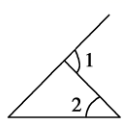 D、
D、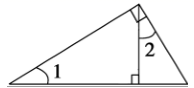 2. 如图,一副三角尺按不同的位置摆放,摆放位置中∠α与∠β一定相等的图形个数共有( )
2. 如图,一副三角尺按不同的位置摆放,摆放位置中∠α与∠β一定相等的图形个数共有( ) A、1个 B、2个 C、3个 D、4个3. 如图,在一副三角板中,标识了4个角,其中最大的角为( )
A、1个 B、2个 C、3个 D、4个3. 如图,在一副三角板中,标识了4个角,其中最大的角为( )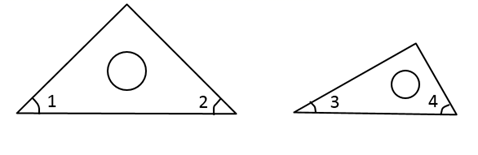 A、∠1 B、∠2 C、∠3 D、∠44. 如图,∠AOB=∠COD=90°,若∠BOD=150°,则∠BOC的度数为( )
A、∠1 B、∠2 C、∠3 D、∠44. 如图,∠AOB=∠COD=90°,若∠BOD=150°,则∠BOC的度数为( ) A、150° B、120° C、90° D、60°5. 借助一副三角板,你不能画出下面哪个度数的角( )A、 B、 C、 D、6. 如图, 与 相交于点 ,则下列结论正确的是( )
A、150° B、120° C、90° D、60°5. 借助一副三角板,你不能画出下面哪个度数的角( )A、 B、 C、 D、6. 如图, 与 相交于点 ,则下列结论正确的是( )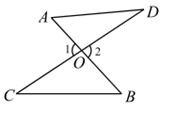 A、 B、 C、 D、7. 如图是黑板上出示的尺规作图题,需要回答横线上符号代表的内容( )
A、 B、 C、 D、7. 如图是黑板上出示的尺规作图题,需要回答横线上符号代表的内容( )如图,已知∠AOB , 求作:∠DEF , 使∠DEF=∠AOB .
作法:(1)以
 为圆心,任意长为半径,分别交OA , OB于点P , Q;
为圆心,任意长为半径,分别交OA , OB于点P , Q;(2)作射线EG , 并以点E为圆心,
 长为半径画弧,交EG于点D;
长为半径画弧,交EG于点D;(3)以点D为圆心,
 长为半径画弧,交第(2)步中所画弧于点F;
长为半径画弧,交第(2)步中所画弧于点F;(4)作
 ,∠DEF即为所作的角.
,∠DEF即为所作的角.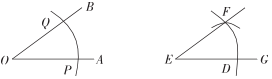 A、
A、 表示点E
B、
表示点E
B、 表示PQ
C、⊗表示OQ
D、⊕表示射线EF
8. 若 , , ,则下列结论正确的是( )A、 B、 C、 D、9. 如图,在△ 中, , 为钝角.按下列步骤作图:①以点B为圆心,适当长为半径作圆弧,交BC于点D,交AB于点E;②以点 为圆心, 长为半径作圆弧,交 于点 ;③以点 为圆心, 长为半径作圆弧,交②中所作的圆弧于点 ;④作射线 交 于点 .下列说法错误的是( )
表示PQ
C、⊗表示OQ
D、⊕表示射线EF
8. 若 , , ,则下列结论正确的是( )A、 B、 C、 D、9. 如图,在△ 中, , 为钝角.按下列步骤作图:①以点B为圆心,适当长为半径作圆弧,交BC于点D,交AB于点E;②以点 为圆心, 长为半径作圆弧,交 于点 ;③以点 为圆心, 长为半径作圆弧,交②中所作的圆弧于点 ;④作射线 交 于点 .下列说法错误的是( ) A、 = B、 =∠ACB C、∠CHB=∠A+∠B D、 =∠HCB10. 如图,CD为∠AOB的角平分线,射线OE经过点O且∠AOE=90°,若∠DOE=63°,则∠BOC的度数是( )
A、 = B、 =∠ACB C、∠CHB=∠A+∠B D、 =∠HCB10. 如图,CD为∠AOB的角平分线,射线OE经过点O且∠AOE=90°,若∠DOE=63°,则∠BOC的度数是( )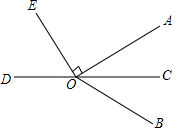 A、63° B、33° C、28° D、27°
A、63° B、33° C、28° D、27°二、填空题
-
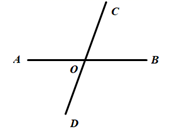
11. 比较大小: 38°15'38.15° (选填“>”“<”“=”).12. 如图,直线AB,CD交于点O, ,现作射线OE⊥CD,则∠AOE的大小为.
 13. 如图所示的网格是正方形网格, 是网格线的交点,则 与 的大小关系为: (填“>”,“=”或“<”).
13. 如图所示的网格是正方形网格, 是网格线的交点,则 与 的大小关系为: (填“>”,“=”或“<”).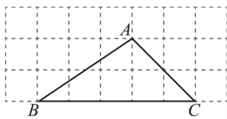 14. 比较两个角 和 的大小关系:小明用度量法测得 ;小丽采用叠合法比较这两个角的大小,她将 和 的顶点重合,边 与 重合,边 和 置于重合边的同侧,则边 .(填序号:①“在 的内部”;②“在 的外部”;③“与边 重合”)15. 如图所示的网格是正方形网格, (填“>”,“=”或“<”)
14. 比较两个角 和 的大小关系:小明用度量法测得 ;小丽采用叠合法比较这两个角的大小,她将 和 的顶点重合,边 与 重合,边 和 置于重合边的同侧,则边 .(填序号:①“在 的内部”;②“在 的外部”;③“与边 重合”)15. 如图所示的网格是正方形网格, (填“>”,“=”或“<”) 16. 已知射线OA,从O点再引射线OB,OC,使∠AOB=67°31′,∠BOC=48°39′,则∠AOC的度数为
16. 已知射线OA,从O点再引射线OB,OC,使∠AOB=67°31′,∠BOC=48°39′,则∠AOC的度数为三、解答题
-
17. 如图,已知 平分 ,求 的度数.
 18. 如图,点O在直线AB上,OM平分∠AOC,ON平分∠BOC,如果∠1:∠2=1:2,求∠1的度数.
18. 如图,点O在直线AB上,OM平分∠AOC,ON平分∠BOC,如果∠1:∠2=1:2,求∠1的度数. 19.
19.如图,已知同一平面内,∠AOB=90゜,∠AOC=60゜.
(1) 求∠COB ;
(2)如OD平分∠BOC,OE平分∠AOC,直接写出∠DOE的度数为 ;
(3)试问在(2)的条件下,如果将题目中∠AOC=60゜改成∠AOC=2α(α<45゜),其他条件不变,你能求出∠DOE的度数吗?若能,请你写出求解过程;若不能,请说明理由.
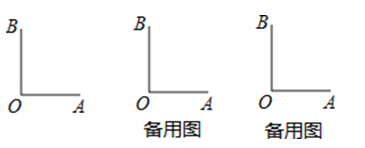 20. 如图①,已知OC是∠AOB内部的一条射线,M、N分别为OA、OB上的点,线段OM、ON同时开始旋转,线段OM以30度/秒绕点O逆时针旋转,线段ON以10度/秒的速度绕点O顺时针旋转,当OM旋转到与OB重合时,线段OM、ON都停止旋转.设OM的旋转时间为t秒.
20. 如图①,已知OC是∠AOB内部的一条射线,M、N分别为OA、OB上的点,线段OM、ON同时开始旋转,线段OM以30度/秒绕点O逆时针旋转,线段ON以10度/秒的速度绕点O顺时针旋转,当OM旋转到与OB重合时,线段OM、ON都停止旋转.设OM的旋转时间为t秒.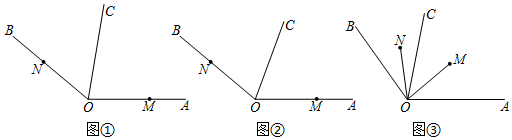 (1)、若∠AOB=140°,当t=2秒时,∠MON= , 当t=4秒时,∠MON=;(2)、如图②,若∠AOB=140°,OC是∠AOB的平分线,求t为何值时,两个角∠NOB与∠COM中的其中一个角是另一个角的2倍.(3)、如图③,若OM、ON分别在∠AOC、∠COB内部旋转时,总有∠COM=3∠CON,请直接写出 的值.21. 已知,直线AB与直线CD相交于O,OB平分∠DOF.
(1)、若∠AOB=140°,当t=2秒时,∠MON= , 当t=4秒时,∠MON=;(2)、如图②,若∠AOB=140°,OC是∠AOB的平分线,求t为何值时,两个角∠NOB与∠COM中的其中一个角是另一个角的2倍.(3)、如图③,若OM、ON分别在∠AOC、∠COB内部旋转时,总有∠COM=3∠CON,请直接写出 的值.21. 已知,直线AB与直线CD相交于O,OB平分∠DOF. (1)、如图,若∠BOF=40°,求∠AOC的度数;(2)、作射线OE,使得∠COE=60°,若∠BOF=x°( ),求∠AOE的度数(用含x的代数式表示).
(1)、如图,若∠BOF=40°,求∠AOC的度数;(2)、作射线OE,使得∠COE=60°,若∠BOF=x°( ),求∠AOE的度数(用含x的代数式表示).