云南省玉溪市峨山彝族自治县2020-2021学年七年级上学期数学期末试卷
试卷更新日期:2021-10-13 类型:期末考试
一、填空题
-
1. -5的倒数是2. 地球上的海洋面积约为361000000km2 , 则科学记数法可表示为 km2 .3. 单项式 的系数是 ,次数是 .4. 当m =时,关于 的方程 是一元一次方程.5. 几个人共同种一批树苗,如果每人种10棵,则剩下6棵树苗未种,如果每人种12棵,则缺6棵树苗,用x表示参加种树的人数,则可列出一元一次方程.6. 如图所示,把一根绳子对折成AB,从P处把绳子剪断,已知AP= PB,若剪断后的各段绳子中最长的一段为60㎝,则绳子的原长为 .

二、单选题
-
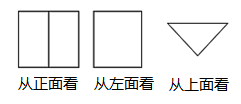
7. 峨山县某超市出售真空小包装火腿,每包以标准克数(450克)为基数,超过的克数记作正数,不足的克数记作负数,以下数据是记录结果,其中表示实际克数最接近标准克数的是( )A、+2 B、-3 C、-1 D、+48. 从正面、左面、上面观察一个几何体,得到的平面图形如图,则这个几何体是( )
 A、
A、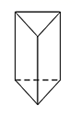 B、
B、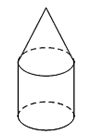 C、
C、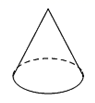 D、
D、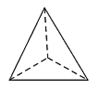 9. 下列计算正确的是( )A、 B、 C、 D、10. 下列各个选项中的两个单项式,不是同类项的是( )A、 与 B、 与 C、 与 D、π与-311. 如图,将一副三角板叠放在一起,使直角顶点重合于C点,且∠ECD=41°,则∠ACB=( )
9. 下列计算正确的是( )A、 B、 C、 D、10. 下列各个选项中的两个单项式,不是同类项的是( )A、 与 B、 与 C、 与 D、π与-311. 如图,将一副三角板叠放在一起,使直角顶点重合于C点,且∠ECD=41°,则∠ACB=( )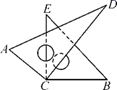 A、138° B、139° C、140° D、141°12. 如图,若点 , , 所对应的数为 , , ,则下列大小关系错误的是( )
A、138° B、139° C、140° D、141°12. 如图,若点 , , 所对应的数为 , , ,则下列大小关系错误的是( ) A、 B、-a<b<c C、b<-c<a D、a<c<-b13. 在一次猜谜抢答赛上,每人需要回答30道题目,答对1题加20分,答错1题扣10分,小明共得了120分,设小明答对了 道题.根据题意列出的方程正确的是( )A、 B、 C、 D、14. 在计算机程序中,二叉树是一种表示数据结构的方法,如图,一层二叉树的结点总数为1,二层二叉树的结点总数为3,三层二叉树的结点总数为7,……,照此规律,八层二叉树的结点总数为 ( )
A、 B、-a<b<c C、b<-c<a D、a<c<-b13. 在一次猜谜抢答赛上,每人需要回答30道题目,答对1题加20分,答错1题扣10分,小明共得了120分,设小明答对了 道题.根据题意列出的方程正确的是( )A、 B、 C、 D、14. 在计算机程序中,二叉树是一种表示数据结构的方法,如图,一层二叉树的结点总数为1,二层二叉树的结点总数为3,三层二叉树的结点总数为7,……,照此规律,八层二叉树的结点总数为 ( )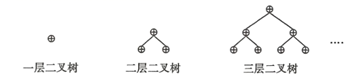 A、126 B、255 C、127 D、256
A、126 B、255 C、127 D、256三、解答题
-
15. 计算: .16. 解方程: .17. 先化简,再求值: ,其中 .18. 如图,已知B、C两点把线段AD分成2:4:3的三部分,M是AD的中点,若CD=6,求线段AD和MC的长.
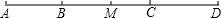 19. 某一出租车一天下午以鼓楼为出发地在东西方向营运,向东走为正,向西走为负,行车里程(单们:)依先后次序记录如下:+9,﹣3,﹣5,+4,﹣8,+6,﹣3,﹣6,﹣4,+10(1)、将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?(2)、若每千米的价格为3元,司机一个下午的营业额是多少?20. 如图,将边长为m的正方形纸板沿虚线剪成两个小正方形和两个长方形,拿掉边长为n的小正方形纸板后,将剩下的三块拼成新的长方形.
19. 某一出租车一天下午以鼓楼为出发地在东西方向营运,向东走为正,向西走为负,行车里程(单们:)依先后次序记录如下:+9,﹣3,﹣5,+4,﹣8,+6,﹣3,﹣6,﹣4,+10(1)、将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?(2)、若每千米的价格为3元,司机一个下午的营业额是多少?20. 如图,将边长为m的正方形纸板沿虚线剪成两个小正方形和两个长方形,拿掉边长为n的小正方形纸板后,将剩下的三块拼成新的长方形.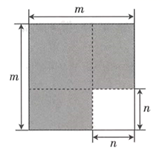 (1)、用含m,n的式子表示新长方形的周长.(2)、若m=10,n=4,求新长方形的面积.21. 如图,已知O是直线AB上一点,∠AOC=140°,OD平分∠AOC,∠DOE=90°.
(1)、用含m,n的式子表示新长方形的周长.(2)、若m=10,n=4,求新长方形的面积.21. 如图,已知O是直线AB上一点,∠AOC=140°,OD平分∠AOC,∠DOE=90°. (1)、求∠BOD的度数.(2)、通过计算判断OE是否平分∠BOC.22. 近年来,随着人类社会的发展,人们对水的需求量越来越大,很多地方出现了用水紧张的情况.为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费;超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按b元收费.该市某户今年4,5月份的用水量和所交水费如下表所示:
(1)、求∠BOD的度数.(2)、通过计算判断OE是否平分∠BOC.22. 近年来,随着人类社会的发展,人们对水的需求量越来越大,很多地方出现了用水紧张的情况.为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费;超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按b元收费.该市某户今年4,5月份的用水量和所交水费如下表所示:月份
用水量(立方米)
收费(元)
4
5
10
5
9
22.5
设某户每月用水量为x(立方米).
(1)、求a,b的值;(2)、当x>6时,请用含x的式子表示出用户应该缴纳的水费;(3)、若该户6月份水费为33元,则该用户6月份用水量是多少立方米?23. 如图,已知数轴上点O为原点,A、B两点所表示数分别为﹣2和8.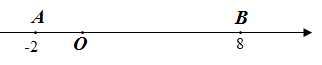 (1)、线段AB的长为;(2)、动点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒,
(1)、线段AB的长为;(2)、动点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒,①当0<t<10时,PA= , PB= , 点P表示的数为;
(3)、②若点M是线段PA的中点,点N是线段PB的中点,试判断线段MN的长度是否与点P的运动时间t有关.若有关,请求出线段MN的长度与t的关系式;若无关,请说明理由,并求出线段MN的长度.