山西省运城市盐湖区2020-2021学年七年级上学期数学期末试卷

试卷更新日期：2021-10-13 类型：期末考试

进入出卷网下载

一、单选题

1. 2020年12月15日运城市天气预报，盐湖区当日气温是 $- 3$ ℃～5℃，则这天的温差（最高气温减最低气温，单位：℃）是（）

A、8 B、2 C、 $- 2$ D、 $- 8$

查看试题解析
2. 下列运算正确的是（）

A、3a＋2a＝ $5 a^{2}$ B、 $2 a^{2} b - a^{2} b = a^{2} b$ C、3a＋3b＝3ab D、 $g^{5} - g^{2} = g^{3}$

查看试题解析
3. 2020年12月17日，嫦娥五号返回器携带月球样品从距离地球384000千米远的月球安全回家，标志着我国探月工程“绕、落、回”三步走规划如期完成．其中384000用科学记数法可表示为（）

A、 $3.84 \times 10^{4}$ B、 $38.4 \times 10^{4}$ C、 $3.84 \times 10^{5}$ D、 $3.84 \times 10^{6}$

查看试题解析
4. 由6个相同的小正方体搭成的几何体如图所示，则它从正面看到的视图是（）

A、 B、 C、 D、

查看试题解析
5. 下列调查中，适宜采用普查方式的是（）

A、调查一批新型节能灯泡的使用寿命 B、调查全市中学生观看《夺冠》的情况 C、调查运城市中小学生的课外阅读时间 D、对长征五号遥五运载火箭零部件质量情况的调查

查看试题解析
6. 已知点P是 $C D$ 中点，则下列等式中：① $P C = P D$ ；② $P C = \frac{1}{2} C D$ ；③ $C D = 2 P D$ ；④ $P C + P D = C D$ ；正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 按如图的程序计算，若开始输入的值x为正整数，当输入x＝10时，输出的值为（）

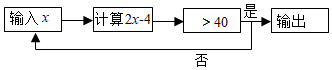A、28 B、52 C、56 D、100

查看试题解析
8. “双十一”期间，某电商决定对网上销售的某种服装按成本价提高40%后标价，又以8折（即按标价的80%）优惠卖出，结果每件服装仍可获利21元，则这种服装每件的成本是（）

A、160元 B、175元 C、170元 D、165元

查看试题解析
9. 如图，将一个三角板 $60 °$ 角的顶点与另一个三角板的直角顶点重合， $∠ 1 = 28 ° ， ∠ 2$ 的大小是（）

A、 $28 °$ B、 $32 °$ C、 $58 °$ D、 $62 °$

查看试题解析
10. 中国古代入民很早就在生产生活中发现了许多有趣的数学问题，其中《孙子算经》中有个问题：今有四人共车，一车空；二人共车，八人步，问人与车各几何？这道题的意思是：今有若干人乘车，每4人乘一车，最终剩余1辆车，若每2人共乘一车，最终剩余8个人无车可乘，问有多少人，多少辆车？如果我们设有x辆车，则可列方程（）

A、 $4 (x - 1) = 2 x + 8$ B、 $4 (x + 1) = 2 x - 8$ C、 $\frac{x}{4} + 1 = \frac{x + 8}{2}$ D、 $\frac{x}{4} - 1 = \frac{x - 8}{2}$

查看试题解析

二、填空题

11. 东、西为两个相反方向，若+2米表示向东运动2米，那么向西运动7米记为米．

查看试题解析
12. $A$ 、 $B$ 两地之间弯曲的公路改直，能够缩短路程，其根据的道理是.

查看试题解析
13. 归纳“T”字形，用棋子摆成的“T”字形如图所示，按照图①，图②，图③的规律摆下去，摆成第n个“T”字形需要的棋子个数为．

查看试题解析
14. 一个几何体由一些大小相同的小正方体搭成，从正面和左面看到的这个几何体的形状如图所示，则搭成该几何体的小正方体的个数最少是．

查看试题解析
15. 点C在线段 $A B$ 上，共有三条线段 $A B$ 、 $A C$ 和 $B C$ ，若其中有一条线段的长度是另外一条线段长度的2倍，则称点C是线段 $A B$ 的“巧点”，若 $A B = 15$ ，点C是线段 $A B$ 的“巧点”，则 $A C$ 的长是．

查看试题解析

三、解答题

16.

(1)、 $- 2^{3} - 4 \div (- \frac{1}{3}) + 2 \times {(- 3)}^{2}$ ；

(2)、 $(- 12) \times (\frac{1}{4} - \frac{1}{3} - \frac{1}{12})$ ．

查看试题解析
17. 解方程：

(1)、 $5 x + 4 = 3 (x - 4)$

(2)、 $\frac{4 x - 3}{5} - 1 = \frac{2 x - 2}{3}$

查看试题解析
18. 先化简，再求值： $5 y^{2} - x^{2} + 3 (2 x^{2} - 3 x y) - 5 (x^{2} + y^{2})$ 的值，其中 $x = 1$ ， $y = - 2$ .

查看试题解析
19. 为防止2020年下半年新冠疫情反复，运城市盐湖区某中学就全体初中学生对新冠肺炎疫情防控知识的了解程度进行了一次抽样调查统计，下图是采集数据后绘制的两幅不完整的统计图（A：不了解，B：一般了解，C：了解较多，D：熟悉）．请你根据图中提供的信息回答以下问题：

(1)、这次被调查的学生共有多少人？

(2)、补全条形统计图．

(3)、求出扇形统计图中“了解较多”部分所对应的圆心角度数．

(4)、该中学初中共有1200名学生，估计对疫情防控知识了解程度为“熟悉”的学生大约有多少？

查看试题解析
20. 根据要求，解答下列问题．
依照下列解方程 $\frac{0.2 x + 0.1}{0.3} - \frac{10 x + 1}{6} = 1$ 的过程，请在前面的括号内填写变形步骤，在后面的括号内填写变形依据．

解：原方程可变形为 $\frac{2 x + 1}{3} - \frac{10 x + 1}{6} = 1$ （分数的基本性质）

去分母，得 $2 (2 x + 1) - (10 x + 1) = 6$ （    ①    ）

（    ②    ），得 $4 x + 2 - 10 x - 1 = 6$ （乘法分配律）

移项，得 $4 x - 10 x = 6 - 2 + 1$ （    ③    ）

（    ④    ）得 $- 6 x = 5$ （合并同类项法则）

系数化为1．得 $x = - \frac{5}{6}$

查看试题解析
21. 阅读材料，解答下面问题．
无限循环小数化分数：利用一元一次方程可以将任何一个无限循环小数化成分数形式．下面以 $0. \dot{6}$ 为例说明：

设 $x = 0. \dot{6}$ ①，

由 $0. \dot{6} = 0.666 \cdot \cdot \cdot$ ．

可得 $10 x = 6.666 \cdot \cdot \cdot$ ②，

由②-①，得 $10 x - x = 6$

解得： $x = \frac{2}{3}$ ，所以， $0. \dot{6} = \frac{2}{3}$

模仿：

(1)、将无限循环小数 $0. \dot{7}$ 化成分数形式．

(2)、 $0. \dot{1} \dot{2} =$ ．（直接写出答案）

查看试题解析
22. 春节期间，七（1）班的李平、王丽等同学随家长一同到某公园游玩，下面是购买门票时，李平与他爸爸的对话（如图），试根据图中的信息，解答下列问题：

(1)、李平他们一共去了几个成人，几个学生？

(2)、请你帮助算一算，用哪种方式购票更省钱？说明理由．

(3)、购完票后，李平发现七（2）班的张明等8名同学和他们的12名家长共20人也来购票，请你为他们设计出最省的购票方案，并求出此时的购票费用.

查看试题解析
23. 综合与实践
问题情境：在数学活动课上，老师和同学们以“线段与角的共性”为主题开展数学活动，发现线段的中点的概念与角的平分线的概念类似，甚至它们在计算的方法上也有类似之处，它们之间的题目可以转换，解法可以互相借鉴．

(1)、问题探究：
①如图1，点C在线段 $A B$ 上， $A B = 14 cm ， A C = 8 cm$ ，点M、N分别是线段 $A C$ 、 $B C$ 的中点．求线段 $M N$ 的长；

②善于思考的小聪发现：只要点C在线段 $A B$ 上，任意改变点C的位置，其他条件不变， $M N$ 的长就是 $\frac{1}{2} A B$ ．小聪理由如下：因为M、N分别是线段 $A C$ 、 $B C$ 的中点，所以 $M C = \frac{1}{2} A C ， C N = \frac{1}{2} B C$ ，所以 $M N = M C + N C = \frac{1}{2} A C + \frac{1}{2} B C = \frac{1}{2} (A C + B C) = \frac{1}{2} A B$ ．老师肯定了小聪的方法．

(2)、继续探究：
①如图2， $∠ A O B$ 是直角，射线 $O C$ 在 $∠ A O B$ 内部，且 $∠ A O C = 30 ° ， O N$ 是 $∠ A O C$ 的平分线， $O M$ 是 $∠ B O C$ 的平分线，则 $∠ M O N =$ $°$ ．（直接写出结果）

②如图2， $∠ A O B$ 是直角，射线 $O C$ 在 $∠ A O B$ 内部，且 $∠ A O C$ 是锐角， $O N$ 是 $∠ A O C$ 的平分线， $O M$ 是 $∠ B O C$ 的平分线．当 $∠ A O C$ 的大小发生改变时， $∠ M O N$ 的大小也会发生改变吗？如果不变，求出 $∠ M O N$ 的度数；如果改变，请说明理由．（类比小聪的方法）

(3)、深入探究：
如图3，若 $∠ A O B = n °$ ，在角的外部作射线 $O C$ ，再分别作 $∠ A O C$ 和 $∠ B O C$ 的角平分线 $O N$ 、 $O M$ ．若 $∠ A O C = m °$ ，则 $∠ M O N =$ $°$ ．（直接写出结果）

查看试题解析