山西省太原市清徐县2020-2021学年七年级上学期数学期末试卷
试卷更新日期:2021-10-13 类型:期末考试
一、单选题
-
1. 有理数2021的相反数为( )A、2021 B、-2021 C、 D、2. 下列调查中,最适合采用普查方式的是( )A、调查太原市民平均每日废弃口罩的数量 B、调查某一批次LED灯泡的使用寿命 C、调查嫦娥五号零部件的合格情况 D、调查全国中小学生对央视一套播出的电视剧《跨过鸭绿江》的收视率3. 如图的几何体由6个相同的小正方体组成,从它的左面看到的平面图形是( )
 A、
A、 B、
B、 C、
C、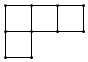 D、
D、 4. 下列计算一定正确的是( )A、 B、 C、 D、5. 2020年末“霸王级”寒潮来袭,全国各地气温骤降,如图表示2021年元月某天山西省四个城市的天气情况.这一天最高气温最低的城市为( )
4. 下列计算一定正确的是( )A、 B、 C、 D、5. 2020年末“霸王级”寒潮来袭,全国各地气温骤降,如图表示2021年元月某天山西省四个城市的天气情况.这一天最高气温最低的城市为( ) A、大同 B、太原 C、长治 D、晋城6. 人民网北京2021年1月7日电,截至1月3日6时,我国首次火星探测任务天问一号火星探测器已经在轨飞行约163天,飞行里程突破4亿公里,距离地球接近1.3亿公里,距离火星约830万公里.数据830万公里用科学记数法表示为( )
A、大同 B、太原 C、长治 D、晋城6. 人民网北京2021年1月7日电,截至1月3日6时,我国首次火星探测任务天问一号火星探测器已经在轨飞行约163天,飞行里程突破4亿公里,距离地球接近1.3亿公里,距离火星约830万公里.数据830万公里用科学记数法表示为( ) A、8.3×106公里 B、8.3×105公里 C、8.3×104公里 D、0.83×106公里7. 下列四个图中,能用∠1、∠AOB、∠O三种方法表示同一个角的是( )A、
A、8.3×106公里 B、8.3×105公里 C、8.3×104公里 D、0.83×106公里7. 下列四个图中,能用∠1、∠AOB、∠O三种方法表示同一个角的是( )A、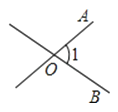 B、
B、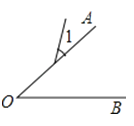 C、
C、 D、
D、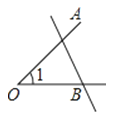 8. 小颖在研究无盖的正方体盒子的展开图时,画出下面4个展开图,其中符合要求的共有( )
8. 小颖在研究无盖的正方体盒子的展开图时,画出下面4个展开图,其中符合要求的共有( ) A、1个 B、2个 C、3个 D、4个9. 随着我国高铁技术的不断成熟和发展,高铁已成为重要的“中国名片”,领跑世界.如图是我国交通运输部2020年1月统计的“2014年~2019年期间中国高铁运营里程及其增长情况的统计图”.根据统计图得出如下结论,其中错误的是( )
A、1个 B、2个 C、3个 D、4个9. 随着我国高铁技术的不断成熟和发展,高铁已成为重要的“中国名片”,领跑世界.如图是我国交通运输部2020年1月统计的“2014年~2019年期间中国高铁运营里程及其增长情况的统计图”.根据统计图得出如下结论,其中错误的是( ) A、2014年~2019年期间中国高铁运营里程逐年增长 B、2014年~2019年期间中国高铁运营里程先减后增 C、2014年~2019年期间2019年中国高铁运营里程增长率最高 D、2014年~2019年期间2017年中国高铁运营里程增长率最低10. 《孙子算经》中有一道题,原文是:今有三人共车,二车空:二人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车:若每2人共乘一车,最终剩余9个人无车可乘,问共有多少人,多少辆车?设共有x人,可列方程( )A、 B、 C、 D、
A、2014年~2019年期间中国高铁运营里程逐年增长 B、2014年~2019年期间中国高铁运营里程先减后增 C、2014年~2019年期间2019年中国高铁运营里程增长率最高 D、2014年~2019年期间2017年中国高铁运营里程增长率最低10. 《孙子算经》中有一道题,原文是:今有三人共车,二车空:二人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车:若每2人共乘一车,最终剩余9个人无车可乘,问共有多少人,多少辆车?设共有x人,可列方程( )A、 B、 C、 D、二、填空题
-
11. 方程2x+▲=3x,▲处是被墨水盖住的常数,已知方程的解是x=2,那么▲处的常数是 .12. 如图,经过刨平的木板上的 , 两个点,可以弹出一条笔直的墨线.这个方法依据的数学原理是 .
 13. 某店铺举行2021“元旦”大促销活动,将一批进价为50元/只的书包打八折销售,希望每只书包仍可获利10元,则销售这批书包时的标价应是元/只.14. 下面是一组有规律的算式,根据其中规律,第 个算式为: .
13. 某店铺举行2021“元旦”大促销活动,将一批进价为50元/只的书包打八折销售,希望每只书包仍可获利10元,则销售这批书包时的标价应是元/只.14. 下面是一组有规律的算式,根据其中规律,第 个算式为: .第l个算式: ;第2个算式: ;第3个算式: ;第4个算式: ;…
15. 如图,射线 , , 均在 内部,且 . 平分 , 平分 .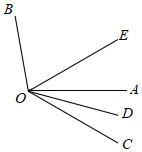
请从A,B两题中任选一题作答.我选择 .
A.若 , ,则 的度数为 .
B.若 ,则 的度数为 .(用含 的式子表示)
三、解答题
-
16. 计算:(1)、 ;(2)、 .17. 先化简再求值: ,其中 , .18. 下面是小彬同学解一元一次方程的过程,请认真阅读并完成相应任务.
解方程: .
解:……,得 . ……第一步
去括号,得 . ……第二步
移项,得 . ……第三步
合并同类项,得 . ……第四步
方程两边同除以2,得 . ……第五步
填空:
(1)、以上求解步骤中,第一步进行的是 , 这一步的依据是;(2)、以上求解步骤中,第步开始出现不符合题意,具体的不符合题意是;(3)、该方程正确的解为 .19. 如图,在平面内有三个点 , , . (1)、按下面的要求作图:(要求:利用尺规,不写画法,保留作图痕迹,不写结论)
(1)、按下面的要求作图:(要求:利用尺规,不写画法,保留作图痕迹,不写结论)①连接 , ,作射线 ;
②在射线 上作线段 ,使 .
(2)、已知 , ,点 是 的中点.将点 标在(1)所画的图中,并求线段 的长.20. 阅读是人们认识世界、获取信息的重要方法.脑科学研究表明“10-16岁是阅读能力和阅读质量提升的关键期”,某校为提升学生的阅读能力,培养阅读习惯,向全体学生发出了“让读书成为一种习惯”的活动倡议.收集数据:小明利用如图所示的调查问卷随机调查了50名同学,得到他们最近一周课外阅读总时间的数据,如下:

整理分析:李老师帮他整理了这组数据,并绘制了如下的频数直方图和扇形统计图.
 (1)、请将频数直方图和扇形统计图中空缺的部分补充完整;(2)、试说明这组数据的分布特点:;(写出一条即可)(3)、问题解决:
(1)、请将频数直方图和扇形统计图中空缺的部分补充完整;(2)、试说明这组数据的分布特点:;(写出一条即可)(3)、问题解决:已知该校共有学生2000人,请根据调查数据估计:该校全体学生中最近一周课外阅读总时长不足3小时的有多少人?
21. 随着地铁2号线一期的开通,太原正式进入地铁时代.地铁2号线一期采用按里程分段计价的票制,全程最高票价为6元,学生可享受半价.周日,七年级某班师生共36人从始发站“西桥”乘地铁至终点站“尖草坪”;感受“地铁速度”,其中所有的学生享受了半价票,教师均买全价票,单程共付车票费用126元.参加本次活动的师生各多少人? 22. 观察下列表格中两个代数式及其相应的值,回答问题:
22. 观察下列表格中两个代数式及其相应的值,回答问题:x
…
-2
-1
0
1
2
…
…
9
7
5
3
…
…
-11
-9
-7
-5
…
(1)、(初步感知)根据表中信息可知: ; ;
(2)、(归纳规律)表中 的值的变化规律是: 的值每增加1, 的值就都减少2.类似地, 的值的变化规律是:;
(3)、(问题解决)请从A,B两题中任选一题作答.我选择( )题.
A.根据表格反应的变化规律,当 ( )时, 的值大于 的值.
B.请直接写出一个含 的代数式,要求 的值每增加1,代数式的值就都减小5,且当 时,代数式的值为-7.
23. 综合与实践问题情境:
太原环城旅游公路暨公路自行车赛道环西山而建,全长136千米,将百余处景点串连成一条线,同时,也是山西首条自行车专用赛道.周日,某自行车骑行团在该赛道组织骑行活动,甲、乙、丙三人参加了这次活动.甲从赛道一端(记为A)出发向另一端(记为B)骑行,甲出发40分钟时乙从赛道B端出发,二人相向而行.已知甲的平均速度为50千米/时,乙的平均速度为30千米/时.设甲骑行的时间为 小时,请解决下列问题.
 (1)、建立模型:
(1)、建立模型:在甲从赛道A端到B端骑行过程中,用含 的代数式表示:
甲离开A端的赛程为千米,乙离开B端的赛程为千米;
(2)、问题解决:当甲、乙二人相遇时, 的值为;
(3)、乙出发20分钟时,丙从B端出发向A端骑行,平均速度也为30千米/时.请从A,B两题中任选一题作答.我选择题.
A.若甲到达B端后停止骑行,丙到A端后也停止骑行,当甲与丙之间相距的赛程恰好为6千米时,求 的值;
B.若甲骑行至离B端16千米时立刻掉头向A端骑行,则在乙、丙到达A端之前,甲是否能追上乙、丙?若能追上,分别求追上乙、丙时 的值;若不能,请说明理由.