山西省吕梁市兴县2020-2021学年七年级上学期数学期末试卷

试卷更新日期：2021-10-13 类型：期末考试

进入出卷网下载

一、单选题

1. 下图中表示∠ABC的图是（）

A、 B、 C、 D、

查看试题解析
2. 若关于 $x$ 的方程 $2 x + a - 4 = 0$ 的解是 $x = - 2$ ，则 $a$ 的值是（）

A、 $- 8$ B、0 C、8 D、4

查看试题解析
3. 从下列物体抽象出来的几何图形可以看成圆柱的是（）

A、 B、 C、 D、

查看试题解析
4. 下列说法正确的是（）

A、字母 $a$ 和数字1都不是单项式 B、单项式 $x y z$ 的次数是3 C、 $\frac{3}{x}$ 是单项式 D、 $- \frac{2 x^{3} y}{3}$ 这个单项式系数是2

查看试题解析
5. 在下列变形中，正确的是（）

A、如果a=b ，那么 $\frac{a}{3} = \frac{b}{3}$ B、如果 $\frac{a}{2}$ =4，那么a=2 C、如果a–b+c=0，那么a=b+c D、如果a=b ，那么a+c=b–c

查看试题解析
6. 魔术师在小丽面前对她说：
魔术师：请你在纸上任意写一个数字，不要让我看到；

魔术师：将你写的数字乘以6，然后加9，所得结果再除以3，最后再减去一开始你写的数字的2倍，得到一个答案；

魔术师：无论你写哪个数字，我都能猜中你算出来的答案．

假设小丽所写数字为 $m$ ，那么魔术师猜中的结果应为（）

A、2 B、3 C、4 D、 $a + 4$

查看试题解析
7. 下列计算中，正确的是（）．

A、 $| - 15 | = - 15$ B、 $4.5 - 1.7 - 2.5 + 1.8 = 5.5$ C、 $- (- 2) = 2$ D、 $- \frac{1}{3} \div (- 3) = 1$

查看试题解析
8. 根据语句点 $M$ 在直线 $a$ 外，过 $M$ 有一直线 $b$ 交直线 $a$ 于点 $N$ 、直线 $b$ 上另一点 $Q$ 位于 $M$ 、 $N$ 之间画图，正确的是（）

A、 B、 C、 D、

查看试题解析
9. 数轴上的点 $M$ 距原点5个单位长度，将点 $M$ 向右移动3个单位长度至点 $N$ ，则点 $N$ 表示的数是（）

A、8 B、2 C、 $- 8$ 或2 D、8或 $- 2$

查看试题解析
10. 甲乙两人各用一张正方形的纸片ABCD折出一个45°的角（如图），两人做法如下：
甲：将纸片沿对角线AC折叠，使B点落在D点上，则∠1=45°；
乙：将纸片沿AM、AN折叠，分别使B、D落在对角线AC上的一点P，则∠MAN=45°．
对于两人的做法，下列判断正确的是（）

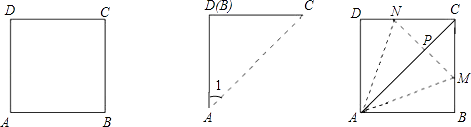A、甲乙都对 B、甲对乙错 C、甲错乙对 D、甲乙都错

查看试题解析

二、填空题

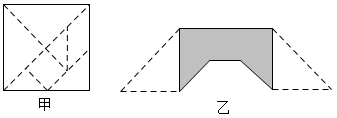
11. 对单项式“ $0.75 m$ ”可以解释为：一件商品原价 $m$ 元，若按原价的七五折出售，这件商品现在的售价为 $0.75 m$ 元．某超市的苹果价格为39元/斤，则代数式“ $50 - 3.9 x$ ”可表示的实际意义．

查看试题解析
12. 七巧板是一种古老的中国传统智力玩具，顾名思义，是由七块板组成的．清陆以潘《冷庐杂识》卷一中写道：近又有七巧图，其式五，其数七，其变化之式多至千余．玩家也可以把它拼成各种人物、形象、动物、桥、房、塔等等．小明用一块边长为 $8 c m$ 的正方形的厚纸板，做了一套七巧板（如图甲）．小聪用小明做的七巧板拼成一座桥（如图乙），这座桥的阴影部分的面积是．

查看试题解析
13. 2的相反数是 $- 2$ ，则 $2 + (- 2) = 0$ ：0的相反数是0，则 $0 + 0 = 0$ ； $- 1$ 的相反数是1，则 $(- 1) + 1 = 0$ ，故若 $a$ ， $b$ 互为相反数，则 $a + b = 0$ ；反之若 $a + b = 0$ ，则 $a$ ， $b$ 互为相反数．说明了；相反，．（用文字叙述）

查看试题解析
14. 学习强国平台报：2020年12月20日，新华记者从山西省扶贫办了解到，自2018年以来，山西认定2294个扶贫产品，借助“五进九销”累计销售贫困地区农产品88亿元，带动24.22万贫困人口增收．其中88亿用科学记数法表示为．

查看试题解析
15. 欧拉是一位著名的数学家，他把他的一生都献给了人类的数学事业，在他一生岁数的 $\frac{1}{4}$ 那年，他发表了第一篇数学论文，并且获得了巴黎科学院奖金，此后过了7年，他成为彼得堡科学院的数学教授，在欧拉去世的前17年，他不幸双目失明了，但他继续在黑暗的世界里凭着他的记忆和心算进行数学研究，在这17年里，他写出了数学论文400篇，正好是他一生的岁数与他成为彼得堡学院数学教授时岁数之差的8倍．根据以上信息，请你算出数学家欧拉一生岁．

查看试题解析

三、解答题

16. 题目：化简： $x + 3 y + 6 x + 4 y - 7 x + 5 z$ ．
下面是小马虎的解题过程：

解： $x + 3 y + 6 x + 4 y - 7 x - 5 z$

$= (3 y + 4 y) + (x + 6 x - 7 x) - 5 z$ ①

$= 7 y + 14 x - 5 z$ ．②

请问小马虎的解题过程是从哪一步开始出错的？第①步的解题依据是什么？请写出正确的解题过程．

查看试题解析
17. 垃圾打捞船 $A$ 和 $B$ 都停驻在湖边观测湖面，从 $A$ 船发现它的北偏东60°方向有白色漂浮物，同时，从 $B$ 船也发现该白色漂浮物在它的北偏西45°方向．

(1)、试在图中确定白色漂浮物 $C$ 的位置；

(2)、点 $C$ 在点 $A$ 的北偏东60°的方向上，那么点 $A$ 在点 $C$ 的______方向上．

A、南偏东30° B、南偏西30° C、南偏东60° D、南偏西60°

(3)、猜想 $∠ A C B$ 度数为．

查看试题解析
18. 计算：

(1)、 $- 3^{2} - {(- 2)}^{2} \times | - \frac{1}{2} |$ ，

(2)、 $35 ° 1 6^{'} \times 5$ ．

查看试题解析
19. 解方程：

(1)、 $- 3 x + 4 = x - 8$ ；

(2)、 $- 1 + \frac{x - 2}{2} = \frac{- 3 x + 1}{8}$ ．

查看试题解析
20. 饺子源于古代的角子，饺子原名“娇耳”，一个饺子皮加馅就可以做一个饺子．中国北方还流行一种面食—合子，含有团团圆圆的美好寓意，在两层饺子皮中间加一层馅，就可以包成一个合子．
“元旦”这天，妈妈走进书房对正在学习的小刚说；“妈妈刚才在厨房包饺子，结果面和多了，做了106个饺子皮，最后包的饺子和合子一共是98个．”小刚说：“妈妈，我能用学过的数学知识列一元一次方程，求出妈妈包的饺子和合子分别是多少．”请你写出小刚的解答过程．

查看试题解析
21. 先阅读下面材料，再完成任务：
（材料）

我们规定：若关于 $x$ 的一元一次方程 $a x = b$ 的解为 $b + a$ ，则称该方程为和解方程．例如；方程 $2 x = - 4$ 的解为 $x = - 2$ ，而 $- 2 = - 4 + 2$ ，则方程 $2 x = - 4$ 为“和解方程”．

（任务）

请根据上述规定解答下列问题：

(1)、关于 $x$ 的一元一次方程 $4 x = - 3$ 是否是“和解方程”；（只写结论）

(2)、已知关于 $x$ 的一元一次方程 $3 x = m$ 是“和解方程”，求 $m$ 的值：

(3)、已知关于 $x$ 的一元一次方程 $- 2 x = m n + n$ 是“和解方程”，并且它的解是 $x = - n$ ，求 $m$ ， $n$ 的值．

查看试题解析
22. 综合与实践
如图，某学校由于经常拔河，长为40米的拔河比赛专用绳AB左右两端各有一段（AC和BD）磨损了，磨损后的麻绳不再符合比赛要求，已知磨损的麻绳总长度不足20米．只利用麻绳AB和一把剪刀（剪刀只用于剪断麻绳）就可以得到一条长20米的拔河比赛专用绳．

七年级的聪聪马上想出一个了办法：在线段 $C D$ 上取一点 $M$ ，使 $C M = C A$ ，对折 $B M$ 找到其中点 $F$ ，将 $A C$ 和 $B F$ 剪掉就得到一条长20米的拔河比赛专用绳 $C F$ ．请你完成下列任务；

(1)、在图中标出点 $M$ 、点 $F$ 的位置；

(2)、判断聪聪剪出的专用绳 $C F$ 是否符合要求．试说明理由．

查看试题解析
23. 综合与探究
某餐厅中1张餐桌可坐6人，如果把多张桌子摆在一起，可以有以下两种摆放方式．

(1)、当有4张桌子时，第一种摆放方式能坐人，第二种摆放方式能坐人；

(2)、当有n张桌子时，第一种摆放方式能坐人，第二种摆放方式能坐人；

(3)、该餐厅有30张这样的长方形桌子，按方式一每3张拼成一张大桌子，则30张桌子可拼成10张大桌子，共可坐人？按方式二呢？

(4)、一天中午，该餐厅来了98名顾客共同就餐客（即桌子要摆在一起），但餐厅中只有25张这样的长方形桌子可用，若你是这家餐厅的经理，你打算选用哪种方式来摆餐桌呢？

查看试题解析