山西省晋中市祁县2020-2021学年七年级上学期数学期末试卷
试卷更新日期:2021-10-13 类型:期末考试
一、单选题
-
1. 下列各数为负数的是( )A、 B、 C、 D、2. 日常生活中,手电筒发射出来的光线,类似于几何中的( )A、折线 B、直线 C、射线 D、线段3. 下列说法正确的是( )A、 是单项式 B、 是三次三项式,常数项是1 C、单项式 的系数是1,次数是0 D、单项式 的次数是2,系数为4. 如图,用一个平面去截正方体,截掉了正方形的一个角,且截面经过原正方体三条棱的中点,剩下几何体的展开图应该是( )
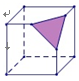 A、
A、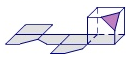 B、
B、 C、
C、 D、
D、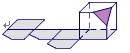 5. 2020年中秋国庆8天小长假结束,由于今年上半年受到新冠疫情影响,人民的旅游热情高度堆积.据文化和旅游部信息显示,八天长假期间,全国共接待国内游客6.37亿人次,按可比口径同比恢复79.0%.实现国内旅游收4543.3亿元,同比恢复69.9%.4543.3亿元用科学用记数法表示为( )元.A、 B、 C、 D、6. 如图,两块直角三角板的直角顶点O重叠在一起,且 恰好平分 ,则 的度数为( )
5. 2020年中秋国庆8天小长假结束,由于今年上半年受到新冠疫情影响,人民的旅游热情高度堆积.据文化和旅游部信息显示,八天长假期间,全国共接待国内游客6.37亿人次,按可比口径同比恢复79.0%.实现国内旅游收4543.3亿元,同比恢复69.9%.4543.3亿元用科学用记数法表示为( )元.A、 B、 C、 D、6. 如图,两块直角三角板的直角顶点O重叠在一起,且 恰好平分 ,则 的度数为( )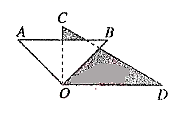 A、 B、 C、 D、7. 以下问题,不适合采用普查方式的是( )A、调查全班同学每月做家务活的时间 B、调查某中学在职教师的身体健康状况 C、对全校同学进行每日体温浏览量统计 D、了解全国初中生“新冠病毒”的知晓程度8. 若代数式 ,则代数式 =( )A、1 B、7 C、9 D、179. 某工厂第一年生产 件产品,第二年比第一年减产了 ,则这两年共生产的产品件数为( )A、 B、 C、 D、10. 如图,点 为线段 外一点,点 , , , 为 上任意四点,连接 , , , ,下列结论错误的是( )
A、 B、 C、 D、7. 以下问题,不适合采用普查方式的是( )A、调查全班同学每月做家务活的时间 B、调查某中学在职教师的身体健康状况 C、对全校同学进行每日体温浏览量统计 D、了解全国初中生“新冠病毒”的知晓程度8. 若代数式 ,则代数式 =( )A、1 B、7 C、9 D、179. 某工厂第一年生产 件产品,第二年比第一年减产了 ,则这两年共生产的产品件数为( )A、 B、 C、 D、10. 如图,点 为线段 外一点,点 , , , 为 上任意四点,连接 , , , ,下列结论错误的是( ) A、以 为顶点的角共有15个 B、若 , ,则 C、若 为 中点, 为 中点,则 D、若 平分 , 平分 , ,则
A、以 为顶点的角共有15个 B、若 , ,则 C、若 为 中点, 为 中点,则 D、若 平分 , 平分 , ,则二、填空题
-
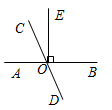
11. 计算: .12. 如图,直线 和 相交于点 , ,如果 ,则 .
 13. 将一条长为 cm的线段延长至 cm,则需要延长 cm.14. 一组“数值转换机”按下面的程序计算,如果输入的数是40,则输出的结果为118,要使输出的结果为172,则输入的最小正整数是 .
13. 将一条长为 cm的线段延长至 cm,则需要延长 cm.14. 一组“数值转换机”按下面的程序计算,如果输入的数是40,则输出的结果为118,要使输出的结果为172,则输入的最小正整数是 . 15. 将长为4,宽为 ( 大于2且小于4)的长方形纸片按如图①所示的方式折叠并压平,剪上一个边长等于长方形宽的正方形,称为第一次操作;再把剩下的长方形按如图②所示的方式折叠并压平,剪下边长等于此时长方形宽的正方形,称为第二次操作;如此反复操作下去…,若在第 次操作后,剩下的长方形恰为正方形,则操作终止.当 时, 的值为 .
15. 将长为4,宽为 ( 大于2且小于4)的长方形纸片按如图①所示的方式折叠并压平,剪上一个边长等于长方形宽的正方形,称为第一次操作;再把剩下的长方形按如图②所示的方式折叠并压平,剪下边长等于此时长方形宽的正方形,称为第二次操作;如此反复操作下去…,若在第 次操作后,剩下的长方形恰为正方形,则操作终止.当 时, 的值为 .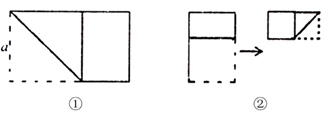
三、解答题
-
16. 计算或化简(1)、(2)、(3)、17. 下面是小彬进行整式化简并求值的过程,请认真阅读并完成相应任务.
,其中 ,
解:原式 第一步
第二步
第三步
以上化简步骤中:
(1)、第一步的依据是;第二步的做法是;第三步的做法是 .(2)、第步开始出现错误,这一步错误的原因是 .(3)、请直接写出该整式化简后的正确结果 , 代入求值得 .18. 解方程(1)、(2)、19. 如图按下列语句画图⑴连接BC.
⑵画直线AB、CD相交于E.
⑶作射线AD.
⑷连接AC、BD,相交于点O.
 20. “停课不停学,学习不延期!”某校为了解疫情期间学生对网课的满意度,采用电子问卷的方式随机调查了部分学生(电子调查表如图所示),并根据调查结果绘制了如下尚不完整的统计图.请根据图中信息回答问题:
20. “停课不停学,学习不延期!”某校为了解疫情期间学生对网课的满意度,采用电子问卷的方式随机调查了部分学生(电子调查表如图所示),并根据调查结果绘制了如下尚不完整的统计图.请根据图中信息回答问题: (1)、本次接受调查的学生共有人;(2)、求选项C的人数,并补全条形统计图;(3)、扇形统计图中,扇形 的圆心角的度数是°;(4)、若该校有1000名学生,请估计满意以上(选择选项A和B)的学生人数多少人?21. 某商场用 元购进 , 两种新型节能台灯共 盏,这两种台灯的进价,标价如下表所示:
(1)、本次接受调查的学生共有人;(2)、求选项C的人数,并补全条形统计图;(3)、扇形统计图中,扇形 的圆心角的度数是°;(4)、若该校有1000名学生,请估计满意以上(选择选项A和B)的学生人数多少人?21. 某商场用 元购进 , 两种新型节能台灯共 盏,这两种台灯的进价,标价如下表所示:类型
型
型
进价(元/盏)
标价(元/盏)
(1)、这两种台灯各购进多少盏?(2)、若 型台灯按标价的 的出售, 型台灯按标价的 折出售,那么这批台灯全部售出后,商场共获利多少元?22. 已知直线AB过点O,∠COD=90°,OE是∠BOC的平分线. (1)、操作发现:①如图1,若∠AOC=40°,则∠DOE=
(1)、操作发现:①如图1,若∠AOC=40°,则∠DOE=②如图1,若∠AOC=α,则∠DOE=(用含α的代数式表示)
(2)、操作探究:将图1中的∠COD绕顶点O顺时针旋转到图2的位置,其他条件不变,②中的结论是否成立?试说明理由.(3)、拓展应用:将图2中的∠COD绕顶点O逆时针旋转到图3的位置,其他条件不变,若∠AOC=α,求∠DOE的度数,(用含α的代数式表示)23. 综合与探究:射线 是 内部的一条射线,若 ,则我们称射线 是射线 的伴随线.例如,如图1, , ,则 ,称射线 是射线 的伴随线;同时,由于 ,称射线 是射线 的伴随线.
完成下列任务:
(1)、如图2, ,射线 是射线 的伴随线,则 ,若 的度数是 ,射线 是射线 的伴随线,射线 是 的平分线,则 的度数是 . (用含 的代数式表示)(2)、如图3,如 ,射线 与射线 重合,并绕点 以每秒 的速度逆时针旋转,射线 与射线 重合,并绕点 以每秒 的速度顺时针旋转,当射线 与射线 重合时,运动停止.①是否存在某个时刻 (秒),使得 的度数是 ,若存在,求出 的值,若不存在,请说明理由;
②当 为多少秒时,射线 , , 中恰好有一条射线是其余两条射线的伴随线.请直接写出结果.