云南省玉溪市江川区2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-10-13 类型:期末考试
一、填空题
-
1. 方程 的根为.2. 如图,已知AB∥CD,若 ,则 = .
 3. 如图,将△ABC绕着点C顺时针旋转一定角度后得到△A′B′C,若∠A=45°.∠B′=110°,则∠ACB的度数是 .
3. 如图,将△ABC绕着点C顺时针旋转一定角度后得到△A′B′C,若∠A=45°.∠B′=110°,则∠ACB的度数是 . 4. 已知点A(1,a)在反比例函数 的图象上,则a的值为 .5. 如图,在⊙O中,A , B , D为⊙O上的点,∠AOB=52°,则∠ADB的度数是 .
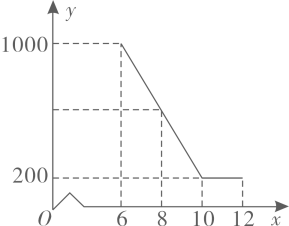
4. 已知点A(1,a)在反比例函数 的图象上,则a的值为 .5. 如图,在⊙O中,A , B , D为⊙O上的点,∠AOB=52°,则∠ADB的度数是 . 6. 如图,一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是 ,则他将铅球推出的距离是m .
6. 如图,一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是 ,则他将铅球推出的距离是m .
二、单选题
-
7. 下列事件为必然事件的是( )A、打开电视,正在播放新闻 B、买一张电影票,座位号是奇数号 C、任意画一个三角形,其内角和是180° D、掷一枚质地均匀的硬币,正面朝上8. 古钱币是我国悠久的历史文化遗产,以下是在《中国古代钱币》特种邮票中选取的部分图形,其中既是轴对称图形又是中心对称图形的是( )
 A、
A、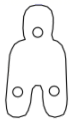 B、
B、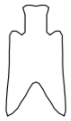 C、
C、 D、
D、 9. 若关于x 的方程(a+1)x2﹣2x﹣1=0 是一元二次方程,则 a 的取值范围是( )A、a≠﹣1 B、a>1 C、a<1 D、a≠010. 如图,MN所在的直线垂直平分线段AB,利用这样的工具,可以找到圆形工件的圆心,如果使用此工具找到圆心,最少使用次数为( ).
9. 若关于x 的方程(a+1)x2﹣2x﹣1=0 是一元二次方程,则 a 的取值范围是( )A、a≠﹣1 B、a>1 C、a<1 D、a≠010. 如图,MN所在的直线垂直平分线段AB,利用这样的工具,可以找到圆形工件的圆心,如果使用此工具找到圆心,最少使用次数为( ). A、1 B、2 C、3 D、411. 已知α、β是一元二次方程x2+x﹣2=0的两个实数根,则α+β的值是( )A、3 B、1 C、﹣1 D、﹣312. 如图,在平面直角坐标系 中,B是反比例函数 的图象上的一点,则矩形OABC的面积为( )
A、1 B、2 C、3 D、411. 已知α、β是一元二次方程x2+x﹣2=0的两个实数根,则α+β的值是( )A、3 B、1 C、﹣1 D、﹣312. 如图,在平面直角坐标系 中,B是反比例函数 的图象上的一点,则矩形OABC的面积为( ) A、2 B、-2 C、1 D、413. 如图,在 中, ,且DE分别交AB,AC于点D,E,若 ,则△ 和△ 的面积之比等于( )
A、2 B、-2 C、1 D、413. 如图,在 中, ,且DE分别交AB,AC于点D,E,若 ,则△ 和△ 的面积之比等于( )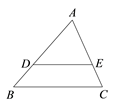 A、 B、 C、 D、14. 如图,抛物线 的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分函数图象如图所示,下列结论正确的有( )个.
A、 B、 C、 D、14. 如图,抛物线 的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分函数图象如图所示,下列结论正确的有( )个.
①abc>0; ②b2-4ac>0; ③3a+c=0;④方程 的两个根是x1=-1,x2=3;⑤当x<1时,y随x增大而减小.
A、2 B、3 C、4 D、5三、解答题
-
15.(1)、解方程 ;(2)、已知,关于x的一元二次方程 有两个实数根,求k的取值范围.16. 如图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.

⑴以点O为位似中心,在方格图中画出将△ABC放大为原来的2倍得到的△A′B′C′;
⑵△A′B′C′绕点B′顺时针旋转90°,画出旋转后得到的△A″B′C″,并求点A′旋转到点A″所经过的路线长(结果保留π).
17. 如图,在△ABC中,点D在AB边上,∠ABC=∠ACD,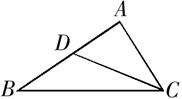 (1)、求证:△ABC∽△ACD(2)、若AD=2,AB=5.求AC的长.18. 组织一次排球邀请赛,参赛的每两个队都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,则比赛组织者应邀请多少个队参赛?19. 一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另外有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图所示).
(1)、求证:△ABC∽△ACD(2)、若AD=2,AB=5.求AC的长.18. 组织一次排球邀请赛,参赛的每两个队都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,则比赛组织者应邀请多少个队参赛?19. 一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另外有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图所示). (1)、从口袋中摸出一个小球,所摸球上的数字大于2的概率为 ;(2)、小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于5,那么小龙去;否则小东去.你认为游戏公平吗?请用树状图或列表法说明理由.20. 如图,反比例函数 与一次函数 的图象交于A(1,3)和B(-3,n)两点.
(1)、从口袋中摸出一个小球,所摸球上的数字大于2的概率为 ;(2)、小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于5,那么小龙去;否则小东去.你认为游戏公平吗?请用树状图或列表法说明理由.20. 如图,反比例函数 与一次函数 的图象交于A(1,3)和B(-3,n)两点. (1)、求m、n的值;(2)、当x取什么值时,一次函数的值大于反比例函数的值.(3)、求出△OAB的面积.21. 二次函数y=ax2﹣2ax﹣3(a≠0)的图象经过点A .
(1)、求m、n的值;(2)、当x取什么值时,一次函数的值大于反比例函数的值.(3)、求出△OAB的面积.21. 二次函数y=ax2﹣2ax﹣3(a≠0)的图象经过点A . (1)、求二次函数的对称轴;(2)、当A(﹣1,0)时,
(1)、求二次函数的对称轴;(2)、当A(﹣1,0)时,①求此时二次函数的表达式;
②把y=ax2﹣2ax﹣3化为y=a(x﹣h)2+k的形式,并写出顶点坐标;
③画出函数的图象.