云南省普洱市2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-10-13 类型:期末考试
一、填空题
-
1. 在一个不透明的袋子中有若干个小球,这些球除颜色外无其他差别,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,然后把它重新放回袋中并摇匀,不断重复上述过程.以下是利用计算机模拟的摸球试验统计表:
摸球实验次数
100
1000
5000
10000
50000
100000
“摸出黑球”的次数
36
387
2019
4009
19970
40008
“摸出黑球”的频率
(结果保留小数点后三位)
0.360
0.387
0.404
0.401
0.399
0.400
根据试验所得数据,估计“摸出黑球”的概率是(结果保留小数点后一位).
2. 若 ADE∽ ACB,且 ,DE=10,则BC= .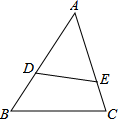 3. 中国“一带一路”给沿线国家和地区带来很大的经济效益,沿线某地区居民2016年人均年收入20000元,到2018年人均年收入达到39200元.则该地区居民年人均收入平均增长率为.(用百分数表示)4. 如图,在平面直角坐标系中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y= 的图象上,则k的值为.
3. 中国“一带一路”给沿线国家和地区带来很大的经济效益,沿线某地区居民2016年人均年收入20000元,到2018年人均年收入达到39200元.则该地区居民年人均收入平均增长率为.(用百分数表示)4. 如图,在平面直角坐标系中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y= 的图象上,则k的值为.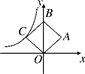 5. 若二次函数 的对称轴为直线 ,则关于 的方程 的解为 .6. 已知 分别切 于点 , 为 上不同于 的一点, ,则 的度数是 .
5. 若二次函数 的对称轴为直线 ,则关于 的方程 的解为 .6. 已知 分别切 于点 , 为 上不同于 的一点, ,则 的度数是 .二、单选题
-
7. 下列四个银行标志中,既是中心对称图形,又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 8. 下列事件为必然事件的是( )A、袋中有4个蓝球,2个绿球,共6个球,随机摸出一个球是红球 B、三角形的内角和为180° C、打开电视机,任选一个频道,屏幕上正在播放广告 D、抛掷一枚硬币两次,第一次正面向上,第二次反面向上9. 在某篮球邀请赛中,参赛的每两个队之间都要比赛一场,共比赛36场,设有x个队参赛,根据题意,可列方程为( )A、 B、 C、 D、10. 如图,二次函数 的图象经过点 , ,下列说法正确的是( )
8. 下列事件为必然事件的是( )A、袋中有4个蓝球,2个绿球,共6个球,随机摸出一个球是红球 B、三角形的内角和为180° C、打开电视机,任选一个频道,屏幕上正在播放广告 D、抛掷一枚硬币两次,第一次正面向上,第二次反面向上9. 在某篮球邀请赛中,参赛的每两个队之间都要比赛一场,共比赛36场,设有x个队参赛,根据题意,可列方程为( )A、 B、 C、 D、10. 如图,二次函数 的图象经过点 , ,下列说法正确的是( )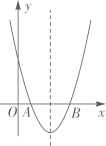 A、 B、 C、 D、图象的对称轴是直线11. 若关于x的一元二次方程 有两个实数根,则k的取值范围是( )A、 B、 C、 D、12. 如图, 是由等腰直角 经过位似变换得到的,位似中心在 轴的正半轴,已知 , 点坐标为 ,位似比为 ,则两个三角形的位似中心 点的坐标是( )
A、 B、 C、 D、图象的对称轴是直线11. 若关于x的一元二次方程 有两个实数根,则k的取值范围是( )A、 B、 C、 D、12. 如图, 是由等腰直角 经过位似变换得到的,位似中心在 轴的正半轴,已知 , 点坐标为 ,位似比为 ,则两个三角形的位似中心 点的坐标是( )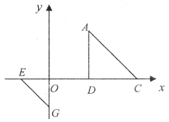 A、 B、 C、 D、13. 已知正比例函数 的图象与反比例函数 图象相交于点 ,下列说法正确的是( )A、反比例函数 的解析式是 B、两个函数图象的另一交点坐标为 C、当 或 时, D、正比例函数 与反比例函数 都随 的增大而增大14. 如图,在平面直角坐标系中,已知⊙D经过原点O , 与x轴、y轴分别交于A、B两点,B点坐标为(0,2 ),OC与⊙D相交于点C , ∠OCA=30°,则图中阴影部分的面积为( )
A、 B、 C、 D、13. 已知正比例函数 的图象与反比例函数 图象相交于点 ,下列说法正确的是( )A、反比例函数 的解析式是 B、两个函数图象的另一交点坐标为 C、当 或 时, D、正比例函数 与反比例函数 都随 的增大而增大14. 如图,在平面直角坐标系中,已知⊙D经过原点O , 与x轴、y轴分别交于A、B两点,B点坐标为(0,2 ),OC与⊙D相交于点C , ∠OCA=30°,则图中阴影部分的面积为( )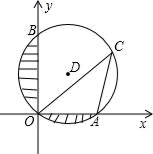 A、2π﹣2 B、4π﹣ C、4π﹣2 D、2π﹣
A、2π﹣2 B、4π﹣ C、4π﹣2 D、2π﹣三、解答题
-
15. 解方程:16. 码头工人每天往一艘轮船上装载货物,装载速度 (吨/天)与装完货物所需时间 (天)之间的函数关系如图.
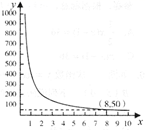 (1)、求 与 之间的函数表达式,并写出自变量 的取值范围;(2)、由于遇到紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸多少吨货物?17. 如图,在平面直角坐标系中,已知 的三个顶点的坐标分别为 , , .
(1)、求 与 之间的函数表达式,并写出自变量 的取值范围;(2)、由于遇到紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸多少吨货物?17. 如图,在平面直角坐标系中,已知 的三个顶点的坐标分别为 , , .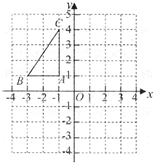 (1)、将 绕着点 顺时针旋转 后得到 ,请在图中画出 ;(2)、若把线段 旋转过程中所扫过的扇形图形围成一个圆锥的侧面,求该圆锥底面圆的半径(结果保留根号).18. 为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.(1)、八(1)班抽中歌曲《我和我的祖国》的概率是;(2)、试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.19. 如图,在 中, , 平分 交 于点 ,将 绕点 顺时针旋转到 的位置,点 在 上.
(1)、将 绕着点 顺时针旋转 后得到 ,请在图中画出 ;(2)、若把线段 旋转过程中所扫过的扇形图形围成一个圆锥的侧面,求该圆锥底面圆的半径(结果保留根号).18. 为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.(1)、八(1)班抽中歌曲《我和我的祖国》的概率是;(2)、试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.19. 如图,在 中, , 平分 交 于点 ,将 绕点 顺时针旋转到 的位置,点 在 上.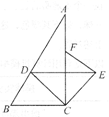 (1)、 旋转的度数为 ;(2)、连结 ,判断 与 的位置关系,并说明理由.20. 安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量 (千克)与每千克降价 (元) 之间满足一次函数关系,其图象如图所示:
(1)、 旋转的度数为 ;(2)、连结 ,判断 与 的位置关系,并说明理由.20. 安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量 (千克)与每千克降价 (元) 之间满足一次函数关系,其图象如图所示: (1)、求 与 之间的函数关系式;(2)、商贸公司要想获利2090元,则这种干果每千克应降价多少元?21. 如图,点D在以AB为直径的⊙O上,AD平分 , ,过点B作⊙O的切线交AD的延长线于点E .
(1)、求 与 之间的函数关系式;(2)、商贸公司要想获利2090元,则这种干果每千克应降价多少元?21. 如图,点D在以AB为直径的⊙O上,AD平分 , ,过点B作⊙O的切线交AD的延长线于点E .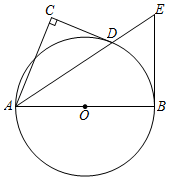 (1)、求证:直线CD是⊙O的切线.(2)、求证: .22. 数学活动课上,张老师引导同学进行如下探究:如图1,将长为 的铅笔 斜靠在垂直于水平桌面 的直尺 的边沿上,一端 固定在桌面上,图2是示意图.(1)、活动一
(1)、求证:直线CD是⊙O的切线.(2)、求证: .22. 数学活动课上,张老师引导同学进行如下探究:如图1,将长为 的铅笔 斜靠在垂直于水平桌面 的直尺 的边沿上,一端 固定在桌面上,图2是示意图.(1)、活动一如图3,将铅笔 绕端点 顺时针旋转, 与 交于点 ,当旋转至水平位置时,铅笔 的中点 与点 重合.
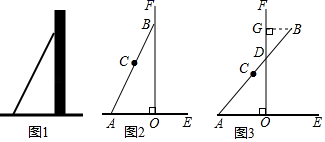
数学思考
设 ,点 到 的距离 .
①用含 的代数式表示: 的长是 , 的长是 ;
② 与 的函数关系式是 , 自变量 的取值范围是 .
(2)、活动二①列表:根据(1)中所求函数关系式计算并补全表格.
6
5
4
3.5
3
2.5
2
1
0.5
0
0
0.55
1.2
1.58
1.0
2.47
3
4.29
5.08
②描点:根据表中数值,描出①中剩余的两个点 .
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
数学思考
(3)、请你结合函数的图象,写出该函数的两条性质或结论.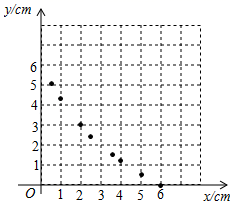 23. 如图,二次函数 的图象与 轴交于点 和点 ,与 轴交于点 ,以 为边在 轴上方作正方形 ,点 是 轴上一动点,连接 ,过点 作 的垂线与 轴交于点 .
23. 如图,二次函数 的图象与 轴交于点 和点 ,与 轴交于点 ,以 为边在 轴上方作正方形 ,点 是 轴上一动点,连接 ,过点 作 的垂线与 轴交于点 .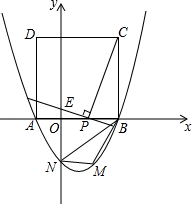 (1)、求该抛物线的函数关系表达式;(2)、当点 在线段 (点 不与 重合)上运动至何处时,线段 的长有最大值?并求出这个最大值;(3)、在第四象限的抛物线上任取一点 ,连接 .请问: 的面积是否存在最大值?若存在,求出此时点 的坐标;若不存在,请说明理由.
(1)、求该抛物线的函数关系表达式;(2)、当点 在线段 (点 不与 重合)上运动至何处时,线段 的长有最大值?并求出这个最大值;(3)、在第四象限的抛物线上任取一点 ,连接 .请问: 的面积是否存在最大值?若存在,求出此时点 的坐标;若不存在,请说明理由.