云南省昆明市盘龙区2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-10-13 类型：期末考试

进入出卷网下载

一、填空题

1. 若点P（3，﹣1）与点Q关于原点对称，则点Q的坐标是．

查看试题解析
2. 在一个不透明的盒子中装有 $a$ 个除颜色外完全相同的球，其中只有2个白球．若每次将球充分搅匀后，任意摸出1个球记下颜色后再放回盒子，通过大量重复实验后，发现摸到白球的频率稳定在20％左右，则 $a$ 的值约为．

查看试题解析
3. 如图，点A ， B ， C ， D在 $⊙ O$ 上， $\overset{⌢}{C B} = \overset{⌢}{C D}$ ， $∠ C A D = 30 °$ ， $∠ A C D = 50 °$ ，则 $∠ A C B =$ ．

查看试题解析
4. 如图，△DEF是△ABC经过位似变换得到的，点O是位似中心，已知OD：OA＝1：2，若△ABC的面积为5，则△DEF的面积为．

查看试题解析
5. 如图，在平面直角坐标系中，点 $B$ 在第一象限， $B A ⊥ x$ 轴于点 $A$ ，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象与线段 $A B$ 相交于点 $C$ ，且 $C$ 是线段 $A B$ 的中点，若 $Δ O A B$ 的面积为3，则 $k$ 的值为．

查看试题解析
6. 如图，抛物线y＝ax²＋bx＋c（a≠0）的对称轴为直线x＝1，与x轴的一个交点坐标为（﹣1，0），与y轴的交点坐标为（0，3）其部分图象如图所示，下列结论：
①2a＋b＝0；

②b²﹣4ac＜0；

③方程ax²＋bx＋c＝0的两个根是x₁＝﹣1，x₂＝2；

④将y＝ax²先向右平移1个单位，再向上平移4个单位可得到y＝ax²＋bx＋c的图象；

⑤当y＞0时，x的取值范围是﹣1＜x＜3

其中正确的结论是．（填序号）

查看试题解析

二、单选题

7. 我国民间，流传着许多含有吉祥意义的文字图案，表示对幸福生活的向往，良辰佳节的祝贺.比如下列图案分别表示“福”、“禄”、“寿”、“喜”，其中是中心对称图形的是（）

A、①③ B、①④ C、②③ D、②④

查看试题解析
8. 下列说法正确的是（）

A、任意掷一枚质地均匀的硬币10次，一定有5次正面向上 B、通过抛掷一枚均匀的硬币确定谁先发球的比赛规则是不公平的 C、“367 人中至少有2人生日相同”是必然事件 D、“垂直于弦的直径平分这条弦”是不确定事件

查看试题解析
9. 当温度不变时，气球内气体的气压P（单位：kPa）是气体体积V（单位：m³）的函数，下表记录了一组实验数据：P与V的函数关系式可能是（）
V（单位：m³）
1
1.5
2
2.5
3
P（单位：kPa）
96
64
48
38.4
32

A、P=96V B、P=﹣16V+112 C、P=16V²﹣96V+176 D、P= $\frac{96}{v}$

查看试题解析
10. Rt△ABC中，∠C=90°，AC=3，BC=4，把它沿AC所在直线旋转一周，则所得几何体的侧面积是（）

A、12π B、15π C、20π D、36π

查看试题解析
11. 如图，一农户要建一个矩形花圃，花圃的一边利用长为12m的住房墙，另外三边用25m长的篱笆围成，为方便进出，在垂直于住房墙的一边留一个1m宽的门，花圃面积为80m² ，设与墙垂直的一边长为xm（已标注在图中），则可以列出关于x的方程是（）

A、x（26﹣2x）＝80 B、x（24﹣2x）＝80 C、（x﹣1）（26﹣2x）＝80 D、x（25﹣2x）＝80

查看试题解析
12. 对于反比例函数y＝﹣ $\frac{3}{x}$ ，下列说法错误的是（）

A、它的图象在第二、四象限 B、在每个象限内y随x的增大而增大 C、若x＞1，则﹣3＜y＜0 D、若点A （﹣1，y₁）和点B （3，y₂）在这个函数图象上，则y₁＜y₂

查看试题解析
13. 如图，△ABC的内切圆⊙O与BC，CA，AB分别相切于点D，E，F，且AB＝5，BC＝13，CA＝12，则阴影部分(即四边形AEOF)的面积是（）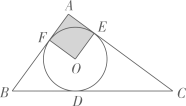

A、4 B、6.25 C、7.5 D、9

查看试题解析
14. 如图，某班数学兴趣小组利用数学知识测量建筑物DEFC的高度.他们从点A出发沿着坡度为i＝1：2.4的斜坡AB步行26米到达点B处，此时测得建筑物顶端C的仰角α＝35°，建筑物底端D的俯角β＝30°.若AD为水平的地面，则此建筑物的高度CD约为（）米.（参考数据： $\sqrt{3}$ ≈1.7，tan35°≈0.7）

A、23.1 B、21.9 C、27.5 D、30

查看试题解析

三、解答题

15. 计算：2sin30°＋cos45°﹣ ${(\frac{1}{4})}^{- 1}$ ＋（π﹣3.14）⁰

查看试题解析
16. 已知关于x的一元二次方程x²﹣4x＋m＝0

(1)、当m为何值时，方程有两个相等的实数根；

(2)、当m＝﹣12，求此一元二次方程的根．

查看试题解析
17. 如图，在边长为1的正方形网格中，△ABC的顶点均在格点上，点A、B的坐标分别是A（5，3）、B（5，1）．

(1)、①在图中标出△ABC外心D的位置，并直接写出它的坐标；
②将△ABC绕点C逆时针方向旋转90°后，得到△A′B′C ，画出旋转后的△A′B′C；

(2)、求△ABC旋转过程中点A经过的路径长．

查看试题解析
18. 复工复学后，为防控冠状病毒，学生进校园必须戴口罩，测体温.某校开通了两种不同类型的测温通道共三条.分别为：红外热成像测温( $A$ 通道)和人工测温( $B$ 通道和 $C$ 通道)．在三条通道中，每位同学都可随机选择其中的一条通过，周五有甲、乙两位同学进校园．

(1)、当甲同学进校园时，从人工测温通道通过的概率是．

(2)、请用列表或画树状图的方法求甲、乙两位同学从不同类型测温通道通过的概率．

查看试题解析
19. 如图，一次函数y=x+b和反比例函数y= $\frac{k}{x}$ （k≠0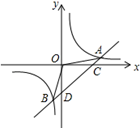）交于点A（4，1）．

(1)、求反比例函数和一次函数的解析式；

(2)、求△AOB的面积；

(3)、根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围．

查看试题解析
20. 如图，在正方形ABCD中，点E是AB的中点，延长BC到点F ，使CF＝AE ．

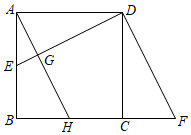(1)、求证：△ADE≌△CDF；

(2)、在（1）的条件下，把△ADE绕点D逆时针旋转°后与△CDF重合；

(3)、现把△DCF向左平移，使DC与AB重合，得△ABH ， AH交ED于点G ．若AB＝4，求EG的长．

查看试题解析
21. 某商场经销一种高档水果，原价每千克50元．

(1)、连续两次降价后每千克32元，若每次下降的百分率相同，求每次下降的百分率；

(2)、若每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，商场决定采取适当的涨价措施，但商场规定每千克涨价不能超过8元，若每千克涨价1元，日销售量将减少20千克，现该商场要保证每天获利最多，那么每千克应涨价多少元？

查看试题解析
22. 如图，以△ABC的边AB为直径的⊙O与边AC相交于点D ， BC是⊙O的切线，E为BC的中点，连接BD、DE ．

(1)、求证：DE是⊙O的切线；

(2)、设△CDE的面积为S₁ ，四边形ABED的面积为S₂ ，若S₂＝5S₁ ，求tan∠BAC的值．

查看试题解析
23. 如图，二次函数y= $\frac{4}{3}$ x²+bx+c的图象与x轴交于A（3，0），B（-1，0），与y轴交于点C ．若点P ， Q同时从A点出发，都以每秒1个单位长度的速度分别沿AB ， AC边运动，其中一点到达端点时，另一点也随之停止运动．

(1)、求该二次函数的解析式及点C的坐标；

(2)、当点P运动到B点时，点Q停止运动，这时，在x轴上是否存在点E ，使得以A ， E ， Q为顶点的三角形为等腰三角形？若存在，请求出E点坐标；若不存在，请说明理由．

(3)、当P ， Q运动到t秒时，△APQ沿PQ翻折，点A恰好落在抛物线上D点处，请判定此时四边形APDQ的形状，并求出D点坐标．

查看试题解析

V（单位：m³）	1	1.5	2	2.5	3
P（单位：kPa）	96	64	48	38.4	32