云南省建水县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-10-13 类型:期末考试
一、填空题
-
1. 已知点A(-3,2)与点B(a , b)关于原点对称,则a+b= .2. 抛物线 的顶点坐标为 .3. 某超市一月份的营业额为300万元,已知三月份的营业额为363万元,如果平均每月的增长率为x,由题意列方程.4. 袋子中装有除颜色外完全相同的n个黄色乒乓球和2个白色乒乓球,从中随机抽取1个,若选中白色乒乓球的概率是 ,则n的值是 .5. 一个扇形的半径为60cm,圆心角为120°,用它做一个圆锥的侧面,则圆锥的底面半径为 .6. 已知一列数:a , b , a+b , a+2b , 2a+3b , 3a+5b , …,按照这个规律写下去,第8个数是 .
二、单选题
-
7. 下列交通标志中,是轴对称图形但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
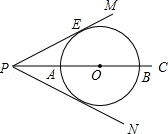
D、 8. 一次掷两枚质地均匀的硬币,出现两枚硬币都正面朝上的概率是( )A、 B、 C、 D、9. 若关于x的一元二次方程(a+1)x2+x+|a|-1=0的一个根是0,则实数a的值为( )A、a=1 B、a=-1 C、a=±1 D、a=010. 如图,在⊙O中, ,∠AOD=150°,∠BOC=80°,则∠AOB的度数是( )
8. 一次掷两枚质地均匀的硬币,出现两枚硬币都正面朝上的概率是( )A、 B、 C、 D、9. 若关于x的一元二次方程(a+1)x2+x+|a|-1=0的一个根是0,则实数a的值为( )A、a=1 B、a=-1 C、a=±1 D、a=010. 如图,在⊙O中, ,∠AOD=150°,∠BOC=80°,则∠AOB的度数是( ) A、20° B、25° C、30° D、35°11. 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是31,设每个支干长出x个小分支,则下列方程中正确的是( )A、1+x2=31 B、1+x+x2=31 C、x+x2=31 D、(1+x)2=3112. 二次函数y=a +bx+c(a≠0)的图象如图所示,那么一次函数y= x+c的图象可能是( )
A、20° B、25° C、30° D、35°11. 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是31,设每个支干长出x个小分支,则下列方程中正确的是( )A、1+x2=31 B、1+x+x2=31 C、x+x2=31 D、(1+x)2=3112. 二次函数y=a +bx+c(a≠0)的图象如图所示,那么一次函数y= x+c的图象可能是( )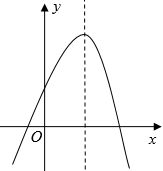 A、
A、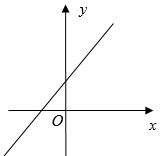 B、
B、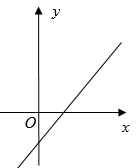 C、
C、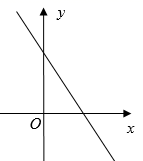 D、
D、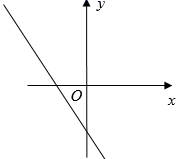 13. 如图,AB是⊙O的直径,弦CD⊥AB于点E , 若AB=20,AE=2,则弦CD的长是( )
13. 如图,AB是⊙O的直径,弦CD⊥AB于点E , 若AB=20,AE=2,则弦CD的长是( ) A、6 B、8 C、10 D、1214. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( )
A、6 B、8 C、10 D、1214. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( )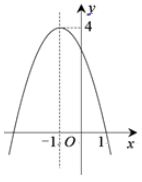 A、其图象关于直线x=-1对称 B、函数y=ax2+bx+c(a≠0)的最大值为4 C、1和-3是方程ax2+bx+c=0(a≠0)的两个根 D、当x<-1时,y随x的增大而减小
A、其图象关于直线x=-1对称 B、函数y=ax2+bx+c(a≠0)的最大值为4 C、1和-3是方程ax2+bx+c=0(a≠0)的两个根 D、当x<-1时,y随x的增大而减小三、解答题
-
15. 解方程: .16. 若关于x的一元二次方程mx2-4x+3=0有两个不相等的实数根.(1)、求m的取值范围;(2)、若m为正整数,求此时方程的根.17. 在平面直角坐标系中的位置如图,其中每个小正方形的边长为1个单位长度.
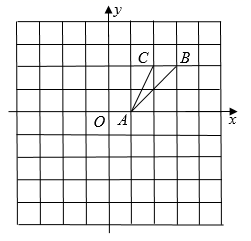 (1)、①画出 关于原点O对称的 ;
(1)、①画出 关于原点O对称的 ;②画出 绕点A逆时针方向旋转90°后的 ;
(2)、在②的条件下,求AC旋转扫过的面积(结果保留π).18. 如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2 , 两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为多少米. 19. 甲、乙玩转盘游戏时,把质地相同的两个转盘A、B平均分成2份和3份,并在每一份内标有数 字如图.游戏规则:甲、乙两人分别同时转动两个转盘各一次,当转盘停止后,指针所在区域的数字之和为偶数 时甲获胜;数字之和为奇数时乙获胜.若指针落在分界线上,则需要重新转动转盘.
19. 甲、乙玩转盘游戏时,把质地相同的两个转盘A、B平均分成2份和3份,并在每一份内标有数 字如图.游戏规则:甲、乙两人分别同时转动两个转盘各一次,当转盘停止后,指针所在区域的数字之和为偶数 时甲获胜;数字之和为奇数时乙获胜.若指针落在分界线上,则需要重新转动转盘.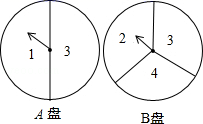 (1)、用画树状图或列表的方法,求甲获胜的概率;(2)、这个游戏对甲、乙双方公平吗?请判断并说明理由.20. 如图,⊙O的直径AB为6cm,∠ACB的平分线交⊙O于点D .
(1)、用画树状图或列表的方法,求甲获胜的概率;(2)、这个游戏对甲、乙双方公平吗?请判断并说明理由.20. 如图,⊙O的直径AB为6cm,∠ACB的平分线交⊙O于点D . (1)、判断 的形状,并证明;(2)、求BD的长.21. 某商场销售一批工艺品,平均每天可售出20件,每件赢利45元,为了扩大销售,增加利润,尽量减少库存,商场决定釆取适当的降价措施.经调查发现,如果每件工艺品每降价1元,商场平均每天可多售出4件.(1)、设每件工艺品降价x元,商场销售这种工艺品每天盈利y元,求出y与x之间的函数关系式;(2)、每件工艺品降价多少元时,才能使每天利润最大,最大利润为多少?
(1)、判断 的形状,并证明;(2)、求BD的长.21. 某商场销售一批工艺品,平均每天可售出20件,每件赢利45元,为了扩大销售,增加利润,尽量减少库存,商场决定釆取适当的降价措施.经调查发现,如果每件工艺品每降价1元,商场平均每天可多售出4件.(1)、设每件工艺品降价x元,商场销售这种工艺品每天盈利y元,求出y与x之间的函数关系式;(2)、每件工艺品降价多少元时,才能使每天利润最大,最大利润为多少?