云南省红河哈尼族彝族自治州河口瑶族自治县2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-10-13 类型：期末考试

进入出卷网下载

一、单选题

1. 下列汉字中既是轴对称，又是中心对称的是（）．

A、美 B、丽 C、河 D、口

查看试题解析
2. 下列事件中，是确定性事件的是（）．

A、随意翻到一本书的某页，这页的页码是奇数页； B、汽车累计行驶10000公里，从未出现故障； C、明天的太阳从东方升起； D、河口明天会下雨；

查看试题解析
3. 将抛物线 $y = \frac{1}{2} x^{2}$ ，向左平移1个单位，再向下平移2个单位后，所得的抛物线是（）．

A、 $y = \frac{1}{2} {(x + 1)}^{2} + 2$ B、 $y = \frac{1}{2} {(x - 1)}^{2} - 2$ C、 $y = \frac{1}{2} {(x + 1)}^{2} - 2$ D、 $y = \frac{1}{2} {(x - 1)}^{2} + 2$

查看试题解析
4. 若关于 $x$ 的一元二次方程 $k x^{2} - 2 x - 1 = 0$ 有两个不相等的实数根，则 $k$ 的取值范围是（）．

A、 $k > - 1$ 且 $k \neq 0$ B、 $k < - 1$ 且 $k \neq 0$ C、 $k < 1$ D、 $k > - 1$

查看试题解析
5. 如图， $P A$ 和 $P B$ 是 $⊙ O$ 的切线，点 $A$ 和点 $B$ 为切点， $A C$ 是 $⊙ O$ 的直径．已知 $∠ P = 60 °$ ，那么 $∠ A C B$ 的大小是（）．

A、65° B、60° C、55° D、50°

查看试题解析
6. 二次函数y＝ax²+bx+c（a≠0）的图象如图所示，那么下列说法正确的是（　　）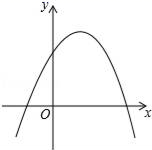

A、a＞0，b＞0，c＞0 B、a＜0，b＞0，c＞0 C、a＜0，b＞0，c＜0 D、a＜0，b＜0，c＞0

查看试题解析
7. 香蕉是河口县的主要农副产品之一，香蕉的种植备受当地各农户的青睐．香蕉种植中，要注意病毒预防，香蕉有一种病叫“香蕉黄叶病”（又称“香蕉巴拿马病”），是一种通过土壤传播的香蕉传染病，染病香蕉逐步枯萎死亡，且因为土壤遗留，发病地区30年以上不能种植香蕉，是香蕉的“不治之症”．如果某农户家的一块香蕉地中有一棵香蕉感染了“巴拿马病毒”，经过两轮传染后有81棵香蕉被传染．请你用学过的知识分析，每轮传染中平均每棵香蕉传染的棵数为（）．

A、8棵 B、9棵 C、10棵 D、11棵

查看试题解析

8. 小张承包了一片荒山，他想把这片荒山改造成一个橡胶园，现在有一种橡胶树树苗，它的成活率如下表所示，则下面推断中，其中合理的是（）．

移植棵数 $(n)$	成活数 $(m)$	成活率 $(m / n)$	移植棵数 $(n)$	成活数 $(m)$	成活率 $(m / n)$
50	47	$0.940$	1500	1335	$0.890$
270	235	$0.870$	3500	3203	$0.915$
400	369	0.923	7000	6335	$0.905$
750	662	$0.883$	14000	12628	$0.902$

下面有四个推断：

①小张移植3500棵这种树苗，成活率肯定高于 $0.890$ ；②随着移植棵数的增加，树苗成活的频率总在 $0.900$ 附近摆动，显示出一定的稳定性，可以估计树苗成活的概率是 $0.900$ ；③若小张移植10000棵这种树苗，则可能成活9000棵；④若小张移植20000棵这种树苗，则一定成活率18000棵．

A、①② B、①④ C、②③ D、②④

查看试题解析

二、填空题

9. 在平面直角坐标系 $x O y$ 中，点 $M (2 ， - 3)$ 与点 $N$ 关于原点 $O$ 中心对称，则点 $N$ 的坐标是．

查看试题解析
10. 二次函数 $y = - \frac{1}{3} {(x - 1)}^{2} + 3$ 的顶点坐标是．

查看试题解析
11. 已知关于 $x$ 的方程 $x^{2} + 6 x + m^{2} - 2 m + 5 = 0$ 的一个根是1，则 $2 m^{2} - 4 m =$ ．

查看试题解析
12. 如图， $A B$ 、 $C D$ 是 $⊙ O$ 的两条弦，连接 $A D$ 、 $B C$ ．若 $∠ B A D = 60 °$ ，则 $∠ B C D$ 的度数为度．

查看试题解析
13. 西气东输工程全长四千多千米，其中有成千上万个圆弧形弯管．制作弯管时，需要先按中心线计算“展直长度”再下料．如图，计算图中管道的全长（精确到 $1 c m$ ）．

查看试题解析
14. 如图，以等边△ABC的一边AB为直径的半圆O交AC于点D，交BC于点E，若AB=4，则阴影部分的面积是.

查看试题解析

三、解答题

15. 用适当的方法解下列方程．

(1)、 $x^{2} - 13 x + 36 = 0$

(2)、 ${(x - 3)}^{2} - 3 x (x - 3) = 0$

查看试题解析
16. 如图，已知 $△ A B C$ 三个顶点的坐标分别是 $A (0 ， 2)$ ， $B (3 ， 3)$ ， $C (2 ， 1)$ ．

⑴画出 $△ A B C$ 关于原点对称的 $△ A_{1} B_{1} C_{1}$ ，并直接写出 $C_{1}$ 的坐标；

⑵画出 $△ A B C$ 绕点 $A$ 顺时针方向旋转90°后得到的 $△ A_{2} B_{2} C_{2}$ ，并求出线段 $A B$ 扫过的面积．

查看试题解析
17. 河口瑶族自治县位于红河哈尼族彝族自治州东南部，隔红河与越南老街市、谷柳市相望，是云南唯一一个以瑶族为主体的自治县．瑶族人民的粽粑是当地一种美味的特色小吃，包粽粑是瑶族传统的“盘王节”（农历十月十六）活动之一．盘王节那天，小盘同学回家看到桌子上有一盘粽粑，其中花生仁、紫苏仁各1，豆沙仁2个，这些粽粑除陷外，其它无差别．

(1)、小盘随机地从盘子中取一个粽粑，求取出的是花生仁的概率；

(2)、小盘随机地从盘子中取出两个粽粑，请用列表法或画树状图法表示所有可能的结果，并求出小盘取出的两个粽粑都是豆沙粽粑的概率．

查看试题解析
18. 已知二次函数的图象以点 $A (- 1 ， 4)$ 为顶点，且过点 $B (2 ， - 5)$ ．

(1)、求该函数的解析式；

(2)、直接写出 $y$ 随 $x$ 的增大而增大时自变量 $x$ 的取值范围．

查看试题解析
19. 快手、抖音等各大娱乐APP软件深受人们的喜爱，但随着电商时代的热潮，曾经以直播、娱乐为主的主播也开始转型为带货主播．某快手主播，从今年九月份开始直播带货，并深受粉丝的喜爱，并从十月份该主播就开始盈利36000元，十二月的盈利达到43560元，且从十月到十二月，每月的盈利的平均增长率都相同．

(1)、求每月盈利的平均增长率；

(2)、按照这个平均增长率，预计下个月（即元月份）该主播的盈利将达到多少元？

查看试题解析
20. 如图，已知圆锥的底面半径 $r$ 为 $10 c m$ ，母线长为 $40 c m$ ．求它的侧面展开扇形的圆心角的度数和它的全面积．

查看试题解析
21. 如图，AB是⊙O的直径，AC是弦，OD⊥AC于点D，过点A作⊙O的切线AP，AP与OD的延长线交于点P，连接PC、BC．

(1)、猜想：线段OD与BC有何数量和位置关系，并证明你的结论．

(2)、求证：PC是⊙O的切线.

查看试题解析
22. 某大学生创业团队抓住商机，购进一批干果分装成营养搭配合理的小包装后出售，每袋成本3元.试销期间发现每天的销售量y（袋）与销售单价x（元）之间满足一次函数关系，部分数据如表所示，其中3.5≤x≤5.5，另外每天还需支付其他费用80元.

销售单价 $x$ （元）

3.5

5.5

销售量 $y$ （袋）

280

120

(1)、请直接写出y与x之间的函数关系式；

(2)、如果每天获得160元的利润，销售单价为多少元？

(3)、设每天的利润为w元，当销售单价定为多少元时，每天的利润最大？最大利润是多少元？

查看试题解析
23. 如图，抛物线 $y = x^{2} - 2 x - 3$ 与 $x$ 轴交于 $A$ 、 $B$ 两点．

(1)、抛物线与 $x$ 轴的交点坐标为；

(2)、求抛物线与坐标轴围成的 $△ A B C$ 的面积；

(3)、设（1）中的抛物线上有一个动点 $P$ ，当点 $P$ 在该抛物线上滑动到什么位置时，满足 $S_{△ P A B} = 6$ ，并求出此时 $P$ 点的坐标．

查看试题解析

销售单价 $x$ （元）	3.5	5.5
销售量 $y$ （袋）	280	120