山西省运城市盐湖区2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-10-13 类型:期末考试
一、单选题
-
1. 一元二次方程 的根为( )A、 B、 C、 D、2. 图中的三视图所对应的几何体是( )
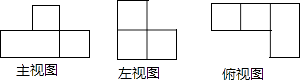 A、
A、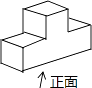 B、
B、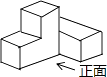 C、
C、 D、
D、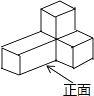 3. 点 在反比例函数 的图象上,则下列各点在此函数图象上的是( )A、 B、 C、 D、4. 如图,两条直线分别被三条平行直线l1 , l2 , l3所截,若AB=3,BC=6,DE=2,则DF的长为( )
3. 点 在反比例函数 的图象上,则下列各点在此函数图象上的是( )A、 B、 C、 D、4. 如图,两条直线分别被三条平行直线l1 , l2 , l3所截,若AB=3,BC=6,DE=2,则DF的长为( ) A、4 B、5 C、6 D、75. 某鱼塘里养了1600条鲤鱼,若干条草鱼和800条鲢鱼,该鱼塘主通过多次捕捞试验后发现,捕捞到草鱼的频率稳定在0.5左右,则该鱼塘捞到鲢鱼的概率约为( )A、 B、 C、 D、6. 如图所示, 在正方形网格中的位置如图所示( 均在格点上), 于点 .下列四个选项中正确的是( )
A、4 B、5 C、6 D、75. 某鱼塘里养了1600条鲤鱼,若干条草鱼和800条鲢鱼,该鱼塘主通过多次捕捞试验后发现,捕捞到草鱼的频率稳定在0.5左右,则该鱼塘捞到鲢鱼的概率约为( )A、 B、 C、 D、6. 如图所示, 在正方形网格中的位置如图所示( 均在格点上), 于点 .下列四个选项中正确的是( ) A、 B、 C、 D、7. 2020年12月17日凌晨,探月工程嫦娥五号返回器在内蒙古四子王旗预定区域成功着陆,标志着中国首次月球采样返回任务圆满成功!为庆祝这一历史性事件,某社区准备制作一幅宣传版面,喷绘时为了美观,要在矩形图案四周外围增加一圈等宽的白边,已知图案的长为2米,宽为1米,图案面积占整幅宣传版面面积的 ,若设白边的宽为x米,则根据题意可列出方程( )A、 B、 C、 D、8. 如图,平面直角坐标系中,已知 顶点 ,以原点 为位似中心,将 缩小后得到 ,若 的面积为 ,则 的面积为( )
A、 B、 C、 D、7. 2020年12月17日凌晨,探月工程嫦娥五号返回器在内蒙古四子王旗预定区域成功着陆,标志着中国首次月球采样返回任务圆满成功!为庆祝这一历史性事件,某社区准备制作一幅宣传版面,喷绘时为了美观,要在矩形图案四周外围增加一圈等宽的白边,已知图案的长为2米,宽为1米,图案面积占整幅宣传版面面积的 ,若设白边的宽为x米,则根据题意可列出方程( )A、 B、 C、 D、8. 如图,平面直角坐标系中,已知 顶点 ,以原点 为位似中心,将 缩小后得到 ,若 的面积为 ,则 的面积为( ) A、 B、 C、 D、9. 如图,菱形 对角线 , 交于点 , ,过点 作 交 的延长线于点 .若菱形 的面积为4,则菱形的边长为( )
A、 B、 C、 D、9. 如图,菱形 对角线 , 交于点 , ,过点 作 交 的延长线于点 .若菱形 的面积为4,则菱形的边长为( ) A、 B、2 C、 D、410. 某广场有一个小型喷泉,水流从垂直于地面的水管 喷出, 长为 .水流在各个方向上沿形状相同的抛物线路径落到地面上,某方向上抛物线路径的形状如图所示,落点B到O的距离为 .建立平面直角坐标系,水流喷出的高度 与水平距离 之间近似满足函数关系 ,则水流喷出的最大高度为( )
A、 B、2 C、 D、410. 某广场有一个小型喷泉,水流从垂直于地面的水管 喷出, 长为 .水流在各个方向上沿形状相同的抛物线路径落到地面上,某方向上抛物线路径的形状如图所示,落点B到O的距离为 .建立平面直角坐标系,水流喷出的高度 与水平距离 之间近似满足函数关系 ,则水流喷出的最大高度为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知 ,则 的值为 .12. 将抛物线 向右平移2个单位,再向下平移1个单位,得到抛物线的解析式为 .13. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”.如图,P为 的黄金分割点( ),如果 的长度为 ,那么 的长度是 .(结果精确到 )
 14. 如图,在平面直角坐标系中,ABCO为平行四边形,O(0,0),A(3,1),B(1,2),反比例函数 的图象经过
14. 如图,在平面直角坐标系中,ABCO为平行四边形,O(0,0),A(3,1),B(1,2),反比例函数 的图象经过 OABC的顶点C,则k= .
OABC的顶点C,则k= .  15. 如图,矩形纸片 ,点E在边 上,连接 ,点F在线段 上,且 ,折叠矩形纸片使点C恰好落在点F处,折痕为 ,若 ,则折痕 的长为 .
15. 如图,矩形纸片 ,点E在边 上,连接 ,点F在线段 上,且 ,折叠矩形纸片使点C恰好落在点F处,折痕为 ,若 ,则折痕 的长为 .
三、解答题
-
16.(1)、计算:(2)、小亮在进行解一元二次方程的练习时,遇到这样一个方程: ,下面是他的解法:
第1步
第2步
第3步
填空:小亮是在第步开始出现错误的,这一步错误的原因是: .
(3)、请给出该方程正确的求解过程.17. 如图,是两棵树分别在同一时刻、同一路灯下的影子. (1)、①请画出路灯灯泡的位置(用字母 表示)
(1)、①请画出路灯灯泡的位置(用字母 表示)②在图中画出路灯灯杆(用线段 表示);
(2)、若左边树 的高度是4米,影长是3米,树根 离灯杆底的距离是1米,求灯杆的高度.18. 如图,在平面直角坐标系中,一次函数 的图象分别交x轴、y轴于A、B两点,与反比例函数 的图象交于C、D两点,已知点C的坐标是 , . (1)、求一次函数与反比例函数的表达式.(2)、求 的值.(3)、根据图象直接写出:当x为何值时,一次函数的值小于反比例函数的值?19. 阅读材料,回答下列问题:
(1)、求一次函数与反比例函数的表达式.(2)、求 的值.(3)、根据图象直接写出:当x为何值时,一次函数的值小于反比例函数的值?19. 阅读材料,回答下列问题:阿尔·花拉子米(约780 约850),著名阿拉伯数学家、天文学家、地理学家,是代数与算术的整理者,被誉为“代数之父”.他利用正方形图形巧妙解出了一元二次方程 的一个解.
将边长为x的正方形和边长为1的正方形,外加两个长方形,长为x , 宽为1,拼合在一起面积就是 ,即 ,而由原方程 变形得 ,即边长为 的正方形面积为36.所以 ,则 .
 (1)、上述求解过程中所用的方法与下列哪种方法是一致的__________.A、直接开平方法 B、公式法 C、配方法 D、因式分解法(2)、所用的数学思想方法是_______.A、分类讨论思想 B、数形结合思想 C、转化思想(3)、山西特产专卖店销售的某品牌枣夹核桃,进价为每袋20元,现在按每袋30元出售时,平均每天售出200袋,由于货源紧缺,现要涨价销售,经过市场调查发现,单价每上涨1元,则平均每天的销售会减少10袋,若该专卖店销售这种枣夹核桃每天的利润为y元,售价为x元,请求出y与x的函数解析式,再利用(1)的方法求出x是多少时,y最大,最大是多少?20. 共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标,共享出行、共享服务、共享物品、共享知识,制成编号为A、B、C、D的四张卡片(除字母和内容外,其余完全相同).现将这四张卡片背面朝上,洗匀放好.
(1)、上述求解过程中所用的方法与下列哪种方法是一致的__________.A、直接开平方法 B、公式法 C、配方法 D、因式分解法(2)、所用的数学思想方法是_______.A、分类讨论思想 B、数形结合思想 C、转化思想(3)、山西特产专卖店销售的某品牌枣夹核桃,进价为每袋20元,现在按每袋30元出售时,平均每天售出200袋,由于货源紧缺,现要涨价销售,经过市场调查发现,单价每上涨1元,则平均每天的销售会减少10袋,若该专卖店销售这种枣夹核桃每天的利润为y元,售价为x元,请求出y与x的函数解析式,再利用(1)的方法求出x是多少时,y最大,最大是多少?20. 共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标,共享出行、共享服务、共享物品、共享知识,制成编号为A、B、C、D的四张卡片(除字母和内容外,其余完全相同).现将这四张卡片背面朝上,洗匀放好. (1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)21. 为进一步加强疫情防控工作,避免在测温过程中出现人员聚集现象,某学校决定安装红外线体温监测仪,该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温,无需人员停留和接触,安装说明书的部分内容如表.
(1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)21. 为进一步加强疫情防控工作,避免在测温过程中出现人员聚集现象,某学校决定安装红外线体温监测仪,该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温,无需人员停留和接触,安装说明书的部分内容如表.名称
红外线体温检测仪
安装示意图

技术参数
探测最大角:∠OBC=73.14°
探测最小角:∠OAC=30.97°
安装要求
本设备需安装在垂直于水平地面AC的支架CP上
根据以上内容,解决问题:
学校要求测温区域的宽度AB为4m , 请你帮助学校确定该设备的安装高度OC .
(结果精确到0.1m , 参考数据:sin73.14°≈0.957,cos73.14°≈0.290,tan73.14°≈3.300,sin30.97°≈0.515,cos30.97°≈0.857,tan30.97°≈0.600)
22. 综合与实践在Rt△ABC中,∠ACB=90°,点D为斜边AB上的动点(不与点A , B重合).
 (1)、操作发现:如图①,当AC=BC=8时,把线段CD绕点C逆时针旋转90°得到线段CE , 连接DE , BE .
(1)、操作发现:如图①,当AC=BC=8时,把线段CD绕点C逆时针旋转90°得到线段CE , 连接DE , BE .①∠CBE的度数为;
②当BE=时,四边形CDBE为正方形;
(2)、探究证明:如图②,当BC=2AC时,把线段CD绕点C逆时针旋转90°后并延长为原来的两倍,记为线段CE , 连接DE , BE .①在点D的运动过程中,请判断∠CBE与∠A的大小关系,并证明;
②当CD⊥AB时,求证:四边形CDBE为矩形.
23. 如图,已知抛物线y=ax2+bx+3(a≠0)经过点A(1,0)和点B(3,0),与y轴交于点C.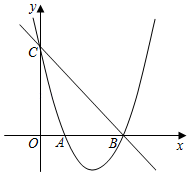 (1)、求此抛物线的解析式;(2)、若点P是直线BC下方的抛物线上一动点(不点B,C重合),过点P作y轴的平行线交直线BC于点D,设点P的横坐标为m.
(1)、求此抛物线的解析式;(2)、若点P是直线BC下方的抛物线上一动点(不点B,C重合),过点P作y轴的平行线交直线BC于点D,设点P的横坐标为m.①用含m的代数式表示线段PD的长.
②连接PB,PC,求△PBC的面积最大时点P的坐标.
(3)、设抛物线的对称轴与BC交于点E,点M是抛物线的对称轴上一点,N为y轴上一点,是否存在这样的点M和点N,使得以点C、E、M、N为顶点的四边形是菱形?如果存在,请直接写出点M的坐标;如果不存在,请说明理由.