山西省吕梁市兴县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-10-13 类型:期末考试
一、单选题
-
1. 民族图案是数学文化中的一块瑰宝.下列图案中,既不是中心对称图形也不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
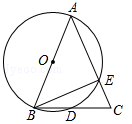
D、 2. 方程 的根的情况是( )A、有两个相等实数根 B、有两个不相等实数根 C、有一个实数根 D、无实数根3. 下列事件中是不可能事件的是( )A、守株待兔 B、瓮中捉鳖 C、水中捞月 D、百步穿杨4. 已知两圆的半径分别是一元二次方程x2-7x+12=0的两根,若这两个圆的圆心距为5,则这两圆的位置关系是( )A、相离 B、外切 C、相交 D、内切5. 如图,A、B、C、D四点都在⊙O上,若OC⊥AB,∠AOC=70°,则圆周角∠D的度数等于( )
2. 方程 的根的情况是( )A、有两个相等实数根 B、有两个不相等实数根 C、有一个实数根 D、无实数根3. 下列事件中是不可能事件的是( )A、守株待兔 B、瓮中捉鳖 C、水中捞月 D、百步穿杨4. 已知两圆的半径分别是一元二次方程x2-7x+12=0的两根,若这两个圆的圆心距为5,则这两圆的位置关系是( )A、相离 B、外切 C、相交 D、内切5. 如图,A、B、C、D四点都在⊙O上,若OC⊥AB,∠AOC=70°,则圆周角∠D的度数等于( ) A、70° B、50° C、35° D、20°6. 关于反比例函数y= ,下列说法错误的是( )A、图象关于原点成中心对称 B、当x>0时,y随x的增大而减小 C、图象与坐标轴无交点 D、图象位于第二、四象限7. 如图,扇形 中, ,以 为直径作半圆,若 ,则阴影部分的周长为( )
A、70° B、50° C、35° D、20°6. 关于反比例函数y= ,下列说法错误的是( )A、图象关于原点成中心对称 B、当x>0时,y随x的增大而减小 C、图象与坐标轴无交点 D、图象位于第二、四象限7. 如图,扇形 中, ,以 为直径作半圆,若 ,则阴影部分的周长为( )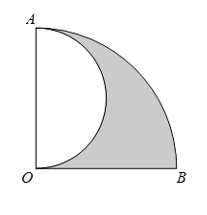 A、 B、 C、 D、8. 过原点的直线 与反比例函数 的图象交于点 ,则 的值为( )A、-2 B、-3 C、-5 D、-69. 某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为 的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度 随时间 (小时)变化的函数图象,其中 段是双曲线 的一部分,则当 时,大棚内的温度约为( )
A、 B、 C、 D、8. 过原点的直线 与反比例函数 的图象交于点 ,则 的值为( )A、-2 B、-3 C、-5 D、-69. 某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为 的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度 随时间 (小时)变化的函数图象,其中 段是双曲线 的一部分,则当 时,大棚内的温度约为( ) A、 B、 C、 D、10. 某商品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查反映;如调整价格,每涨价1元,每星期要少卖出10件.则每星期售出商品的利润y(单位:元)与每件涨价x(单位:元)之间的函数关系式是( )A、 B、 C、 D、
A、 B、 C、 D、10. 某商品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查反映;如调整价格,每涨价1元,每星期要少卖出10件.则每星期售出商品的利润y(单位:元)与每件涨价x(单位:元)之间的函数关系式是( )A、 B、 C、 D、二、解答题
-
11. 如图,若将△ABC绕点O顺时针旋转180°后得到△A′B′C′,则A点的对应点A′点的坐标是 .
 12. 选用适当的方法,解下列方程:(1)、(2)、(2x+3) 2=4 (2x+3) .13. 如图,AB是⊙O的直径,点C、D均在⊙O上,∠ACD=30°,弦AD=4cm .
12. 选用适当的方法,解下列方程:(1)、(2)、(2x+3) 2=4 (2x+3) .13. 如图,AB是⊙O的直径,点C、D均在⊙O上,∠ACD=30°,弦AD=4cm . (1)、求⊙O的直径.(2)、求 的长.14. 收音机刻度盘上的波长 和频率/的单位分别是米(m)和千赫兹(kM),
(1)、求⊙O的直径.(2)、求 的长.14. 收音机刻度盘上的波长 和频率/的单位分别是米(m)和千赫兹(kM),下面是波长 和频率 的一些对应值:
波长(m)
300
500
600
1000
1500
频率(kHz)
1000
600
500
300
200
(1)、根据表中数据特征可判断频率 是波长 的函数(填“正比例”或“反比例”或“一次”),其表达式为(2)、当频率 不超过 400kHz时,求波长 (米)的取值范围.15. 某住宅小区在住宅建设时留下一块1248平方米的空地,准备建一个矩形的露天游泳池,设计如图所示,游泳池的长是宽的2倍,在游泳池的前侧留一块5米宽的空地,其它三侧各保留2米宽的道路及1米宽的绿化带.请你计算出游泳池的长和宽. 16. 有一个可自由转动的转盘,被分成了4个相同的扇形,分别标有数1,2,3,4(如图所示),另有一个不透明的口袋装有分别标有数0,1,3的三个小球(除数字不同外,其余都相同),小亮转动一次转盘,停止后指针指向某一扇形(指针指向两个扇形的交线时,当作指向右边的扇形),扇形内的数是小亮的幸运数,小红任意摸出一个小球,小球上的数是小红的吉祥数,然后计算这两个数的积.
16. 有一个可自由转动的转盘,被分成了4个相同的扇形,分别标有数1,2,3,4(如图所示),另有一个不透明的口袋装有分别标有数0,1,3的三个小球(除数字不同外,其余都相同),小亮转动一次转盘,停止后指针指向某一扇形(指针指向两个扇形的交线时,当作指向右边的扇形),扇形内的数是小亮的幸运数,小红任意摸出一个小球,小球上的数是小红的吉祥数,然后计算这两个数的积. (1)、请你用画树状图或列表的方法,求这两个数的积为0的概率;(2)、小亮与小红做游戏,规则是:若这两个数的积为奇数,小亮赢;否则,小红赢.你认为该游戏公平吗?为什么?如果不公平,请你修改该游戏规则,使游戏公平.17. 如图①,AB是⊙O的直径,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D.
(1)、请你用画树状图或列表的方法,求这两个数的积为0的概率;(2)、小亮与小红做游戏,规则是:若这两个数的积为奇数,小亮赢;否则,小红赢.你认为该游戏公平吗?为什么?如果不公平,请你修改该游戏规则,使游戏公平.17. 如图①,AB是⊙O的直径,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D.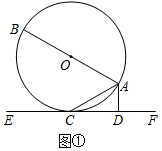
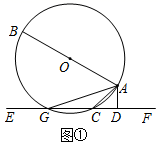 (1)、求证:∠DAC=∠BAC;(2)、若把直线EF向上平行移动,如图②,EF交⊙O于G、C两点,若题中的其它条件不变,猜想:此时与∠DAC相等的角是哪一个?并证明你的结论.18. 如图所示,一次函数 的图象与反比例函数 的图象交于 .
(1)、求证:∠DAC=∠BAC;(2)、若把直线EF向上平行移动,如图②,EF交⊙O于G、C两点,若题中的其它条件不变,猜想:此时与∠DAC相等的角是哪一个?并证明你的结论.18. 如图所示,一次函数 的图象与反比例函数 的图象交于 .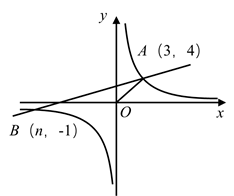 (1)、求反比例函数和一次函数的解析式;(2)、在x轴上存在一点C,使 为等腰三角形,求此时点C的坐标;(3)、根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围.19. 综合与实践
(1)、求反比例函数和一次函数的解析式;(2)、在x轴上存在一点C,使 为等腰三角形,求此时点C的坐标;(3)、根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围.19. 综合与实践某农作物的生长率p与温度r(℃)有如下关系∶如图,当10≤t≤25时可近似用函数P= t- 刻画∶当25≤t≤37时可近似用函数p=- (t-h)2+0.4刻画.
 (1)、求点h的值,(2)、按照经验,该作物提前上市的天数m(天)与生长率p之间满足已学过的函数关系,
(1)、求点h的值,(2)、按照经验,该作物提前上市的天数m(天)与生长率p之间满足已学过的函数关系,部分数据如下;
生长率p
0.2
0.25
0.3
0.35
提前上市的天数m (天)
0
5
10
15
求:①m关于p的函数表达式;
②用含t的代数式表示m;
③天气寒冷,大棚加温可改变农作物生长速度.大棚恒温 20℃时每天的成本为 100元,计划该作物 30天后上市,现根据市场调查;每提前一天上市售出(一次售完),销售额可增加 600 元.因此决定给大棚继续加温,但加温导致成本增加,估测加温到20≤t≤25 时的成本为200元/天,但若欲加温到25<t≤37,由于要采用特殊方法,成本增加到 400 元/天.问加温到多少度时增加的利润最大?并说明理由.(注∶ 农作物上市售出后大棚暂停使用)
三、填空题