山西省吕梁市交城县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-10-13 类型:期末考试
一、单选题
-
1. 一元二次方程 有实数根,则k的取值范围是( )A、 且 B、 C、 且 D、 或2. 二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x , y)对应值如表所示,则该函数图象的对称轴是( )
x
…
﹣3
﹣2
﹣1
0
1
…
y
…
﹣3
﹣2
﹣3
﹣6
﹣11
…
A、直线x=﹣3 B、y轴 C、直线x=﹣1 D、直线x=﹣23. 在以下”绿色食品、响应环保、可回收物、节水“四个标志图案中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 如图, 是 的直径, 是 的弦, ,下列说法错误的是( )
4. 如图, 是 的直径, 是 的弦, ,下列说法错误的是( ) A、 B、 C、 D、5. 有一首《对子歌》中唱到:天对地,雨对风,大陆对长空.现将“天,雨,大,空”四个字书写在材质、大小完全相同的卡片上,在暗箱搅匀后,随机抽取两张,恰为“天”、“空”二字的概率为( )A、 B、 C、 D、6. 如图,函数 (x>0)和 (x>0)的图象将第一象限分成三个区域,点M是②区域内一点,MN⊥x轴于点N,则△MON的面积可能是( )
A、 B、 C、 D、5. 有一首《对子歌》中唱到:天对地,雨对风,大陆对长空.现将“天,雨,大,空”四个字书写在材质、大小完全相同的卡片上,在暗箱搅匀后,随机抽取两张,恰为“天”、“空”二字的概率为( )A、 B、 C、 D、6. 如图,函数 (x>0)和 (x>0)的图象将第一象限分成三个区域,点M是②区域内一点,MN⊥x轴于点N,则△MON的面积可能是( )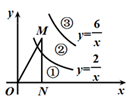 A、0.5. B、1. C、2. D、3.5.7. 大自然巧夺天工,一片小心树叶也蕴含着“黄金分割”.如图,P为AB的黄金分割点(AP >PB),如果AP的长度为8cm,那么AB的长度是( )
A、0.5. B、1. C、2. D、3.5.7. 大自然巧夺天工,一片小心树叶也蕴含着“黄金分割”.如图,P为AB的黄金分割点(AP >PB),如果AP的长度为8cm,那么AB的长度是( ) A、 -4 B、12- C、12+ D、 +48. 如图,在平行四边形ABCD中,E是AB的中点,F是AD的中点,FE交AC于O点,交CB的延长线于G点,那么S△AOF:S△COG=( )
A、 -4 B、12- C、12+ D、 +48. 如图,在平行四边形ABCD中,E是AB的中点,F是AD的中点,FE交AC于O点,交CB的延长线于G点,那么S△AOF:S△COG=( ) A、1:4 B、1:9 C、1:16 D、1:259. 如图, 的顶点O在坐标原点上, 边在x轴上, , ,把 绕点A按顺时针方向转到 ,使得点 的坐标是 则在这次旋转过程中线段 扫过部分(阴影部分)的面积为( )
A、1:4 B、1:9 C、1:16 D、1:259. 如图, 的顶点O在坐标原点上, 边在x轴上, , ,把 绕点A按顺时针方向转到 ,使得点 的坐标是 则在这次旋转过程中线段 扫过部分(阴影部分)的面积为( )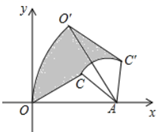 A、 B、 C、 D、10. 如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形O ,依此方式,绕点O连续旋转2021次得到正方形O ,如果点A的坐标为(1,0),那么点 的坐标为( )
A、 B、 C、 D、10. 如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形O ,依此方式,绕点O连续旋转2021次得到正方形O ,如果点A的坐标为(1,0),那么点 的坐标为( )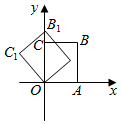 A、(1,1) B、(0, ) C、(0,﹣ ) D、(﹣1,1)
A、(1,1) B、(0, ) C、(0,﹣ ) D、(﹣1,1)二、填空题
-
11. 如图,在宽为18米、长为24米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为整个矩形面积的 ,设道路的宽为x米,则可列方程为 .
 12. 如图,直线y=kx+b与双曲线y= 相交于A(﹣2, ),B(1,﹣3)两点,则不等式kx+b< 的解集为 .
12. 如图,直线y=kx+b与双曲线y= 相交于A(﹣2, ),B(1,﹣3)两点,则不等式kx+b< 的解集为 .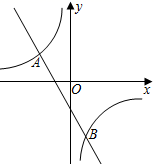 13. 以 为中心点的量角器与直角三角板 如图所示摆放,直角顶点 在零刻度线所在直线 上,且量角器与三角板只有一个公共点 ,若点 的读数为135°,则 的度数是 .
13. 以 为中心点的量角器与直角三角板 如图所示摆放,直角顶点 在零刻度线所在直线 上,且量角器与三角板只有一个公共点 ,若点 的读数为135°,则 的度数是 . 14. 如图,菱形 的边 轴,垂足为点 ,顶点 在第二象限,顶点 在 轴的正半轴上,反比例函数 的图象同时经过顶点 、 ,若点 的横坐标为1, .则 的值为 .
14. 如图,菱形 的边 轴,垂足为点 ,顶点 在第二象限,顶点 在 轴的正半轴上,反比例函数 的图象同时经过顶点 、 ,若点 的横坐标为1, .则 的值为 . 15. 如图,在Rt△ABC中,∠C=90°,AC=5cm , BC=3cm , 点P从点A出发,沿AB方向以每秒 cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1个单位长度的速度向终点C运动.设点P运动的时间为t秒,当△PBQ是直角三角形时,t的值为 .
15. 如图,在Rt△ABC中,∠C=90°,AC=5cm , BC=3cm , 点P从点A出发,沿AB方向以每秒 cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1个单位长度的速度向终点C运动.设点P运动的时间为t秒,当△PBQ是直角三角形时,t的值为 . 16. 小红家的阳台上放置了一个晒衣架,如图1,图2是晒衣架的侧面示意图,立杆AB、CD相交于点O,B、D两点在地面上,经测量得到AB=CD=136cm,OA=OC=51cm,OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32cm,垂挂在衣架上的连衣裙总长度小于多少时,连衣裙才不会拖在地面上?
16. 小红家的阳台上放置了一个晒衣架,如图1,图2是晒衣架的侧面示意图,立杆AB、CD相交于点O,B、D两点在地面上,经测量得到AB=CD=136cm,OA=OC=51cm,OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32cm,垂挂在衣架上的连衣裙总长度小于多少时,连衣裙才不会拖在地面上?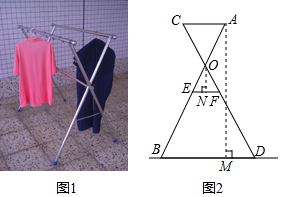
三、解答题
-
17.(1)、2x2+5x﹣1=0(用配方法解方程).(2)、6﹣2y=(y﹣3)2(用适当的方法解方程).18. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.
 (1)、点A的坐标为 , 点B的坐标为 , 点C的坐标为 .(2)、以原点O为位似中心,将△ABC放大,使变换后得到的△A1B1C1与△ABC对应边的比为2:1,请在网格内画出△A1B1C1 .(3)、求出△A1B1C1的面积.19. 共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标,共享出行、共享服务、共享物品、共享知识,制成编号为A、B、C、D的四张卡片(除字母和内容外,其余完全相同).现将这四张卡片背面朝上,洗匀放好.
(1)、点A的坐标为 , 点B的坐标为 , 点C的坐标为 .(2)、以原点O为位似中心,将△ABC放大,使变换后得到的△A1B1C1与△ABC对应边的比为2:1,请在网格内画出△A1B1C1 .(3)、求出△A1B1C1的面积.19. 共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标,共享出行、共享服务、共享物品、共享知识,制成编号为A、B、C、D的四张卡片(除字母和内容外,其余完全相同).现将这四张卡片背面朝上,洗匀放好. (1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)20. 第十五届中国上海国际艺术节期间,瑞士日内瓦大歌剧院芭蕾舞团芭蕾舞剧《吉赛尔》在市内的城市剧院演出,主办方工作人员准备利用一边靠墙(墙26米)的空旷场地为提前到场的观众设立面积为300平方米的封闭型长方形等候区.如图,为了方便观众进出,在两边空出两个宽各为1米的出入口,共用去隔栏绳48米.请问,工作人员围成的这个长方形的相邻两边长分别是多少米?
(1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)20. 第十五届中国上海国际艺术节期间,瑞士日内瓦大歌剧院芭蕾舞团芭蕾舞剧《吉赛尔》在市内的城市剧院演出,主办方工作人员准备利用一边靠墙(墙26米)的空旷场地为提前到场的观众设立面积为300平方米的封闭型长方形等候区.如图,为了方便观众进出,在两边空出两个宽各为1米的出入口,共用去隔栏绳48米.请问,工作人员围成的这个长方形的相邻两边长分别是多少米? 21. 如图,在平面直角坐标系xOy中,函数y=﹣x+5的图象与函数y= (x<0)的图象相交于点A , 并与x轴交于点C , S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
21. 如图,在平面直角坐标系xOy中,函数y=﹣x+5的图象与函数y= (x<0)的图象相交于点A , 并与x轴交于点C , S△AOC=15.点D是线段AC上一点,CD:AC=2:3. (1)、求k的值;(2)、直接写出不等式 >﹣x+5(x<0)的解集;(3)、若将△ODC绕点O逆时针旋转,得到△OD′C′,其中D′落在x轴负半轴上,判断点C′是否落在函数y= (x<0)的图象上,并说明理由.22. 如图,在 中, ,以AC为直径的⊙O与BC交于点D, ,垂足为E,ED的延长线与AC的延长线交于点F.
(1)、求k的值;(2)、直接写出不等式 >﹣x+5(x<0)的解集;(3)、若将△ODC绕点O逆时针旋转,得到△OD′C′,其中D′落在x轴负半轴上,判断点C′是否落在函数y= (x<0)的图象上,并说明理由.22. 如图,在 中, ,以AC为直径的⊙O与BC交于点D, ,垂足为E,ED的延长线与AC的延长线交于点F. (1)、求证:DE是⊙O的切线;(2)、若⊙O的半径为2, ,求CF的长.23. 如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c经过A(﹣3,0)、B(1,0)两点,与y轴交于点C , 其顶点为D , 连接AD .
(1)、求证:DE是⊙O的切线;(2)、若⊙O的半径为2, ,求CF的长.23. 如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c经过A(﹣3,0)、B(1,0)两点,与y轴交于点C , 其顶点为D , 连接AD .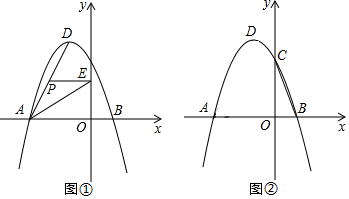 (1)、求抛物线的函数解析式;(2)、如图①,若点P是线段AD上一个动点,过点P作PE⊥y轴于点E , 求△PAE面积S的最大值;(3)、如图②,若点M是x轴上一个动点,过M作直线MQ∥BC交抛物线于点Q , 问抛物线上是否存在点Q , 使以点B、C、M、Q为顶点的四边形是平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的函数解析式;(2)、如图①,若点P是线段AD上一个动点,过点P作PE⊥y轴于点E , 求△PAE面积S的最大值;(3)、如图②,若点M是x轴上一个动点,过M作直线MQ∥BC交抛物线于点Q , 问抛物线上是否存在点Q , 使以点B、C、M、Q为顶点的四边形是平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由.