山西省临汾市翼城县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-10-13 类型:期末考试
一、单选题
-
1. 下列各式是最简二次根式的是( )A、 B、 C、 D、2. 已知关于x的一元二次方程x2+bx﹣1=0,则下列关于该方程根的判断,正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、实数根的个数与实数b的取值有关3. 在 中,AD是BC边上的中线,点G是重心,如果 ,那么线段DG的长为( )A、3 B、4 C、9 D、124. 如图,在 的正方形网格中,每个小正方形的边长都是 , 的顶点都在这些小正方形的顶点上,则 的值为( )
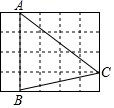 A、 B、 C、 D、5. 将抛物线 向左平移2个单位,再向下平移3个单位得到的抛物线是( )A、 B、 C、 D、6. 如图,△ABC与△DEF位似,点O为位似中心.已知OA∶OD=1∶2,则△ABC与△DEF的面积比为( )
A、 B、 C、 D、5. 将抛物线 向左平移2个单位,再向下平移3个单位得到的抛物线是( )A、 B、 C、 D、6. 如图,△ABC与△DEF位似,点O为位似中心.已知OA∶OD=1∶2,则△ABC与△DEF的面积比为( )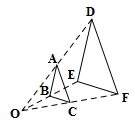 A、1∶2 B、1∶3 C、1∶4 D、1∶57. 如图, 是 的内接三角形, , ,AD是直径, ,则AC的长为( )
A、1∶2 B、1∶3 C、1∶4 D、1∶57. 如图, 是 的内接三角形, , ,AD是直径, ,则AC的长为( )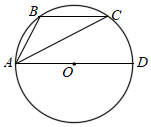 A、4 B、 C、 D、28. 一定滑轮的起重装置如图,滑轮半径为6cm,当重物上升 时,滑轮的一条半径OA按逆时针方向旋转的度数为(假设绳索与滑轮之间没有滑动)( )
A、4 B、 C、 D、28. 一定滑轮的起重装置如图,滑轮半径为6cm,当重物上升 时,滑轮的一条半径OA按逆时针方向旋转的度数为(假设绳索与滑轮之间没有滑动)( ) A、 B、 C、 D、9. 如图,在Rt△ABO中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得的阴影部分的面积为S,则S与t之间的函数关系式为( )
A、 B、 C、 D、9. 如图,在Rt△ABO中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得的阴影部分的面积为S,则S与t之间的函数关系式为( ) A、S=t(0<t≤3) B、S= t2(0<t≤3) C、S=t2(0<t≤3) D、S= t2-1(0<t≤3)10. 目前以 等为代表的战略性新兴产业蓬勃发展.某市2019年底有 用户2万户,计划到2021年底全市 用户数达到3.38万户,设全市用户数年平均增长率为x,则x值为( )A、20% B、30% C、40% D、50%
A、S=t(0<t≤3) B、S= t2(0<t≤3) C、S=t2(0<t≤3) D、S= t2-1(0<t≤3)10. 目前以 等为代表的战略性新兴产业蓬勃发展.某市2019年底有 用户2万户,计划到2021年底全市 用户数达到3.38万户,设全市用户数年平均增长率为x,则x值为( )A、20% B、30% C、40% D、50%二、填空题
-
11. 若二次根式 在实数范围内有意义,则x的取值范围为 .12. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用,如图是小明同学的健康码(绿码)示意图,用黑白打印机打印于边长为3cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 .
 13. 如图,铁道口的栏杆短臂长1m , 长臂长16m . 当短臂端点下降0.5m时,长臂端点升高
13. 如图,铁道口的栏杆短臂长1m , 长臂长16m . 当短臂端点下降0.5m时,长臂端点升高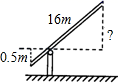 14. 如图,在 中, , ,以 为直径的 交BC于点D,若 ,则图中阴影部分的面积为 .
14. 如图,在 中, , ,以 为直径的 交BC于点D,若 ,则图中阴影部分的面积为 . 15. 二次函数 的图象如图所示,有下列结论:①当 时, ;② ;③ ;④ .其中,正确结论的序号是 .
15. 二次函数 的图象如图所示,有下列结论:①当 时, ;② ;③ ;④ .其中,正确结论的序号是 .
三、解答题
-
16.(1)、计算:(2)、解方程:17. 子怡的爸爸积极参加社区抗疫志愿服务工作,根据社区安排,志愿者被随机分到A组(体温检测)、B组(便民代购)和C组(环境消杀).(1)、子怡爸爸被分到B组的概率是;(2)、某中学李老师也参加了该社区的志愿者队伍,请用画树状图或列表的方法求李老师和子恰的爸爸被分到同组的概率是多少?18. 已知二次函数 .
 (1)、将二次函数化成 的形式;(2)、求二次函数图象与x轴的交点坐标;(3)、在平面直角坐标系中画出 的图象;(4)、结合函数图象,直接写出 时x的取值范围.19. 已知:如图, 的直径AB与弦CD相交于点E,且E为CD中点,过点B作CD的平行线交弦AD的延长线于点F.
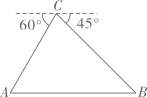
(1)、将二次函数化成 的形式;(2)、求二次函数图象与x轴的交点坐标;(3)、在平面直角坐标系中画出 的图象;(4)、结合函数图象,直接写出 时x的取值范围.19. 已知:如图, 的直径AB与弦CD相交于点E,且E为CD中点,过点B作CD的平行线交弦AD的延长线于点F.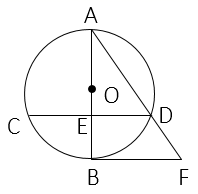 (1)、求证:BF是 的切线;(2)、连接BC,若 的半径为4, ,线段AD的长.20. 老李瓜果店销售一种进价为20元/千克的优质水果,若售价为30元/千克,则一个月可售出500千克;若售价在30元/千克的基础上每涨价1元,则月销售量就减少10千克.(1)、当售价为35元/千克时,每月销售水果多少千克?(2)、当老李瓜果店追求月利润为8640元时,又想让顾客得到实惠,每千克水果售价应为多少元?(3)、当每千克水果售价为多少元时,获得的月利润最大?最大利润是多少?21. 某校“综合与实践”小组采用无人机辅助的方法测量一座桥的长度.如图,桥 是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥 的上方120米的点C处悬停,此时测得桥两端A,B两点的俯角分别为60°和45°,求桥 的长度.
(1)、求证:BF是 的切线;(2)、连接BC,若 的半径为4, ,线段AD的长.20. 老李瓜果店销售一种进价为20元/千克的优质水果,若售价为30元/千克,则一个月可售出500千克;若售价在30元/千克的基础上每涨价1元,则月销售量就减少10千克.(1)、当售价为35元/千克时,每月销售水果多少千克?(2)、当老李瓜果店追求月利润为8640元时,又想让顾客得到实惠,每千克水果售价应为多少元?(3)、当每千克水果售价为多少元时,获得的月利润最大?最大利润是多少?21. 某校“综合与实践”小组采用无人机辅助的方法测量一座桥的长度.如图,桥 是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥 的上方120米的点C处悬停,此时测得桥两端A,B两点的俯角分别为60°和45°,求桥 的长度.
 22. 梅涅劳斯定理
22. 梅涅劳斯定理梅涅劳斯( )是古希腊数学家,他首先证明了梅涅劳斯定理,定理的内容是:
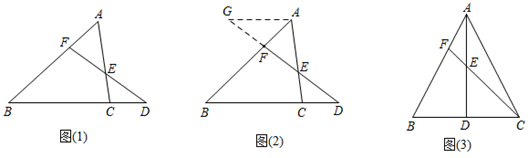
如图(1),如果一条直线与 的三边AB,BC,CA或它们的延长线交于F、D、E三点,那么一定有 .
下面是利用相似三角形的有关知识证明该定理的部分过程:
证明:如图(2),过点A作 ,交DF的延长线于点G,则有 .
任务:
(1)、请你将上述材料中的剩余的证明过程补充完整;(2)、如图(3),在 中, , ,点D为BC的中点,点F在AB上,且 ,CF与AD交于点E,则 .23. 如图,抛物线与x轴交于点 , ,与y轴交于点 .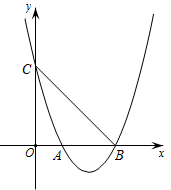
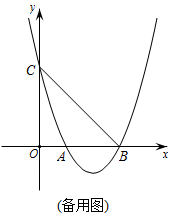 (1)、求二次函数的表达式及顶点坐标;(2)、若点P为抛物线上的一点,且 ,求点P的坐标;;(3)、连接BC,在抛物线的对称轴上是否存在一点E,使 是直角三角形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
(1)、求二次函数的表达式及顶点坐标;(2)、若点P为抛物线上的一点,且 ,求点P的坐标;;(3)、连接BC,在抛物线的对称轴上是否存在一点E,使 是直角三角形?若存在,请直接写出点E的坐标;若不存在,请说明理由.