山西省晋中市太谷县2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-10-13 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程是一元二次方程的是（）

A、y+x²﹣1＝0 B、x²+3＝0 C、x﹣3y+5＝0 D、2x﹣6＝ $\frac{1}{x}$

查看试题解析
2. 关于反比例函数 $y = - \frac{3}{x}$ ，下列各点在此双曲线上的是（）

A、（3，1） B、（ $\frac{1}{3}$ ，﹣3） C、（﹣1，﹣ $\frac{1}{3}$ ） D、（3，﹣1）

查看试题解析
3. 已知2是一元二次方程x²﹣c＝0的一个根，则该方程的另一个根是（　　）

A、﹣4 B、﹣2 C、2 D、4

查看试题解析
4. 在 $R t Δ A B C$ 中， $∠ C = 90^{\circ}$ ，如果 $∠ A$ 的正弦值是 $\frac{1}{4}$ ，那么下列各式正确的是（）

A、 $A B = 4 B C$ B、 $A B = 4 A C$ C、 $A C = 4 B C$ D、 $B C = 4 A C$

查看试题解析
5. 一个圆柱体钢块，正中央被挖去了一个长方体孔，其俯视图如图所示．则此圆柱体钢块的主视图可能是下列选项中的（）

A、 B、 C、 D、

查看试题解析
6. 箱子内装有除颜色外均相同的28个白球及2个红球，小芬打算从箱子内摸球，以每次摸到一球后记下颜色将球再放回的方式摸28次球．若箱子内每个球被摸到的机会相等，且前27次中摸到白球26次及红球1次，则第28次摸球时，小芬摸到红球的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{14}$ C、 $\frac{1}{15}$ D、 $\frac{1}{27}$

查看试题解析
7. 对抛物线：y＝x²+2x﹣3而言，下列结论正确的是（）

A、开口向下 B、顶点坐标是（1，﹣2） C、与x轴有两个交点 D、与y轴的交点是（0，3）

查看试题解析
8. 如图， $△ O E^{'} F^{'}$ 与 $△ O E F$ 关于原点O位似，相似比为 $1 ： 2$ ，已知 $E (- 4 ， 2)$ ， $F (- 1 ， - 1)$ ，则点E的对应点 $E^{'}$ 的坐标为（）

A、 $(2 ， 1)$ B、 $(\frac{1}{2} ， \frac{1}{2})$ C、 $(2 ， - 1)$ D、 $(2 ， - \frac{1}{2})$

查看试题解析
9. 如图，在平面直角坐标系xOy中，正方形ABCD的顶点D在y轴上，且A（﹣3，0），B（2，b），则b的值为（）

A、3 B、2 C、﹣3 D、﹣2

查看试题解析
10. 为了响应“绿水青山就是金山银山”的号召，建设生态文明，某工厂自2019年1月开始限产进行治污改造，其月利润y（万元）与月份x之间的变化如图所示，治污完成前是反比例函数图象的一部分，治污完成后是一次函数图象的一部分，下列选项正确的是（）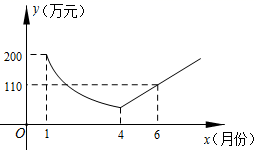

A、4月份的利润为50万元 B、治污改造完成后每月利润比前一个月增加30万元 C、治污改造完成前后共有3个月的利润低于100万元 D、8月份该厂利润达到200万元

查看试题解析

二、填空题

11. 如图，某河提进水坡AB的坡比 $i$ = 1： $\sqrt{3}$ ，堤高BC = 5 m，则坡面AB的长是 m．

查看试题解析
12. 如图，将一个装有水的杯子斜放在水平的桌面上，其截面可看作一个宽BC＝6厘米的矩形．当水面触到杯口边缘时，水面宽度BE＝12厘米，此时杯子的倾斜角α等于度．

查看试题解析

13. 已知二次函数y＝ax²＋bx＋c（a≠0）中，函数值y与自变量x的部分对应值如下表：

x	…	﹣5	﹣4	﹣3	﹣2	﹣1	…
y	…	0	﹣2	﹣5	﹣6	﹣5	…

则关于x的一元二次方程ax²＋bx＋c＝﹣2的根是．

查看试题解析

14. 若标有A，B，C的三只灯笼按图示悬挂，每次摘取一只（摘B先摘C），直到摘完，则最后一只摘到B的概率是．

查看试题解析
15. 如图，ABCD为正方形，O为AC、BD的交点，△DCE为直角三角形，∠CED＝90°，∠DCE＝30°，若正方形的边长为2，则OE的长为．

查看试题解析

三、解答题

16.

(1)、计算： $\sqrt{3}$ tan30°－ sin²30°－ $\sqrt{2}$ sin45°；

(2)、解方程：x²﹣6x+3＝0；

查看试题解析
17. 如图，直线y＝ $\frac{3}{2}$ x﹣3与反比例函数y＝ $\frac{k}{x}$ 相交于点 A（﹣2，m）、B（n ， 3）．

(1)、连接OA、OB ，求反比例函数关系式及△AOB的面积；

(2)、根据（1）中的图象信息，请直接写出不等式 $\frac{k}{x} > \frac{3}{2} x - 3$ 的解集．

查看试题解析
18. 某商场，为了吸引顾客，在“白色情人节”当天举办了商品有奖酬宾活动，凡购物满200元者，有两种奖励方案供选择：一是直接获得20元的礼金券，二是得到一次摇奖的机会．已知在摇奖机内装有2个红球和2个白球，除颜色外其它都相同，摇奖者必须从摇奖机内一次连续摇出两个球，根据球的颜色（如表）决定送礼金券的多少．
球
两红
一红一白
两白
礼金券（元）
18
24
18

(1)、请你用列表法（或画树状图法）求一次连续摇出一红一白两球的概率．

(2)、如果一名顾客当天在本店购物满200元，若只考虑获得最多的礼品券，请你帮助分析选择哪种方案较为实惠．

查看试题解析
19. 智能手机如果安装了一款测量软件后，就可以测量物高、宽度和面积等，如图，打开软件后将手机摄像头对准雕像底部按键，再对准雕像顶部按键，即可测量出雕像的高度．测量者AB所用数学原理如图②所示，测量者AB与雕像CD都垂直于地面BE ，若手机显示AC＝20m，AD＝32m，∠CAD＝37°，求此时雕像CD的高．（参考数据：sin37°≈ $\frac{3}{5}$ ，cos37°≈ $\frac{4}{5}$ ，tan37°≈ $\frac{3}{4}$ ）

查看试题解析
20. 请阅读下列材料，并完成相应的任务．

正方形网格是认识数和形的绝好途径．在网格中构造几何图形具有直观性和可操作性，网格中的数学问题具有显著的数形结合和转化的特征．下面网格图中每个小正方形的边长都为1．

如图1，点A、B、C、D都是格点，连接AC ， BD交于点O ，则AC ， BD互相平分．

如图2，点A、B、C、D都是格点，连接AC ， BD交于点M ，则点M是线段AC的四等分点．

任务一：请你观察图1，连接AD、DC、CB、AB ，则AC ， BD互相平分，其理由是 ▲ ．

任务二：请你观察图2，说明点M是AC的四等分点的理由．

任务三：在下面网格图中按要求作图．要求：①仅用无刻度直尺；②保留必要的思考痕迹．

在图3中的线段BC上做两点M、N ，使得△ABM与△ABN都为等腰三角形．

查看试题解析
21. 某商场以每件30元的价格购进一种商品，试销中发现这种商品每天的销售量m（件）与每件的销售价x（元）满足如图所示的线段表示的函数关系．

(1)、求商场卖这种商品每天的销售利润y（元）与每件销售价x（元）之间的函数关系式，并写出自变量的取值范围．

(2)、商场每天销售这种商品的销售利润能否达到500元？如果能，求出此时的销售价格；如果不能，说明理由．

查看试题解析
22. 综合实践
自主探究：

在课堂上，老师指导大家做以下活动：如图1，将已知矩形ABCD绕着点A顺时针旋转使得点D落在线段BC上，得到矩形AEFG ，连接DG交AE于点H ，在猜想线段HD与HG的关系时，大家一致认为HD=HG ，并且有两个小组给出如下的证明思路：

奋进组：要想证明HD=HG ，已经知道线段HG是直角三角形GAH的斜边，所以可以构造一个以HD为斜边的直角三角形，然后证明这两个三角形全等；

勤奋组：要想证明HD=HG ，可构造一个三角形，使得H、A分别在此三角形的两条边上，再证明HA是这个三角形的中位线；

操作思考：

(1)、请你在图1中分别作出符合“奋进组”和“勤奋组”思路需要的辅助线，并将辅助线的做法写在下面的横线上．
奋进组：．

勤奋组：．

(2)、请你根据“奋进组”和“勤奋组”提出的思路和作出的辅助线对下面问题做出选择（）

A、“奋进组”的思路正确，“勤奋组”的思路不正确 B、“勤奋组”的思路正确，“奋进组”的思路不正确 C、“奋进组”和“勤奋组”的思路都正确 D、“奋进组”和“勤奋组”的思路都不正确

(3)、变式证明：
将矩形ABCD绕着点A顺时针旋转使得点D落在线段CB的延长线上点E处，得到矩形AEFG ，连接DG交EA的延长线于点H，如图2，那么线段HD与HG还相等吗？说明理由．

(4)、将矩形ABCD绕着点A顺时针旋转使得点C落在线段CB的延长线上点F处，得到矩形AEFG ，连接DG交EA的延长线于点H ，且点C、A、G在同一直线上．如图3．问：线段HD与HG还相等吗？如果相等请直接写出 $\frac{A D}{A B}$ 的值；如果不相等，请说明理由．

查看试题解析
23. 综合探究
如图，直线y= $\frac{1}{2}$ x+c与x轴交于点A（-4，0），与y轴交于点B ，抛物线 $y = - \frac{1}{2} x^{2} + b x + c$ 经过点A、B ，与X轴的另一交点为C．已知动点M在直线AB上方的抛物线上，动点P在线段AB上．

(1)、求抛物线的解析式

(2)、连接AM、BM ，求△MAB的面积最大时点M的坐标．

(3)、连接MP、MB ，请直接写出当△BMP为等腰直角三角形时点P的坐标．

查看试题解析

球	两红	一红一白	两白
礼金券（元）	18	24	18