山西省晋城市2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-10-13 类型:期末考试
一、单选题
-
1. 若式子 有意义,则x的取值范围是( )A、x>1 B、x≥1 C、x≥0,x≠1 D、x>02. 下列函数是二次函数的是( )A、 B、 C、 D、3. 一元二次方程x2﹣3x+4=0的根的情况是( )A、有两个不相等的实数 B、有两个相等的实数根 C、没有实数根 D、无法判断4. 如图, ,下列各式错误的是( )
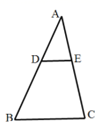 A、 B、 C、 D、5. 在两个袋内,分别装着写有1、2、3、4四个数字的4张卡片,卡片除数字外其余都相同,今从每个袋中各任取一张卡片,则所取两卡片上数字之积为偶数的概率是( )A、 B、 C、 D、6. 下列说法正确的是( )A、圆的任意一条直径都是它的对称轴 B、相等的圆心角所对的弧相等 C、平分弦的直径垂直于弦 D、圆中最长的弦是直径7. 将抛物线y=x2﹣2向右平移3个单位长度,再向上平移2个单位长度,则所得抛物线的解析式为( )A、y=(x+3)2 B、y=(x﹣3)2 C、y=(x+2)2+1 D、y=(x﹣2)2+18. 如图, 是 的直径, 是 上的三等分点,且 ,则 等于 ( )
A、 B、 C、 D、5. 在两个袋内,分别装着写有1、2、3、4四个数字的4张卡片,卡片除数字外其余都相同,今从每个袋中各任取一张卡片,则所取两卡片上数字之积为偶数的概率是( )A、 B、 C、 D、6. 下列说法正确的是( )A、圆的任意一条直径都是它的对称轴 B、相等的圆心角所对的弧相等 C、平分弦的直径垂直于弦 D、圆中最长的弦是直径7. 将抛物线y=x2﹣2向右平移3个单位长度,再向上平移2个单位长度,则所得抛物线的解析式为( )A、y=(x+3)2 B、y=(x﹣3)2 C、y=(x+2)2+1 D、y=(x﹣2)2+18. 如图, 是 的直径, 是 上的三等分点,且 ,则 等于 ( )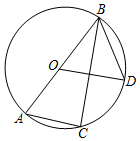 A、120° B、95° C、105° D、150°9. 如图,在 中,D是 上一点,连接 是 的中点,连接 并延长交 于点E , 则 的值为( )
A、120° B、95° C、105° D、150°9. 如图,在 中,D是 上一点,连接 是 的中点,连接 并延长交 于点E , 则 的值为( )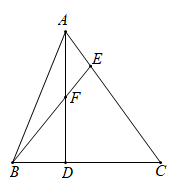 A、 B、 C、 D、10. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②4a+2b+c>0;③(a+c)2>b2;④2c<3b;⑤a+b>m(am+b)(m≠1的实数).其中正确的结论有( )
A、 B、 C、 D、10. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②4a+2b+c>0;③(a+c)2>b2;④2c<3b;⑤a+b>m(am+b)(m≠1的实数).其中正确的结论有( )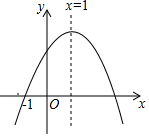 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 计算: .12. 已知二次函数 的函数值y与自变量x的部分对应值如下表:
x
…
0
1
2
3
…
y
…
8
3
0
0
3
…
则这个二次函数的图象的顶点坐标是 .
13. 如图,在矩形 中, ,点P在 上(不与 两点重合),当 时, . 14. 如图, 是 的两条相交弦, ,则 的直径是 .
14. 如图, 是 的两条相交弦, ,则 的直径是 .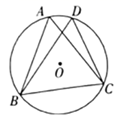
三、解答题
-
15. 在平面直角坐标系中, , ,经过原点的直线 上有一点 ,平移线段 ,对应线段为 ( 对应 ),若点 、 分别恰好在直线 和 轴上,则 点坐标为 .
 16.(1)、用配方法解方程: .(2)、计算: .17. 计算: .18. 小兰和小英周末都想去看电影,但只有一张电影票,二人决定做游戏,谁获胜谁就去看电影.游戏规则如下:在一只不透明的口袋中有除所标数字外完全相同的4张卡片,卡片上分别写有数字 ,现从口袋中随机取出两张卡片,如果取出的两张卡片上的数字之积为负数,那么小兰获胜,小兰就去看电影,否则,小英去看电影.(1)、用画树状图或列表的方法求出小兰去看电影的概率.(2)、小英说:“这种规则不公平.”你认为小英的说法正确吗?请说明理由.19. 某水果店购进一批优质水果,进价为10元/千克,售价不低于15元/千克,且不超过40元/每千克,根据销售情况,发现该水果在一天内的销售量x(千克)与该天的售价 (元/千克)之间的数量满足如下表所示的一次函数关系.
16.(1)、用配方法解方程: .(2)、计算: .17. 计算: .18. 小兰和小英周末都想去看电影,但只有一张电影票,二人决定做游戏,谁获胜谁就去看电影.游戏规则如下:在一只不透明的口袋中有除所标数字外完全相同的4张卡片,卡片上分别写有数字 ,现从口袋中随机取出两张卡片,如果取出的两张卡片上的数字之积为负数,那么小兰获胜,小兰就去看电影,否则,小英去看电影.(1)、用画树状图或列表的方法求出小兰去看电影的概率.(2)、小英说:“这种规则不公平.”你认为小英的说法正确吗?请说明理由.19. 某水果店购进一批优质水果,进价为10元/千克,售价不低于15元/千克,且不超过40元/每千克,根据销售情况,发现该水果在一天内的销售量x(千克)与该天的售价 (元/千克)之间的数量满足如下表所示的一次函数关系.销售量(千克)
…
32.5
35
35.5
38
…
售价(元/千克)
…
27.5
25
24.5
22
…
(1)、某天这种水果售价为28元/千克,求当天该芒果的销售量;(2)、如果水果店该天获利400元,那么这天水果的售价为多少元?20. 如图,一艘渔船位于小岛 的北偏东 方向,距离小岛 的点 处,它沿着点 的南偏东 的方向航行. (1)、渔船航行多远距离小岛 最近(结果保留根号)?(2)、渔船到达距离小岛 最近点后,按原航向继续航行 到点 处时突然发生事故,渔船马上向小岛 上的救援队求救,问救援队从 处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少(结果保留根号)?21. 景德桥,俗称西关大桥,是我国一座著名的古代石拱桥.景德桥位于山西省东南部的晋城西门外,横跨沁水河,过去,它是晋城通往沁水河阳城地区交通干道上的一座重要桥梁,故曾又名沁阳桥.桥下水面宽度 是20米,拱高 是4米,若水面上升3米至 处.
(1)、渔船航行多远距离小岛 最近(结果保留根号)?(2)、渔船到达距离小岛 最近点后,按原航向继续航行 到点 处时突然发生事故,渔船马上向小岛 上的救援队求救,问救援队从 处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少(结果保留根号)?21. 景德桥,俗称西关大桥,是我国一座著名的古代石拱桥.景德桥位于山西省东南部的晋城西门外,横跨沁水河,过去,它是晋城通往沁水河阳城地区交通干道上的一座重要桥梁,故曾又名沁阳桥.桥下水面宽度 是20米,拱高 是4米,若水面上升3米至 处.
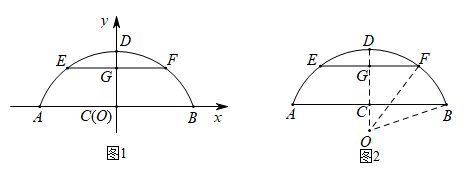 (1)、把拱桥看作抛物线的一部分,建立如图1所示的平面直角坐标系,求水面宽度 .(2)、把拱桥看作圆的一部分,则可构造如图2所示的图形,求水面宽度 .22. 问题提出:如图,在锐角 中,如何作一个正方形 ,使 落在 边上, 分别落在 边上?
(1)、把拱桥看作抛物线的一部分,建立如图1所示的平面直角坐标系,求水面宽度 .(2)、把拱桥看作圆的一部分,则可构造如图2所示的图形,求水面宽度 .22. 问题提出:如图,在锐角 中,如何作一个正方形 ,使 落在 边上, 分别落在 边上?勤奋小组同学给出了如下作法:①画一个有三个顶点落在 两边上的正方形 ;
②连接 ,并延长交 于点 ;③过点 作 于点 ;④过 作 ,交 于点 ;⑤过点 作 于点 ,则四边形 即为所求作的正方形.
受勤奋小组同学的启发,创新小组同学认为可以在锐角 中,作出长与宽的比为 的矩形 ,使 位于边 上, 分别位于边 上.
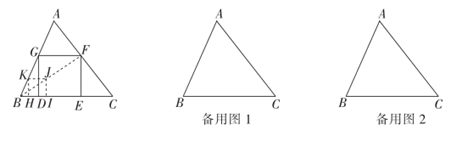 (1)、你认为勤奋小组同学的作法正确吗?请说明理由.(2)、请你帮助创新小组同学在在锐角 中,作出所有满足长与宽的比为 的矩形 ,使 位于边 上, 分别位于边 上.(在备用图中完成,不写作法,保留作图痕迹)
(1)、你认为勤奋小组同学的作法正确吗?请说明理由.(2)、请你帮助创新小组同学在在锐角 中,作出所有满足长与宽的比为 的矩形 ,使 位于边 上, 分别位于边 上.(在备用图中完成,不写作法,保留作图痕迹)解决问题:
(3)、在(2)的条件下,已知 的面积为36, ,求出矩形 的面积.23. 综合与探究:如图,抛物线 与x轴交于 两点(点A在点B的左边),与直线 分别交于 两点,P为抛物线上一动点,过点P作 轴于点D , 交直线 于点E .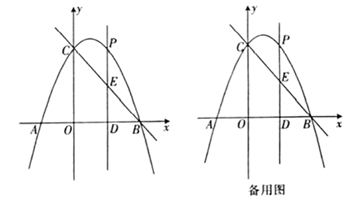 (1)、求抛物线的表达式.(2)、若点E在线段 上,求线段 长度的最大值.(3)、连接 ,当 时,求点P的坐标.
(1)、求抛物线的表达式.(2)、若点E在线段 上,求线段 长度的最大值.(3)、连接 ,当 时,求点P的坐标.