山西省大同市浑源县2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-10-13 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程 $x^{2} - 9 = 0$ 的解是（）

A、 $x = 3$ B、 $x = - 3$ C、 $x_{1} = 3$ ， $x_{2} = - 3$ D、 $x_{1} = 9$ ， $x_{2} = - 9$

查看试题解析
2. 云纹，指云形纹饰，是古代中国吉祥图案，象征高升和如意，被广泛地运用于装饰中．下列的云纹图案中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 现有4张扑克牌（除牌面花色外完全相同）：2张红桃 $A$ 、1张黑桃 $A$ 、1张梅花 $A$ ，将它们洗匀后背面朝上放置．现从中任意抽取一张牌，则抽到红桃 $A$ 的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、1

查看试题解析
4. 用配方法解一元二次方程 $x^{2} - 8 x + 9 = 0$ ，变形后的结果正确的是（）

A、 ${(x - 4)}^{2} = - 7$ B、 ${(x - 4)}^{2} = 7$ C、 ${(x + 4)}^{2} = 7$ D、 ${(x - 4)}^{2} = 25$

查看试题解析
5. 如图， $△ A B C$ 是 $⊙ O$ 的内接三角形，若 $∠ A B C = 60 °$ ，则 $∠ A O C$ 的大小是（）

A、30° B、120° C、135° D、150°

查看试题解析
6. 一元二次方程 $2 x^{2} - x - 1 = 0$ 的根的情况为（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
7. 在平面直角坐标系内，将抛物线 $y = {(x + 2)}^{2} - 3$ 经过两次平移后，得到的新抛物线为 $y = {(x - 1)}^{2} - 4$ .下列对这一平移过程描述正确的是（）

A、先向右平移3个单位长度，再向下平移1个单位长度 B、先向左平移3个单位长度，再向下平移1个单位长度 C、先向右平移3个单位长度，再向上平移1个单位长度 D、先向左平移3个单位长度，再向下平移1个单位长度

查看试题解析
8. 学校准备举办“和谐校园”摄影作品展黛，现要在一幅长 $30 cm$ ，宽 $20 cm$ 的矩形作品四周外围上宽度相等的彩纸，并使彩纸的面积恰好与原作品面积相等，设彩纸的宽度为 $x cm$ ，则 $x$ 满足的方程是（）

A、 $(30 + 2 x) (20 + 2 x) = 30 \times 20$ B、 $(30 + x) (20 + x) = 30 \times 20$ C、 $(30 - 2 x) (20 - 2 x) = 2 \times 30 \times 20$ D、 $(30 + 2 x) (20 + 2 x) = 2 \times 30 \times 20$

查看试题解析
9. 如图是抛物线 $y = a x^{2} + b x + c$ 的一部分，其对称轴为直线 $x = - 1$ .已知该抛物线过点 $(- 3 ， 0)$ ，则下列判断正确的是（）

A、 $a b c < 0$ B、 $2 a + b = 0$ C、该抛物线过点 $(1 ， 0)$ D、当 $x < 0$ 时， $y$ 随 $x$ 的增大而增大

查看试题解析
10. 德国数学家高斯在大学二年级时得出了正十七边形的尺规作图法，并给出了可用尺规作图的正多边形的条件，下面是高斯正十七边形作法的一部分：已知 $A B$ 是 $⊙ O$ 的直径．分别以 $A$ ， $B$ 为圆心、 $A B$ 长为半径作弧，两弧交于点 $C$ ， $D$ 两点．…若设 $A B$ 长为2，则图中阴影部分的面积为（）

A、 $\frac{5}{3} π - 2 \sqrt{3}$ B、 $\frac{8}{3} π - 2 \sqrt{3}$ C、 $\frac{5}{3} π - \sqrt{3}$ D、 $\frac{8}{3} π - 4 \sqrt{3}$

查看试题解析

二、填空题

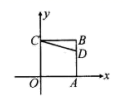
11. 用分解因式法解一元二次方程 $(4 x - 1) (x + 3) = 0$ 时，可将原方程转化为两个一元一次方程，其中一个方程是 $4 x - 1 = 0$ ，则另一个方程是．

查看试题解析
12. 如图，正方形 $O A B C$ 的两边 $O A$ 、 $O C$ 分别在 $x$ 轴、 $y$ 轴上，点 $D (5 ， 3)$ 在边 $A B$ 上，以 $C$ 为中心，把 $△ C D B$ 顺时针旋转90°，则旋转点 $D$ 的对应点 $D^{'}$ 的坐标是．

查看试题解析
13. 如图， $A B$ 是 $⊙ O$ 的直径， $C D$ 是 $⊙ O$ 的弦，连接 $A C$ 、 $A D$ ，若 $∠ C A B = 40 °$ ，则 $∠ A D C$ 的度数为．

查看试题解析
14. 如图，小彬收集了三张除正面图案外完全相同的卡片，其中两张印有嫦娥5号在月面自动采样的卡通图，另外一张印有嫦娥5号首次从月面起飞的示意图，现将三张卡片背面朝上放置，搅匀后从中一次性随机抽取两张，则抽到的两张卡片图案不相同的概率为．

查看试题解析
15. 如图，已知正方形 $A B C D$ ，将边 $C D$ 绕点 $C$ 顺时针旋转45°，得到线段 $C E$ ，连接 $D E$ 、 $A E$ ， $D C = 2$ ，则 $A E$ 的长为．

查看试题解析

三、解答题

16.

(1)、解方程： $x^{2} + 6 x - 5 = 0$ ；

(2)、阅读下解方程的过程，并解决问题：
解：方程右边分解因式，得 $3 x (x - 5) = 2 (5 - x)$ …………………（第一步）

方程变形为 $3 x (x - 5) = - 2 (x - 5)$ ……………………………（第二步）

方程两边都除以 $x - 5$ ，得 $3 x = - 2$ …………………………………（第三步）

解，得 $x = - \frac{2}{3}$ .………………………………………………………（第四步）

①上述解方程的过程从第步开始出错，具体的错误是．

②请直接写出方程的根．

查看试题解析
17. 已知二次函数 $y = x^{2} - 4 x + 3$ ．

(1)、将二次函数表达式 $y = x^{2} - 4 x + 3$ 化成 $y = a {(x - h)}^{2} + k$ 的形式，并直接写出其顶点坐标；

(2)、完成下列表格并在如图所示的直角坐标系内画出该函数的大致图像；

$x$

…

0

1

2

3

4

$y = x^{2} - 4 x + 3$

…

(3)、根据图象直接回答：当 $x$ 时， $y$ 随 $x$ 的增大而减小；当 $y < 0$ 时， $x$ 的取值范围是．

查看试题解析
18. 2019年11月1日5G商用套餐正式上线. 某移动营业厅为了吸引用户，设计了A，B两个可以自由转动的转盘(如图)，A转盘被等分为2个扇形，分别为红色和黄色；B转盘被等分为3个扇形，分别为黄色、红色、蓝色，指针固定不动. 营业厅规定，每位5G新用户可分别转动两个转盘各一次，转盘停止后，若指针所指区域颜色相同，则该用户可免费领取100G通用流量(若指针停在分割线上，则视其指向分割线右侧的扇形). 小王办理5G业务获得一次转转盘的机会，求他能免费领取100G通用流量的概率.

查看试题解析
19. 如图，在 $Δ A B C$ 中， $A F ⊥ B C$ 于点 $F$ ．将 $Δ A B C$ 绕点 $A$ 按顺时针旋转一定角度得到 $Δ A D E$ ，点 $B$ 的对应点 $D$ 恰好落在 $B C$ 边上．

(1)、若 $∠ B = 50^{°}$ ，求 $∠ D A F$ 的度数；

(2)、若 $∠ E = ∠ C A D$ ，求证： $A D = C D$ ．

查看试题解析
20. 2021元旦前夕，某花店购进一批单价为4元/枝的玫瑰，按每枝10元的价格销售，每天能售出80枝．经市场调查发现这种玫瑰的销售单价每降低1元，平均每天就能多售出40枝．

(1)、店家在每枝10元的基础上，将这种玫瑰的销售单价降低 $x$ 元，则平均每天的销售量为枝（用含 $x$ 的代数式表示）；

(2)、为了吸引顾客前来购买这种玫瑰需要采用更低的价格，并使得销售玫瑰每天的利润达到600元，则店家应将其销售单价降低多少元？

(3)、当这种玫瑰的销售单价降低多少元时，才能使该花店销售玫瑰每天所获利润最大？最大利润是多少？

查看试题解析
21. 如图， $△ A B C$ 内接于 $⊙ O$ ，且 $A B$ 为 $⊙ O$ 的直径，过点 $C$ 作 $⊙ O$ 的切线 $C D$ 交 $A B$ 的延长线于点 $D$ ，点 $E$ 在直径 $A B$ 上，且 $D E = D C$ ，连接 $C E$ 并延长交 $⊙ O$ 于点 $F$ .连接 $A F$ ， $B F$ ，试判断 $A F$ 与 $B F$ 的数量关系，并说明理由．

查看试题解析
22. 综合与实践——探究正方形旋转中的数学问题
问程情境：

已知正方形 $A B C D$ 中，点 $O$ 是线段 $B C$ 的中点，将将正方形 $A B C D$ 绕点 $O$ 顺时针旋转得到正方形 $A^{'} B^{'} C^{'} D^{'}$ （点 $A^{'}$ ， $B^{'}$ ， $C^{'}$ ， $D^{'}$ 分别是点 $A$ ， $B$ ， $C$ ， $D$ 的对应点）．同学们通过小组合作，提出下列数学问题，请你解答．

(1)、特例分析：
“乐思”小组提出问题：如图1，在正方形绕点 $O$ 旋转过程中，顺次连接点 $B$ ， $B^{'}$ ， $C$ ， $C^{'}$ 得到四边形 $B B^{'} C C^{'}$ ，求证：四边形 $B B^{'} C C^{'}$ 是矩形；

(2)、“善学”小组提出问题：如图2.在旋转过程中，当点 $B^{'}$ 落在对角线 $B D$ 上时，设 $A^{'} B^{'}$ 与 $C D$ 交于点 $M$ .求证：四边形 $O B^{'} M C$ 是正方形．

(3)、深入探究：
“好问”小组提出问题：如图3.若点 $O$ 是线段 $B C$ 的三等分点且 $O B = 2 O C$ ，在正方形 $A B C D$ 旋转的过程中当线段 $A^{'} D^{'}$ 经过点 $D$ 时，请直接写出 $\frac{D D^{'}}{O C^{'}}$ 的值．

查看试题解析
23. 综合与探究
如图1，抛物线 $y = - \frac{1}{2} x^{2} + b x + c$ 与 $y$ 轴交于点 $A$ ，直线 $y = - \frac{1}{2} x + 2$ 经过点 $A$ ，与 $x$ 轴交与点 $B$ ，且与抛物线的另一交点 $C$ 的横坐标为5．

(1)、求点 $A$ 、 $C$ 的坐标和抛物线的函数表达式；

(2)、将 $△ A O B$ 沿 $y$ 轴向上平移到 $△ A^{'} O^{'} B^{'}$ ，点 $O^{'}$ 恰好与点 $A$ 重合，点 $B$ 的对应点为点 $B^{'}$ ，判断点 $B^{'}$ 是否在抛物线上，说明理由；

(3)、如图2，点 $P$ 是直线 $A C$ 上方的抛物线上的一个动点，那么平面直角坐标系内是否存在一点 $Q$ ，使以点 $A$ 、 $C$ 、 $P$ 、 $Q$ 为顶点的平行四边形面积最大？如果存在，求出点 $P$ 的坐标，并直接写出点 $Q$ 的坐标；如果不存在，请说明理由．

查看试题解析

$x$	…	0	1	2	3	4
$y = x^{2} - 4 x + 3$	…