云南省文山壮族苗族自治州砚山县2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-10-13 类型:期末考试
一、填空题
-
1. 如图,学校有一块长方形草坪,有极少数人为了避开拐角走“捷径”,在草坪内走出了一条“路”,他们仅仅少走了步路(假设2步为1米),却踩伤了花草.
 2. 若代数式 有意义,则 的取值范围为.3. 如图,直线 , ,则 .
2. 若代数式 有意义,则 的取值范围为.3. 如图,直线 , ,则 .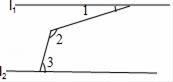 4. 甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地后,立即按原路以相同速度匀速返回(停留时间不作考虑),直到两车相遇.若甲、乙两车之间的距离y(千米)与两车行驶的时间x(小时)之间的函数图象如图所示,则A,B两地之间的距离为千米.
4. 甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地后,立即按原路以相同速度匀速返回(停留时间不作考虑),直到两车相遇.若甲、乙两车之间的距离y(千米)与两车行驶的时间x(小时)之间的函数图象如图所示,则A,B两地之间的距离为千米.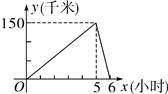 5. 在如图所示的平面直角坐标系中,点P是直线 上的动点, ,B(2,0)是x轴上的两点,则 的最小值为 .
5. 在如图所示的平面直角坐标系中,点P是直线 上的动点, ,B(2,0)是x轴上的两点,则 的最小值为 .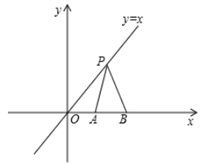 6. 如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为(用n表示)
6. 如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为(用n表示)
二、单选题
-
7. 估计5 ﹣ 的值应在( )A、5和6之间 B、6和7之间 C、7和8之间 D、8和9之间8. 两名同学进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学成绩哪一位更稳定,通常还需要比较他们成绩的( )A、众数 B、中位数 C、方差 D、以上都不对9. 两个一次函数 与 ,它们在同一直角坐标系中的图象可能是( )A、
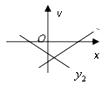 B、
B、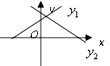 C、
C、 D、
D、 10. 三角形的一个外角等于与它相邻内角的4倍,等于与它不相邻的一个内角的2倍,则此三角形各角度数为( )A、 B、 C、 D、11. 关于x,y的方程组 的解是 ,其中y的值被盖住了,不过仍能求出p,则p的值是( )A、- B、 C、- D、12. 如图,已知△ABC≌△ADC,∠B=30°,∠BAC=23°,则∠ACD的度数为( )
10. 三角形的一个外角等于与它相邻内角的4倍,等于与它不相邻的一个内角的2倍,则此三角形各角度数为( )A、 B、 C、 D、11. 关于x,y的方程组 的解是 ,其中y的值被盖住了,不过仍能求出p,则p的值是( )A、- B、 C、- D、12. 如图,已知△ABC≌△ADC,∠B=30°,∠BAC=23°,则∠ACD的度数为( )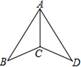 A、120° B、125° C、127° D、104°13. 如图,把矩形 沿 对折后使两部分重合,若 ,则 =( )
A、120° B、125° C、127° D、104°13. 如图,把矩形 沿 对折后使两部分重合,若 ,则 =( )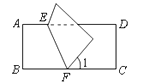 A、110° B、115° C、120° D、130°14. 实数a、b在数轴上的位置如图,则化简 的结果是( )
A、110° B、115° C、120° D、130°14. 实数a、b在数轴上的位置如图,则化简 的结果是( ) A、0 B、-2a C、2b D、-2a+2b
A、0 B、-2a C、2b D、-2a+2b三、解答题
-
15. 计算: .16. 如图是一块地,已知AD=4,CD=3,AB=13,BC=12,且CD⊥AD,求这块地的面积.
 17. 如图,在平面直角坐标系中, 的三个顶点坐标为, , , .
17. 如图,在平面直角坐标系中, 的三个顶点坐标为, , , . (1)、求 的面积.(2)、在图中作出 关于x轴对称的图形 ,并写出D,E,F的坐标.(A,B,C的对应点分别为D,E,F)18.
(1)、求 的面积.(2)、在图中作出 关于x轴对称的图形 ,并写出D,E,F的坐标.(A,B,C的对应点分别为D,E,F)18.“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
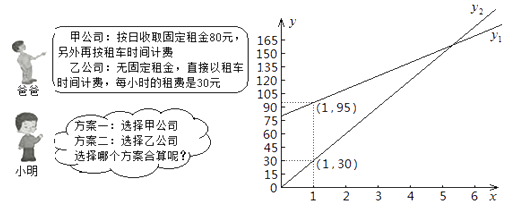
根据以上信息,解答下列问题:
(1)、设租车时间为 小时,租用甲公司的车所需费用为 元,租用乙公司的车所需费用为 元,分别求出 , 关于 的函数表达式;(2)、请你帮助小明计算并选择哪个出游方案合算。19. 如图,EF∥AD , AD∥BC , CE平分∠BCF , ∠DAC=120°,∠ACF=20°,求∠FEC的度数.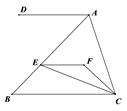 20. 州教育局为了解我州八年级学生参加社会实践活动情况,随机抽查了某县部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据检测了两幅统计图,下面给出了两幅不完整的统计图(如图)
20. 州教育局为了解我州八年级学生参加社会实践活动情况,随机抽查了某县部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据检测了两幅统计图,下面给出了两幅不完整的统计图(如图)
请根据图中提供的信息,回答下列问题:
(1)、a= , 并写出该扇形所对圆心角的度数为 , 请补全条形图.(2)、在这次抽样调查中,众数和中位数分别是多少?(3)、如果该县共有八年级学生2000人,请你估计“活动时间不少于7天”的学生人数大约有多少人?21. 如图,在平面直角坐标系中,存在直线 和直线 . (1)、求出直线 和直线 的交点坐标;(2)、结合图象,直接写出 的解集: .22. 某水果店11月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.12月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.(1)、若该店12月份购进这两种水果的数量与11月份都相同,将多支付货款300元,求该店11月份购进甲、乙两种水果分别是多少千克?(2)、若12月份将这两种水果进货总量减少到120千克,设购进甲种水果a千克,需要支付的货款为w元,求w与a的函数关系式;(3)、在(2)的条件下,若甲种水果不超过90千克,则12月份该店需要支付这两种水果的货款最少应是多少元?23. 如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点N沿路线O→A→C运动.
(1)、求出直线 和直线 的交点坐标;(2)、结合图象,直接写出 的解集: .22. 某水果店11月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.12月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.(1)、若该店12月份购进这两种水果的数量与11月份都相同,将多支付货款300元,求该店11月份购进甲、乙两种水果分别是多少千克?(2)、若12月份将这两种水果进货总量减少到120千克,设购进甲种水果a千克,需要支付的货款为w元,求w与a的函数关系式;(3)、在(2)的条件下,若甲种水果不超过90千克,则12月份该店需要支付这两种水果的货款最少应是多少元?23. 如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点N沿路线O→A→C运动. (1)、求直线AB的解析式.(2)、求△OAC的面积.(3)、当△ONC的面积是△OAC面积的 时,求出这时点N的坐标.
(1)、求直线AB的解析式.(2)、求△OAC的面积.(3)、当△ONC的面积是△OAC面积的 时,求出这时点N的坐标.