云南省昆明市盘龙区2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-10-13 类型：期末考试

进入出卷网下载

一、填空题

1. 因式分解： $3 x^{2} - 12 =$ .

查看试题解析
2. 若 $\frac{\sqrt{x}}{x - 3}$ 有意义，则x的取值范围是．

查看试题解析
3. 如果将一副三角板按如图方式叠放，那么∠1的大小为．

查看试题解析
4. 已知一个n边形的内角和等于1980°，则n= ．

查看试题解析
5. 若 $a 、 b 、 c$ 为三角形的三边，且 $a 、 b$ 满足 $\sqrt{a - 10} + {(b - 2)}^{2} = 0$ ，第三边c为偶数，则c＝.

查看试题解析
6. 已知，等腰△ABC中，AB=AC，∠BAC=120°，P为直线BC上一点，BP=AB，则∠APB的度数为 .

查看试题解析

二、单选题

7. 如图，四个图标中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
8. 2019年末，在中国武汉引发疫情的冠状病毒，被命名为 $COVID - 19$ 新型冠状病毒，冠状病毒的平均直径约是0.00000009米，数据0.00000009科学记数法表示为（）

A、 $0.9 \times 10^{- 8}$ B、 $9 \times 10^{- 8}$ C、 $9 \times 10^{- 7}$ D、 $0.9 \times 10^{- 7}$

查看试题解析
9. 下列运算正确的是（　　）

A、（x+y）²＝x²+y² B、（﹣ $\frac{1}{2}$ x²）³＝﹣ $\frac{1}{6}$ x⁶ C、 $\frac{1}{5^{- 2}}$ ＝ $\frac{1}{25}$ D、 $\sqrt{{(- 5)}^{2}}$ ＝5

查看试题解析
10. 现代科技的发展已经进入到了5G时代，温州地区将在2021年基本实现5G信号全覆盖.5G网络峰值速率为4G网络峰值速率的10倍，在峰值速率下传输4千兆数据，5G网络比4G网络快360秒.若设4G网络的峰值速率为每秒传输x千兆数据，则由题意可列方程（）

A、 $\frac{4}{10x}$ — $\frac{4}{x}$ =360 B、 $\frac{4}{x}$ — $\frac{4}{10x}$ =360 C、 $\frac{40}{x}$ — $\frac{4}{x}$ =360 D、 $\frac{4}{x}$ — $\frac{40}{x}$ =360

查看试题解析
11. 如图，∠CAB=∠DBA，再添加一个条件，不一定能判定△ABC≌△BAD的是（）

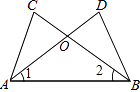A、AC=BD B、∠1=∠2 C、AD=BC D、∠C=∠D

查看试题解析
12. 能够用如图中已有图形的面积说明的等式是（）

A、a（a+4）＝a²+4a B、（a+4）（a﹣4）＝a²﹣16 C、（a+2）（a﹣2）＝a²﹣4 D、（a+2）²＝a²+4a+4

查看试题解析
13. 如图，在△ABC中，分别以点A和点B为圆心，以相同的长（大于 $\frac{1}{2}$ AB）为半径作弧，两弧相交于点M和点N，作直线MN交AB于点D，交AC于点E，连接CD．已知△CDE的面积比△CDB的面积小5，则△ADE的面积为（　　）

A、5 B、4 C、3 D、2

查看试题解析
14. 如图，已知△ABC中，AB＝AC ， ∠BAC＝90°，直角∠EPF的顶点P是BC中点，当∠EPF在△ABC内绕顶点P旋转时（点E不与A、B重合）两边PE、PF分别交AB、AC于点E、F ，给出以下四个结论：①AE＝CF；②△EPF是等腰直角三角形；③S_{四边形AEPF}＝ $\frac{1}{2}$ S_△ABC；④BE+CF＝EF ．上述结论始终正确的个数是（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

三、解答题

15. 计算：

(1)、8a⁶÷2a²﹣4a³•3a﹣（4a²）²；

(2)、（3 $\sqrt{12}$ ﹣2 $\sqrt{\frac{1}{3}} + \sqrt{48}$ ）÷2 $\sqrt{3}$ ．

查看试题解析
16. 先化简，再求值： $(\frac{m^{2} - 9}{m^{2} - 6 m + 9} - \frac{3}{m - 3}) \div \frac{m^{2}}{m - 3}$ ，其中 $m = \sqrt{2}$ .

查看试题解析
17. 如图，已知C是线段AE上的一点，DC⊥AE，DC=AC，B是CD上一点，且CB=CE．

(1)、△ABC与△DEC全等吗？请说明理由．

(2)、若∠A=20°，求∠E的度数．

查看试题解析
18. 解方程： $\frac{2 x}{x + 1} = 1 - \frac{x}{3 x + 3}$ ．

查看试题解析
19. 如图，在所给网格图（每小格均为边长是1的正方形）中完成下列各题：

⑴画出格点△ABC（顶点均在格点上）关于直线DE对称的△A₁B₁C₁；

⑵在DE上画出点Q，使 $Q A + Q C$ 最小．

⑶四边形BCC₁B₁的面积为 ▲ ．

查看试题解析
20. 甲、乙两个长方形的边长如图所示（m为正整数），其面积分别为 $S_{1}$ ， $S_{2}$ ．

(1)、请比较 $S_{1}$ 和 $S_{2}$ 的大小；

(2)、若一个正方形的周长等于甲、乙两个长方形的周长之和，求该正方形的面积（用含m的代数式表示）．

查看试题解析
21. 倡导健康生活推进全民健身，某社区去年购进A，B两种健身器材若干件，经了解，B种健身器材的单价是A种健身器材的1.5倍，用7200元购买A种健身器材比用5400元购买B种健身器材多10件.

(1)、A，B两种健身器材的单价分别是多少元？

(2)、若今年两种健身器材的单价和去年保持不变，该社区计划再购进A，B两种健身器材共50件，且费用不超过21000元，请问：A种健身器材至少要购买多少件？

查看试题解析
22. 如图，已知Rt△ABC中，∠ACB＝90°，CD⊥AB于点D ， ∠BAC的平分线分别交BC ， CD于点E、F ．

(1)、试说明△CEF是等腰三角形；

(2)、若点E恰好在线段AB的垂直平分线上，猜想：线段AC与线段AB的数量关系，并说明理由；

(3)、在（2）的条件下，若AC＝2.5，求△ABE的面积．

查看试题解析
23. 在平面直角坐标系中，直线AB分别交x轴，y轴于A（a ， 0），B（0，b），且满足 $\sqrt{a + 2}$ +b²﹣8b+16＝0．

(1)、求a ， b的值；

(2)、点P在直线AB的右侧，且∠APB＝45°．
①若点P在x轴上（图1），求点P的坐标；

②若△ABP为直角三角形，求P点的坐标．

查看试题解析