云南省昆明市官渡区2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-10-13 类型:期末考试
一、填空题
-
1. 要使分式 有意义,则x的取值范围为 .2. 云南的高黎贡山以其独特的地理地貌和丰富的动植物资源著称于世.在高黎贡山生长着中国特有树种——毛杉,它的种子十分细小,重量很轻,一粒种子仅有0.0015克.用科学记数法表示这个种子的质量为克.3. 计算 .4. 将一副三角板如图放置,使两条直角边在一条直线上,其中 , .则 的度数是°.
 5. 如图,已知五边形 是正五边形,则 的度数是°.
5. 如图,已知五边形 是正五边形,则 的度数是°. 6. 如图,在正方形网格中,网格线的交点称为格点.已知A,B是两个格点,若点C也是图中的格点,且 为等腰三角形,则符合条件的点C有个.
6. 如图,在正方形网格中,网格线的交点称为格点.已知A,B是两个格点,若点C也是图中的格点,且 为等腰三角形,则符合条件的点C有个.
二、单选题
-
7. 2020年初,新冠病毒引发疫情.一方有难,八方支援.危难时刻,全国多家医院纷纷选派医护人员驰援武汉.下面是四家医院的图案标志,其中轴对称图形是( )A、
 B、
B、 C、
C、 D、
D、 8. 已知点 与点 关于x轴对称,则 的值为( )A、-1 B、0 C、1 D、29. 下列四个图形中,线段BE是△ABC的高的是( )A、
8. 已知点 与点 关于x轴对称,则 的值为( )A、-1 B、0 C、1 D、29. 下列四个图形中,线段BE是△ABC的高的是( )A、 B、
B、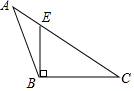 C、
C、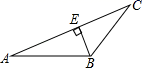 D、
D、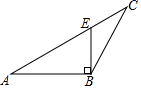 10. 若把分式 中的 和 同时扩大为原来的3倍,则分式的值( )A、扩大到原来的3倍 B、扩大到原来的6倍 C、缩小为原来的 D、不变11. 如图,在 中, ,线段 的垂直平分线交 于点 的周长是 ,则 的长为( )
10. 若把分式 中的 和 同时扩大为原来的3倍,则分式的值( )A、扩大到原来的3倍 B、扩大到原来的6倍 C、缩小为原来的 D、不变11. 如图,在 中, ,线段 的垂直平分线交 于点 的周长是 ,则 的长为( ) A、 B、 C、 D、12. 关于x的方程 的解为正数,则k的取值范围是( )A、 B、 C、 且 D、 且13. 为了疫情防控需要,某防护用品厂计划生产130000个口罩,但是在实际生产时,……,求实际每天生产口罩的个数,在这个题目中,若设实际每天生产口罩x个,可得方程 ,则题目中用“……”表示的条件应是( )A、每天比原计划多生产500个,结果延期10天完成 B、每天比原计划少生产500个,结果提前10天完成 C、每天比原计划少生产500个,结果延期10天完成 D、每天比原计划多生产500个,结果提前10天完成14. 如图,等腰直角 中, , 于点D, 的平分线分别交 、 于E、F两点,M为 的中点,延长 交 于点N,连接 .下列结论:① ;② ;③ ;④ .正确的有( )
A、 B、 C、 D、12. 关于x的方程 的解为正数,则k的取值范围是( )A、 B、 C、 且 D、 且13. 为了疫情防控需要,某防护用品厂计划生产130000个口罩,但是在实际生产时,……,求实际每天生产口罩的个数,在这个题目中,若设实际每天生产口罩x个,可得方程 ,则题目中用“……”表示的条件应是( )A、每天比原计划多生产500个,结果延期10天完成 B、每天比原计划少生产500个,结果提前10天完成 C、每天比原计划少生产500个,结果延期10天完成 D、每天比原计划多生产500个,结果提前10天完成14. 如图,等腰直角 中, , 于点D, 的平分线分别交 、 于E、F两点,M为 的中点,延长 交 于点N,连接 .下列结论:① ;② ;③ ;④ .正确的有( ) A、①② B、①②③ C、①②④ D、①②③④
A、①② B、①②③ C、①②④ D、①②③④三、解答题
-
15. 计算:(1)、 .(2)、 .16. 分解因式:(1)、 .(2)、 .17. 解方程: .18. 如图:已知 , 且 ,求证: .
 19. 先化简,再求值: ,其中 .20. 如图,在直角坐标系中, , , .
19. 先化简,再求值: ,其中 .20. 如图,在直角坐标系中, , , .
⑴在图中作出 关于y轴对称的图形 ,并写出点 的坐标.
⑵在y轴上找一点P,使 最小(不要求写做法,请保留作图痕迹).
21. 2020年底建成通车的保泸高速公路是进入云南省怒江州的第一条高速公路,它对完善云南高速公路网、巩固怒江州脱贫攻坚成果、带动滇西区域经济发展具有重大意义.保泸高速公路全长约85公里,比目前普通公路缩短了65公里,通行时间也比原来缩短了2个小时,若高速公路通行的平均速度是普通公路通行的平均速度的1.7倍,求保泸高速公路通车后的通行平均速度是多少?

