湖北省孝感市八校联谊2020-2021学年八年级上学期数学12月联考试卷
试卷更新日期:2021-10-13 类型:月考试卷
一、单选题
-
1. 下列四个图形中,是轴对称图形的为( )A、
 B、
B、 C、S
C、S  D、
D、 2. 下列式子中,正确的有( )
2. 下列式子中,正确的有( )①m3∙m5=m15; ②(a3)4=a7; ③(-a2)3=-(a3)2; ④(3x2)2=6x6
A、0个 B、1个 C、2个 D、3个3. 如图,在△ABC中,AB边上的高为( )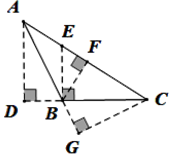 A、CG B、BF C、BE D、AD4. 若 中, ,且 ,那么 的度数为( )A、 B、 C、 D、5. 如图,从边长为 的正方形纸片中剪去一个边长为 的小正方形,剩余部分可剪拼成一个 不重叠、无缝隙的长方形,若拼成的长方形一边长为 ,则它另一边的长是( )
A、CG B、BF C、BE D、AD4. 若 中, ,且 ,那么 的度数为( )A、 B、 C、 D、5. 如图,从边长为 的正方形纸片中剪去一个边长为 的小正方形,剩余部分可剪拼成一个 不重叠、无缝隙的长方形,若拼成的长方形一边长为 ,则它另一边的长是( ) A、 B、 C、 D、6. 如图,在 中, ,线段 的垂直平分线交 于点 的周长是 ,则 的长为( )
A、 B、 C、 D、6. 如图,在 中, ,线段 的垂直平分线交 于点 的周长是 ,则 的长为( ) A、 B、 C、 D、7. 下列计算结果正确的是( )A、 B、 C、 ÷ D、8. 小明用长度分别为5,a,9的三根木棒首尾相接组成一个三角形,则a可能是( ).A、 B、 C、 D、9. 如图,下列说法中错误的是( )
A、 B、 C、 D、7. 下列计算结果正确的是( )A、 B、 C、 ÷ D、8. 小明用长度分别为5,a,9的三根木棒首尾相接组成一个三角形,则a可能是( ).A、 B、 C、 D、9. 如图,下列说法中错误的是( ) A、 不是三角形 的外角 B、 C、 是三角形 的外角 D、10. 如图,已知一个五边形 ABCDE纸片,一条直线将该纸片分割成两个多边形.若这两个多边形内角和分别为 m和 n,则 m+n不可能是( )
A、 不是三角形 的外角 B、 C、 是三角形 的外角 D、10. 如图,已知一个五边形 ABCDE纸片,一条直线将该纸片分割成两个多边形.若这两个多边形内角和分别为 m和 n,则 m+n不可能是( ) A、540° B、720° C、900° D、1080°
A、540° B、720° C、900° D、1080°二、填空题
-
11. 如图所示,则 .
 12. 当三角形的一个内角 是另一个内角 的3倍时,我们称此三角形为“特异三角形”,其中 称为“特异角”.若一个“特异三角形”为直角三角形,则这个“特异角”的度数为.13. 如图,点 在 内,且到三边的距离相等,若 ,则 的大小为.
12. 当三角形的一个内角 是另一个内角 的3倍时,我们称此三角形为“特异三角形”,其中 称为“特异角”.若一个“特异三角形”为直角三角形,则这个“特异角”的度数为.13. 如图,点 在 内,且到三边的距离相等,若 ,则 的大小为. 14. 嘉嘉和淇淇下棋,嘉嘉执圆形棋子,淇淇执方形棋子,如图,棋盘中心的圆形棋子的位置用 表示,右下角的圆形棋子用 表示,淇淇将第 枚方形棋子放入棋盘后,所有棋子构成的图形是轴对称图形.则淇淇放的方形棋子的位置是.
14. 嘉嘉和淇淇下棋,嘉嘉执圆形棋子,淇淇执方形棋子,如图,棋盘中心的圆形棋子的位置用 表示,右下角的圆形棋子用 表示,淇淇将第 枚方形棋子放入棋盘后,所有棋子构成的图形是轴对称图形.则淇淇放的方形棋子的位置是. 15. 如图,线段 的垂直平分线 交于点 .若 ,则
15. 如图,线段 的垂直平分线 交于点 .若 ,则 16. 在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,PR=PS,AQ=PQ,则下面三个结论:①AS=AR;②PQ∥AR;③△BRP≌△CSP.其中正确的是.
16. 在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,PR=PS,AQ=PQ,则下面三个结论:①AS=AR;②PQ∥AR;③△BRP≌△CSP.其中正确的是.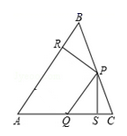
三、解答题
-
17.(1)、(2)、18. 用简便方法计算:(1)、(2)、19. 如图, 在同一条直线上 交 于点 ,且 .求证:
 (1)、(2)、20. 如图,在 的正方形网格中,每个小正方形的边长都为 ,网格中有一个格点 (即三角形的顶点都在格点上).
(1)、(2)、20. 如图,在 的正方形网格中,每个小正方形的边长都为 ,网格中有一个格点 (即三角形的顶点都在格点上). (1)、在图中作出 关于直线 对称的 ;(要求: 与 与 与 相对应)(2)、若有一格点 到点的 距离相等( ), 则网格中满足条件的点 共有个;(3)、在直线 上找一点 ,使 的值最小.21. 我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了 (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应 展开式中的系数;第四行的四个数1,3,3,1,恰好对应着 展开式中的系数等等.
(1)、在图中作出 关于直线 对称的 ;(要求: 与 与 与 相对应)(2)、若有一格点 到点的 距离相等( ), 则网格中满足条件的点 共有个;(3)、在直线 上找一点 ,使 的值最小.21. 我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了 (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应 展开式中的系数;第四行的四个数1,3,3,1,恰好对应着 展开式中的系数等等. (1)、根据上面的规律,写出 的展开式.(2)、利用上面的规律计算:22. 如图,点 、 、 在一条直线上, , , ;
(1)、根据上面的规律,写出 的展开式.(2)、利用上面的规律计算:22. 如图,点 、 、 在一条直线上, , , ;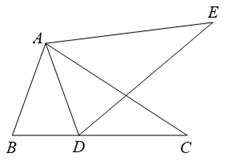 (1)、求证: ;(2)、若 ,求 .23. 对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到 ,请解答下列问题
(1)、求证: ;(2)、若 ,求 .23. 对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到 ,请解答下列问题 (1)、写出图2中所表示的数学等式
(1)、写出图2中所表示的数学等式 (2)、根据整式乘法的运算法则,通过计算验证上述等式;(3)、利用(1)中得到的结论,解决下面的问题:若 ,则(4)、小明同学用图3中 张边长为 的正方形, 张边长为 的正方形 张边长分别为 的长方形纸片拼出一个面积为 长方形,则
(2)、根据整式乘法的运算法则,通过计算验证上述等式;(3)、利用(1)中得到的结论,解决下面的问题:若 ,则(4)、小明同学用图3中 张边长为 的正方形, 张边长为 的正方形 张边长分别为 的长方形纸片拼出一个面积为 长方形,则 24. 在平面直角坐标系中,点 , ,点C为x轴正半轴上一动点,过点A作 交y轴于点E.
24. 在平面直角坐标系中,点 , ,点C为x轴正半轴上一动点,过点A作 交y轴于点E.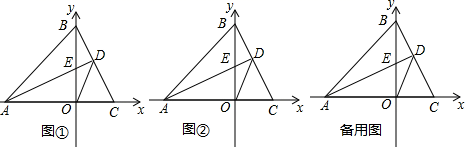 (1)、如图 ,若点C的坐标为 ,试求点E的坐标;(2)、如图 ,若点C在x轴正半轴上运动,且 , 其它条件不变,连接DO,求证:OD平分(3)、若点C在x轴正半轴上运动,当 时,求 的度数.
(1)、如图 ,若点C的坐标为 ,试求点E的坐标;(2)、如图 ,若点C在x轴正半轴上运动,且 , 其它条件不变,连接DO,求证:OD平分(3)、若点C在x轴正半轴上运动,当 时,求 的度数.