云南省红河哈尼族彝族自治州石屏县2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-10-13 类型:期末考试
一、填空题
-
1. 计算 .2. 据某媒体报道,今年“国庆”黄金周期间,我省旅游收入再创历史新高,达 元,用科学记数法表示为元.3. 单项式 与 是同类项,则 , .4. 一次函数的图象经过(-1,0)且函数值随自变量增大而减小,写出一个符合条件的一次函数解析式 .5. 因式分解: .6. 如图,点B在AE上,∠CAB=∠DAB , 要使 ,可补充的一个条件是: .
 7. 已知m是整数,且一次函数 的图象不经过第二象限,则 .8. 某灯泡厂一次质量检查中,从300个灯泡中抽查了50个,其中有3个不合格,则出现不合格灯泡的频率是 , 在这300个灯泡中估计有个为不合格产品.9. 已知直线yy′⊥xx′,垂足为O,则图形①与图形成轴对称
7. 已知m是整数,且一次函数 的图象不经过第二象限,则 .8. 某灯泡厂一次质量检查中,从300个灯泡中抽查了50个,其中有3个不合格,则出现不合格灯泡的频率是 , 在这300个灯泡中估计有个为不合格产品.9. 已知直线yy′⊥xx′,垂足为O,则图形①与图形成轴对称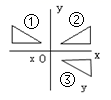 10. 若直线 和直线 的交点坐标为 .则 , .
10. 若直线 和直线 的交点坐标为 .则 , .二、单选题
-
11. 我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式,例如图甲可以用来解释 .那么通过图乙面积的计算,验证了一个恒等式,此等式是( )
 A、 B、 C、 D、12. 正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )A、
A、 B、 C、 D、12. 正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )A、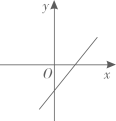 B、
B、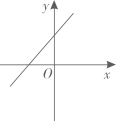 C、
C、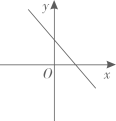 D、
D、 13. 能清楚地看出各部分与总数之间的百分比关系的是( )A、条形统计图 B、扇形统计图 C、折线统计图 D、以上均可以14. 观察由等腰梯形组成的下图和所给表中数据的规律后回答问题:
13. 能清楚地看出各部分与总数之间的百分比关系的是( )A、条形统计图 B、扇形统计图 C、折线统计图 D、以上均可以14. 观察由等腰梯形组成的下图和所给表中数据的规律后回答问题:
梯形个数
....
图形周长
.....
当等腰梯形个数为2006时,图形的周长为( )
A、 B、 C、 D、15. 下列说法正确的是:( )A、等腰三角形的高、中线、角平分线互相重合 B、顶角相等的两个等腰三角形全等 C、等腰三角形一边不可以是另一边的二倍 D、等腰三角形的两个底角相等16. 夏天,一杯开水放在桌子上,杯中水的温度 随时间t变化的关系的大致图象是( )A、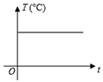 B、
B、 C、
C、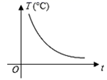 D、
D、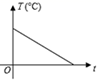 17. 如图,点P到 、 、 的距离恰好相等,则点P的位置:①在 的平分线上;②在 的平分线上;③在 的平分线上;④恰好是 、 、 三条平分线的交点.上述结论中,正确的个数有( )
17. 如图,点P到 、 、 的距离恰好相等,则点P的位置:①在 的平分线上;②在 的平分线上;③在 的平分线上;④恰好是 、 、 三条平分线的交点.上述结论中,正确的个数有( )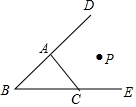 A、 个 B、 个 C、 个 D、 个18. 下列图案中是轴对称图形的有 ( )
A、 个 B、 个 C、 个 D、 个18. 下列图案中是轴对称图形的有 ( ) A、1个 B、2个 C、3个 D、4个19. 如图, 是 中 边的垂直平分线,若 厘米, 厘米,则 的周长为( )
A、1个 B、2个 C、3个 D、4个19. 如图, 是 中 边的垂直平分线,若 厘米, 厘米,则 的周长为( )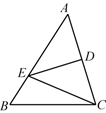 A、16 B、18 C、26 D、2820. 某弹簧的长度y与所挂物体的质量x(kg)之间的关系为一次函数,其函数图象如图所示,则不挂物体时弹簧的长度为( )
A、16 B、18 C、26 D、2820. 某弹簧的长度y与所挂物体的质量x(kg)之间的关系为一次函数,其函数图象如图所示,则不挂物体时弹簧的长度为( ) A、 B、 C、 D、
A、 B、 C、 D、三、解答题
-
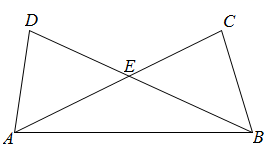
21. 先化简求值: ,其中 , .22. 如图:给出五个等量关系:① ,② ,③ ,④ ,⑤ .请你以其中两个为条件,另三个中的一个为结论,写出三个正确的结论,并任选其中一个加以证明.
 23. 某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若某户居民应交交费y(元)与用水量x(吨)的函数关系如图所示.
23. 某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若某户居民应交交费y(元)与用水量x(吨)的函数关系如图所示. (1)、分别写出当 和 时,y与x的函数关系式;(2)、若某用户该月用水21吨,则应交水费多少元?24. 如图,准备在一条公路旁修建一个仓储基地,分别给A、B两个超市配货,那么这个基地建在什么位置,能使它到两个超市的距离之和最小?(保留作图痕迹及简要说明)
(1)、分别写出当 和 时,y与x的函数关系式;(2)、若某用户该月用水21吨,则应交水费多少元?24. 如图,准备在一条公路旁修建一个仓储基地,分别给A、B两个超市配货,那么这个基地建在什么位置,能使它到两个超市的距离之和最小?(保留作图痕迹及简要说明) 25. 小明到6千米远的西湖去玩,请根据右面折线统计图回答:
25. 小明到6千米远的西湖去玩,请根据右面折线统计图回答: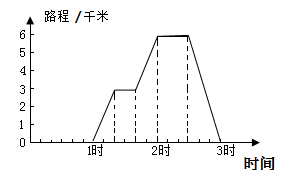 (1)、小明在西湖玩了多少时间?(2)、如果从出发起一直走不休息,几点几分可以到达西湖?(3)、求出返回时小明骑自行车的速度.26. 学了《数据的收集与表示》后,小刚就本班同学的上学方式进行了一次调查统计,左图和右图是他通过采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
(1)、小明在西湖玩了多少时间?(2)、如果从出发起一直走不休息,几点几分可以到达西湖?(3)、求出返回时小明骑自行车的速度.26. 学了《数据的收集与表示》后,小刚就本班同学的上学方式进行了一次调查统计,左图和右图是他通过采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题: (1)、求该班共有多少名学生?(2)、在图中,将表示“步行”的部分补充完整;(3)、在扇形统计图中,计算出“骑车”部分所对应的圆心角的度数;(4)、如果全年级共500名同学,请你估算全年级步行上学的学生人数.
(1)、求该班共有多少名学生?(2)、在图中,将表示“步行”的部分补充完整;(3)、在扇形统计图中,计算出“骑车”部分所对应的圆心角的度数;(4)、如果全年级共500名同学,请你估算全年级步行上学的学生人数.