山西省吕梁市孝义市2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-10-13 类型：期末考试

进入出卷网下载

一、单选题

1. 下列长度的三条线段能组成三角形的是（）

A、1，2，3 B、1，2，2， C、3，3，6.5 D、4，4，9

查看试题解析
2. 下列交通标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 将一副三角板按图中方式叠放，则∠ $α$ 的度数为（）

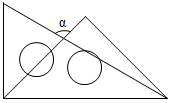A、85° B、95° C、105° D、115°

查看试题解析
4. 点A（2，-3）关于x轴对称的点的坐标是（）

A、（-2，-3） B、（-2，3） C、（2，3） D、（2，-3）

查看试题解析
5. 新型冠状病毒，有包膜，颗粒呈圆形或者椭圆形，常为多形性，直径约60-140纳米.140纳米用科学记数法表示为（1纳米=10^-9米）（）

A、1.40×10^-11 B、1.40×10^-10 C、1.40×10^-8 D、1.40×10^-7

查看试题解析
6. 下列运算错误的是（）

A、 $x^{3} \cdot x^{5} = x^{8}$ B、 $x^{5} \div x = x^{4}$ C、 ${(x^{3})}^{3} = x^{9}$ D、 ${(x^{2} y)}^{3} = x^{2} y^{3}$

查看试题解析
7. 下列分解因式正确的是（）

A、 $a^{3} - a = a (a^{2} - 1)$ B、 $x^{3} + 4 x^{2} y + 4 x y^{2}$ = $x {(x + 2 y)}^{2}$ C、 $- x^{2} + 4 x y - 4 y^{2} = - {(x + 2 y)}^{2}$ D、 $16 x^{2} + 16 x + 4 = {(4 x + 2)}^{2}$

查看试题解析
8. 数学课上，探究角的平分线的作法时，小宇用直尺和圆规作∠AOB的平分线，方法如下：
如图，⑴以点O为圆心，适当长为半径画弧，交OA 于点M ，交OB 于点N；

⑵分别以点M ， N为圆心，大于 $\frac{1}{2}$ MN 的长为半径画弧，两弧在∠AOB的内部相交于点C；

⑶画射线OC ．射线OC即为所求．其中的道理是，作出△OMC≌△ONC ，根据全等三角形的性质，得到∠AOC=∠BOC ，进而得到OC是∠AOB的平分线．其中，△OMC≌△ONC的依据是（）

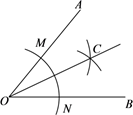A、SSS B、SAS C、ASA D、AAS

查看试题解析
9. 解分式方程 $\frac{1 - x}{x - 3} = \frac{1}{3 - x} - 3$ 时，去分母变形正确的是（）

A、 $1 - x = 1 - 3 (x - 3)$ B、 $- 1 + x = 1 + 3 (3 - x)$ C、 $1 - x = - 1 - 3 (x - 3)$ D、 $- 1 + x = 1 - 3 (x - 3)$

查看试题解析
10. 如图，△ABC和△ADE中，AB=AC ， AD=AE ， ∠BAC=∠DAE ，且点B ， D ， E在同一条直线上，若∠CAE+∠ACE+∠ADE=130°，则∠ADE的度数为（）

A、50° B、65° C、70° D、75°

查看试题解析

二、填空题

11. 下图是跪姿射击的情形．我们可以看到，跪姿射击的动作构成了三个三角形∶一是由右脚尖、右膝、左脚构成的三角形支撑面；二是由左手、左肘、左肩构成的托枪三角形；三是由左手、左肩、右肩所构成的近乎水平的三角形．这三个三角形可以使射击者在射击过程中保持稳定．其中，蕴含的数学道理是．

查看试题解析
12. 如图，在三角形ABC中，∠C＝90°，BD平分∠ABC交AC于点D ，且AD＝2CD ， AC＝6，点E是AB上一点，连接DE ，则DE的最小值为．

查看试题解析
13. 乐乐家离姥姥家20km，乐乐坐公交从家到姥姥家，需要xh，骑自行车从家到姥姥家所用的时间比坐公交所用的时间多1h．则骑自行车的平均速度为km/h（用含x式子表示）．

查看试题解析
14. 边长相等的正方边形ABFG和正五边形BCDEF如图所示拼接在一起，则∠FGE=°．

查看试题解析
15. 如图，线段AB=10，点C是线段AB上一点（点C不与点A ， B重合），分别以AC ， BC为边作正方形ACDE和BCGF ，连接AG ，记正方形ACDE ， BCGF的面积分别为S₁ ， S₂ ， △ACG的面积为S₃ ，若S₁+S₂=58，则S₃的值为．

查看试题解析

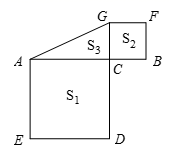
三、解答题

16.

(1)、计算： ${(- \frac{1}{2})}^{- 3} + {(- 3)}^{2} - {(- \frac{1}{4})}^{0}$

(2)、化简： $(\frac{1}{x + 1} - 1) \div \frac{x}{x^{2} - 1}$

(3)、先化简，再求值： ${(2 a + 3 b)}^{2} - (2 a + b) (2 a - b)$ ，其中 $a = \frac{1}{3}$ ， $b = - \frac{1}{2}$ ．

查看试题解析
17. 解方程： $\frac{x}{x - 1} = \frac{3}{2 x - 2} - 2$

查看试题解析
18. 如图，AD ， AF分别是△ABC的高和角平分线，已知∠B=65°，∠C=35°，求∠DAF的度数．

查看试题解析
19.

(1)、如图，已知线段m，n．求作△ABC ，请在右面的空白处作△ABC ，作∠ACB=90°，AC=m，AB=n（尺规作图，不写作法，保留作图痕迹）．

(2)、婷婷将（1）中自己画的△ABC剪下来，放在同桌悦悦所画的△ABC上，发现两三角形完全重合，这一过程验证了三角形全等的哪一种判定定理：（直接写出答案，不写过程）．

查看试题解析
20. 今年11月14日，“行孝仗义，柿柿如意”2020第三届孝义柿子文化节在兑镇镇产树原村隆重开幕．柿子是孝义市地理标志农产品，开发柿子产业是转型跨越发展致富的新路．某食品公司有一批新鲜柿子，公司将一部分新鲜柿子直接销售，这批新鲜柿子的总售价为4000元，剩余的一部分加工成柿饼后进行销售，这批柿饼的总售价为80000元．已知柿饼的销售数量比直接销售的新鲜柿子多2000千克，且每千克的售价是新鲜柿子的10倍．求新鲜柿子和柿饼每千克的售价各多少元？

查看试题解析
21. 阅读下列材料，完成相应任务．
三角形中边与角之间的不等关系

学习了等腰三角形，我们知道：在一个三角形中，等边所对的角相等；反过来，等角所对的边也相等．那么，不相等的边所对的角之间的大小关系怎样呢？大边所对的角也大吗？下面是奋进小组的证明过程．

如图1，在△ABC中，已知AB＞AC＞BC ．

求证：∠C＞∠B＞∠A ．

证明：如图2，将△ABC折叠，使边AC落在AB上，

点C落在AB上的点C′处，折痕AD交BC于点D ．

则∠A C′D=∠C ．

∵∠A C′D=∠B+∠BDC′（依据1）

∴∠A C′D＞∠B

∴∠C＞∠B（依据2）

如图3，将△ABC折叠，使边CB落在CA上，点B落在CA上的点B′处，折痕CE交AB于点E ．则∠CB′E=∠B ．

∵∠CB′E=∠A+∠AEB′

∴∠CB′E＞∠A

∴∠B＞∠A

∴∠C＞∠B＞∠A ．

归纳总结：利用轴对称的性质可以把研究边与角之间的不等问题，转化为较大量的一部分与较小量相等的问题，这是几何中研究不等问题是常用的方法．

类似地，应用这种方法可以证明“在一个三角形中，大角对大边，小角对小边”的问题．如图1，已知△ABC中，∠C＞∠B＞∠A ．求证：AB＞AC＞BC ．下面是智慧小组的证明过程（不完整）．

证明：如图2，在∠BCA的内部，作∠BCF=∠B ， CF交AB于点F ．

则CF=BF（依据3）

在△ACF中，AF+CF＞AC ，

∴AF+BF＞AC ，

∴AB＞AC；…

(1)、任务一：
①上述材料中依据1，依据2，依据3分别指什么？

依据1：；

依据2：；

依据3：．

A．转化思想 B．方程思想 C．数形结合思想

(2)、②上述材料中不论是由边的不等关系，推出角的不等关系，还是由角的不等关系推出边的不等关系，都是转化为较大量的一部分与较小量相等的问题，再用三角形外角的性质或三边关系进而解决，这里主要体现的数学思想是；（填符合题意选项的代码）

(3)、任务二：请将智慧小组的证明过程补充完整，并在备用图中作出辅助线．

(4)、任务三：根据上述材料得出的结论，判断下列说法，正确的有（将正确的代码填在横线处）．
①在△ABC中，AB＞BC ，则∠A＞∠B；

②在△ABC中，AB＞BC＞AC ， ∠C=89°，则△ABC是锐角三角形；

③Rt△ABC中，∠B=90°，则最长边是AC；

④在△ABC中，∠A=55°，∠B=70°，则AB=BC ．

查看试题解析
22. 实践与探究
如图1，三角尺ABC和三角尺DEF是两个全等的直角三角尺，其中，∠A=∠D=60°，∠B=∠E=30°，∠C=∠F=90°．

(1)、操作发现
如图2，将三角尺ABC和三角尺DEF如图摆放，连接CF ，交AB于点G ，请你证明CG= FG；

(2)、在图2的基础上，将三角尺DEF沿BA方向平移至图3的位置，兴趣小组发现CG仍然与FG相等，请你证明CG= FG；

(3)、在图3的基础上，将三角尺DEF沿BA方向继续平移，使CF经过点A ，如图4所示，兴趣小组测得BD=20.4cm，则三角尺DEF由图2所示位置平移至图4 的位置，平移的距离为cm（直接写出答案，不写过程）．

查看试题解析