湖北省通山县沙店中学2020-2021学年八年级上学期数学12月月考试卷

试卷更新日期：2021-10-13 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列“慢行通过，注意危险，禁止行人通行，禁止非机动车通行”四个交通标志图（黑白阴影图片）中为轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC于点D，CD=2，则点D到AB的距离是（）

A、1 B、2 C、3 D、4

查看试题解析
3. 如图，△ABD≌△EBC，且AB=3，BC=5，则DE的长为（）

A、5 B、4 C、3 D、2

查看试题解析
4.
如图，在下列条件中，不能证明△ABD≌△ACD的是（）.

A、BD=DC ， AB=AC B、∠ADB=∠ADC ， BD=DC C、∠B=∠C ， ∠BAD=∠CAD D、∠B=∠C ， BD=DC

查看试题解析
5. 如图，在△ABC中，点D，E，F分别是BC，AD，EC的中点，若△ABC的面积是16.则△BEF的面积为（）

A、4 B、6 C、8 D、10

查看试题解析
6. 如图，在△PAB中，PA=PB，D、E、F分别是边PA、PB、AB上的点，且AD=BF，BE=AF.若∠DFE=34°，则∠P的度数为（）

A、150° B、112° C、120° D、146°

查看试题解析
7. 如图，在Rt△ABC中，∠A＝30°，DE垂直平分AB，垂足为点E，交AC于D点，连接BD，若DE＝2，则AC的值为（）

A、4 B、6 C、8 D、10

查看试题解析
8. 如图，△ $A B C$ 中， $∠ A B C$ 、 $∠ E A C$ 的角平分线 $B P$ 、 $A P$ 交于点 $P$ ，延长 $B A$ 、 $B C$ ， $P M ⊥ B E$ ， $P N ⊥ B C$ ，则下列结论中正确的个数是（）
①CP平分∠ACF；②∠ABC+2∠APC=180°；③∠ACB=2∠APB④若PM⊥BE，PN⊥BC，则AM+CN=AC；

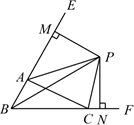A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 等腰三角形的对称轴是.

查看试题解析
10. 已知A（3， $y$ ）、B（ $x$ ，5）关于 $y$ 轴对称，由 $x + y$ =.

查看试题解析
11. 如图，在三角形纸片中， $A B = 8 c m ， B C = 5 c m ， A C = 6 c m$ ，沿过点 $B$ 的直线折叠这个三角形，使点 $C$ 落在 $A B$ 边上的点 $E$ 处，折痕为 $B D$ ，则 $Δ A E D$ 的周长等于 $c m$ .

查看试题解析
12. 如图，在△ABC中，AB＝AC，∠A＝40°，AB的垂直平分线MN交AC于点D，则∠DBC＝度.

查看试题解析
13. Rt△ABC中，∠C=90°，AD平分∠BAC交BC于D，CD=8，P为AB上任一点，则DP的最小值为.

查看试题解析
14. 已知等腰三角形一腰上的高与另一腰的夹角为40度，则等腰三角形的底角是.

查看试题解析
15. 如图，在Rt△ABC中，∠ACB=90°，EF垂直平分AB，AC=3，BC=4，则AE+CE的最小值是.

查看试题解析
16. 如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于D，下列四个结论：

①EF=BE+CF；

②∠BOC=90°+ $\frac{1}{2}$ ∠A；

③点O到△ABC各边的距离相等；

④设OD=m，AE+AF=n，则 $S_{Δ A E F} = m n$ .

其中正确的结论是.（填序号）

查看试题解析

三、解答题

17. 已知|a－b－1|＋（b－2）²＝0，求边长为a，b的等腰三角形的周长.

查看试题解析
18. 如图所示，D为△ABC的边AB的延长线上一点，过D作DF⊥AC，垂足为F，交BC于E，且BD＝BE，求证△ABC是等腰三角形.

查看试题解析
19. 如图，ABC在正方形网格中，A（4，2）、B（-1，1）、C（1，4）.作出△ABC关于 $x$ 轴对称的对称图形△A’B’C’（不写作法），并求△A’B’C’的面积.

查看试题解析
20. 如图，在△ABC中，AB=AC，AE⊥BE于点E，且BE= $\frac{1}{2}$ BC.

(1)、求证：BA平分∠EBC；

(2)、若∠ABE=70°，求∠EAC的度数.

查看试题解析
21. 如图，在△ABC中，∠C=2∠B，AD是△ABC的角平分线，∠1=∠B.
求证：AB=AC+CD.

查看试题解析
22. 如图，∠BAD=∠CAE=90°，AB=AD，AE=AC.

(1)、若AC=20，求四边形ABCD的面积；

(2)、求证：AC平分∠BCE.

查看试题解析
23. 如图

问题情境：如图①，在△ABD与△CAE中，BD=AE，∠DBA=∠EAC，AB=AC，易证：△ABD≌△CAE.（不需要证明）

(1)、特例探究：如图②，在等边△ABC中，点D、E分别在边BC、AB上，且BD=AE，AD与CE交于点F.求证：△ABD≌△CAE.

(2)、归纳证明：如图③，在等边△ABC中，点D、E分别在边CB、BA的延长线上，且BD=AE.△ABD与△CAE是否全等？如果全等，请证明；如果不全等，请说明理由.

(3)、拓展应用：如图④，在等腰三角形中，AB=AC，点O是AB边的垂直平分线与AC的交点，点D、E分别在OB、BA的延长线上.若BD=AE，∠BAC=50°，∠AEC=32°，求∠BAD的度数.

查看试题解析
24. 已知：如图，△ABC是边长为6 cm的等边三角形，动点P，Q同时从A，B两点出发，分别在AB，BC边上匀速移动，它们的速度分别是V_p＝2 cm/s，V_Q＝1 cm/s.当点P到达点B时，P，Q两点同时停止运动，设点P运动的时间为t s.

(1)、当t为何值时，△PBQ为等边三角形？

(2)、当t为何值时，△PBQ为直角三角形？

查看试题解析