山西省临汾市翼城县2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-10-13 类型:期末考试
一、单选题
-
1. 下列各数中,属于无理数的是( )A、 B、1.414 C、 D、2. “ 的算术平方根是 ”用数学式子表示正确的是( )A、 B、 C、 D、3. 如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么,最省事的方法是( )
 A、带①去 B、带②去 C、带③去 D、带①去和带②去4. 下列运算正确的是( )A、 B、 C、 D、5. 下列四组线段中,可以构成直角三角形的是( )A、 B、 C、 D、6. 用反证法证明:在 中, 中不能有两个角是钝角时,假设 中有两个角是钝角,令 ,则所得结论与下列四个选项相矛盾的是( )A、已知 B、三角形内角和等于 C、钝角三角形的定义 D、以上结论都不对7. 已知△ABC , 两个完全一样的三角板如图摆放,它们的一组对应直角边分别在AB , AC上,且这组对应边所对的顶点重合于点M , 点M一定在( )
A、带①去 B、带②去 C、带③去 D、带①去和带②去4. 下列运算正确的是( )A、 B、 C、 D、5. 下列四组线段中,可以构成直角三角形的是( )A、 B、 C、 D、6. 用反证法证明:在 中, 中不能有两个角是钝角时,假设 中有两个角是钝角,令 ,则所得结论与下列四个选项相矛盾的是( )A、已知 B、三角形内角和等于 C、钝角三角形的定义 D、以上结论都不对7. 已知△ABC , 两个完全一样的三角板如图摆放,它们的一组对应直角边分别在AB , AC上,且这组对应边所对的顶点重合于点M , 点M一定在( )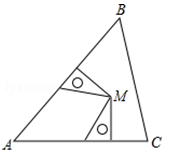 A、∠A的平分线上 B、AC边的高上 C、BC边的垂直平分线上 D、AB边的中线上8. 如果两数和的平方的结果是 ,那么a的值是( )A、 B、 或 C、 或 D、9. 如图,图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若 ,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
A、∠A的平分线上 B、AC边的高上 C、BC边的垂直平分线上 D、AB边的中线上8. 如果两数和的平方的结果是 ,那么a的值是( )A、 B、 或 C、 或 D、9. 如图,图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若 ,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )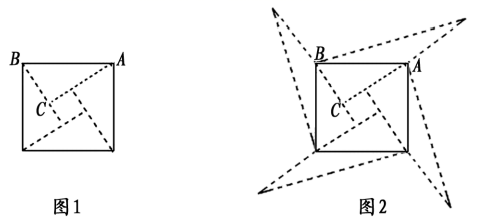 A、 B、 C、 D、10. 如图,在 中, ,以点C为圆心, 长为半径 画弧,交 于点B和点D,再分别以点 为圆心,大于 长为半径画弧,两弧相交于点M,作射线 交 于点E.若 ,则 的长度是( )
A、 B、 C、 D、10. 如图,在 中, ,以点C为圆心, 长为半径 画弧,交 于点B和点D,再分别以点 为圆心,大于 长为半径画弧,两弧相交于点M,作射线 交 于点E.若 ,则 的长度是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算: .12. 如图, 和 中, ,在不添加任何辅助线和字母的情况下,请你添加一个条件使 和 全等.
 13. 写出一个比 大且比 小的整数 .14. 下列命题,①对顶角相等;②两直线平行,同位角相等;③全等三角形的对应角相等.其中逆命题是真命题的命题共有个.15. 如图,在 中, 是 边上的中线, ,则
13. 写出一个比 大且比 小的整数 .14. 下列命题,①对顶角相等;②两直线平行,同位角相等;③全等三角形的对应角相等.其中逆命题是真命题的命题共有个.15. 如图,在 中, 是 边上的中线, ,则 16. 已知 ,点C为射线 上一点,点D为 的中点,且 .当点P在射线 上运动时 ,则 与 和的最小值为 .
16. 已知 ,点C为射线 上一点,点D为 的中点,且 .当点P在射线 上运动时 ,则 与 和的最小值为 .
三、解答题
-
17. 计算(1)、(2)、 ;(3)、先化简﹐再求值: ,其中18. 因式分解:(1)、(2)、 .19.(1)、根据(1)作出的图形说明 的理由﹔(2)、根据 ,请用一句话归纳出一个结论.(3)、如图,已知 ,用直尺和圆规作 ,使得 , , ,并在 和 中﹐作出 的平分线 和 的平分线 (不写作法﹐保留作图痕迹);
 20. 如图,在 中, , , 垂直平分 ,交 于点E;D为垂足,连接
20. 如图,在 中, , , 垂直平分 ,交 于点E;D为垂足,连接 (1)、求 的度数;(2)、若 ,求 的长.21. 为迎接2020年第 届全国青少年科技创新大赛,某学校举办了 机器人; 航模; 科幻绘画; 信息学; 科技小制作等五项比赛活动(每人限报一项),将各项比赛的参加人数绘制成如图两幅不完整的统计图.
(1)、求 的度数;(2)、若 ,求 的长.21. 为迎接2020年第 届全国青少年科技创新大赛,某学校举办了 机器人; 航模; 科幻绘画; 信息学; 科技小制作等五项比赛活动(每人限报一项),将各项比赛的参加人数绘制成如图两幅不完整的统计图.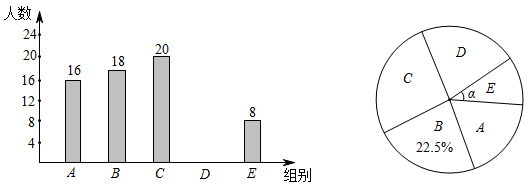
根据统计图中的信息解答下列问题:
(1)、本次参加比赛的学生人数是 名;(2)、把条形统计图补充完整;(3)、求扇形统计图中表示科技小制作的扇形圆心角的度数.22. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙脚的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,求小巷的宽度.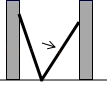 23. 如图(1),大正方形的面积可以表示为 ,同时大正方形的面积也可以表示成两个小正方形面积与两个长方形的面积之和,即 .同一图形(大正方形)的面积,用两种不同的方法求得的结果应该相等,从而验证了完全平方公式: .把这种“同一图形的面积,用两种不同的方法求出的结果相等,从而构建等式,根据等式解决相关问题”的方法称为“面积法”
23. 如图(1),大正方形的面积可以表示为 ,同时大正方形的面积也可以表示成两个小正方形面积与两个长方形的面积之和,即 .同一图形(大正方形)的面积,用两种不同的方法求得的结果应该相等,从而验证了完全平方公式: .把这种“同一图形的面积,用两种不同的方法求出的结果相等,从而构建等式,根据等式解决相关问题”的方法称为“面积法” (1)、用上述“面积法”,通过如图(2)中图形的面积关系,直接写出一个多项式进行因式分解的等式:;
(1)、用上述“面积法”,通过如图(2)中图形的面积关系,直接写出一个多项式进行因式分解的等式:; (2)、如图(3), 中, , , , 是斜边 边上的高.用上述“面积法”求 的长;
(2)、如图(3), 中, , , , 是斜边 边上的高.用上述“面积法”求 的长; (3)、如图(4),等腰 中, ,点O为底边 上任意一点, , , ,垂足分别为点M,N,H,连接 ,用上述“面积法”,求证: .
(3)、如图(4),等腰 中, ,点O为底边 上任意一点, , , ,垂足分别为点M,N,H,连接 ,用上述“面积法”,求证: . 24. 如图,在 中, ,点 为直线 上一动点,连接 ,以 为直角边作等腰直角三角形 .
24. 如图,在 中, ,点 为直线 上一动点,连接 ,以 为直角边作等腰直角三角形 .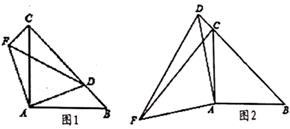 (1)、如图1,若当点 在线段 上时(不与点 重合),证明: ;(2)、如图2,当点 在线段 的延长线上时,试猜想 与 的数量关系和位置关系,并说明理由.
(1)、如图1,若当点 在线段 上时(不与点 重合),证明: ;(2)、如图2,当点 在线段 的延长线上时,试猜想 与 的数量关系和位置关系,并说明理由.