山西省临汾市襄汾县2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-10-13 类型：期末考试

进入出卷网下载

一、单选题

1. ${(- 2)}^{2}$ 的算术平方根是（）

A、2 B、 $- 2$ C、 $\pm 2$ D、 $\sqrt{2}$

查看试题解析
2. 下列运算正确的是（）

A、 $a^{3} \cdot a^{4} = a^{12}$ B、 ${(- a^{4})}^{3} = a^{12}$ C、 ${(2 y^{2})}^{3} = 6 y^{6}$ D、 $a^{12} \div a^{2} = a^{10}$

查看试题解析
3. 如图，乐乐书上的三角形墨迹污染了一部分，很快他就画出一个三角形与书上的三角形全等，这两个三角形全等的依据是（）

A、 $S S S$ B、 $A S A$ C、 $A A S$ D、 $S A S$

查看试题解析
4. 能够直观、形象地显示各个量在总量中所占份额的是（）

A、扇形统计图 B、条形统计图 C、折线统计图 D、频数分布直方图

查看试题解析
5. 以下列线段a、b、c的长为边，不能构成直角三角形的是（）．

A、 $a = 8$ ， $b = 10$ ， $c = 12$ B、 $a = 1$ ， $b = 2$ ， $c = \sqrt{3}$ C、 $a = 25$ ， $b = 20$ ， $c = 15$ D、 $a ： b ： c = 5 ： 12 ： 13$

查看试题解析
6. 牛顿曾说过：“反证法是数学家最精良的武器之一．”那么我们用反证法证明：“在一个三角形中，至少有一个内角小于或等于60°”时，第一步先假设（）

A、三角形中有一个内角小于60° B、三角形中有一个内角大于60° C、三角形中每个内角都大于60° D、三角形中没有一个内角小于60°

查看试题解析
7. 下列命题的逆命题是真命题的是（）．

A、 $\sqrt{3}$ 的平方根是3 B、 $\sqrt{5}$ 是无理数 C、1的立方根是1 D、全等三角形的周长相等

查看试题解析
8. 我们利用尺规作图可以作一个角 $(∠ A' O' B)$ 等于已知角 $(∠ A O B)$ ，如下所示：

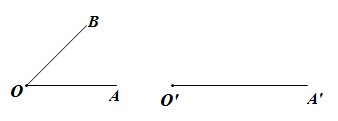
⑴作射线 $O A$ ；

⑵以O为圆心，任意长为半径作弧，交 $O A$ 于C，交 $O B$ 于D；

⑶以 $O^{'}$ 为圆心， $O C$ 为半径作弧，交 $O A^{'}$ 于 $C'$ ；

⑷以 $C^{'}$ 为圆心， $O C$ 为半径作弧，交前面的弧于 $D^{'}$ ；

⑸连接 $O^{'} D'$ 作射线 $O^{'} B^{'} ，$ 则 $∠ A^{'} O^{'} B^{'}$ 就是所求作的角．

以上作法中，错误的一步是（）

A、 $(2)$ B、 $(3)$ C、 $(4)$ D、 $(5)$

查看试题解析
9. 已知 $R t △ A B C$ 中， $∠ A$ ， $∠ B$ ， $∠ C$ 的对边分别为a、b、c，若 $∠ B = 90 °$ ，则（）．

A、 $b^{2} = a^{2} + c^{2}$ B、 $c^{2} = a^{2} + b^{2}$ C、 $a^{2} = c^{2} + b^{2}$ D、 $a + b = c$

查看试题解析
10. 如图所示，已知 $△ A B C$ 和 $△ D C E$ 均是等边三角形，点B、C、E在同一条直线上，连接 $A E$ 、 $B D$ 、 $F G$ ， $A E$ 与 $B D$ 交于点O， $A E$ 与 $C D$ 交于点G， $A C$ 与 $B D$ 交于点F，则下列结论中：
① $A E = B D$ ； ② $A G = B F$ ； ③ $F G // B E$ ； ④ $C F = C G$ ，以上结论正确的有（）

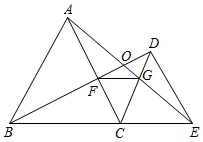A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. PM2.5是指大气中直径小于或等于0.0000025m的颗粒物，将0.0000025用科学记数法表示为.

查看试题解析
12. 如图，在 $△ A B C$ 和 $△ F E D$ 中， $B D = E C$ ， $A B = F E$ ，当添加条件时，就可得到 $△ A B C ≌ △ E D F$ ．（只需填写一个即可）

查看试题解析
13. 若 $a^{m} = 8, a^{n} = \frac{1}{2}$ ，则 $a^{2 m - 3 n}$ ＝．

查看试题解析
14. 已知：如图△ABC中，∠B＝50°，∠C＝90°，在射线BA上找一点D ，使△ACD为等腰三角形，则∠ACD的度数为．

查看试题解析
15. 如图，已知射线OC上的任意一点到∠AOB的两边的距离都相等，点D、E、F分别为边OC、OA、OB上，如果要想证得OE=OF，只需要添加以下四个条件中的某一个即可，请写出所有可能的条件的序号．

①∠ODE=∠ODF；②∠OED=∠OFD；③ED=FD；④EF⊥OC．

查看试题解析

三、解答题

16. 计算：

(1)、 ${(- 2)}^{2} - | \sqrt{3} - 2 | - \sqrt{9} + \sqrt[3]{- 8}$

(2)、 $(15 x^{2} y - 10 x y^{2}) \div (- 5 x y)$

(3)、 $(x - 3) (x + 2) - {(x - 1)}^{2}$

查看试题解析
17. 如图所示，在图①和图②的网格中，小正方形的边长均为1．

(1)、请在图①中画出端点在格点的线段 $M N$ 和 $E F$ ，使 $M N = \sqrt{2}$ ， $E F = \sqrt{5}$ ，并选择其中的一个说明理由

(2)、如图②， $△ A B C$ 是一个格点三角形，这个三角形是直角三角形吗？为什么？

查看试题解析
18. 分解因式：

(1)、 $5 x^{2} + 10 x + 5$

(2)、 $4 a^{2} (x - y) + 9 b^{2} (y - x)$

查看试题解析
19. 襄汾县教科局“有效学习儒家文化”课题于今年结题，在这次结题活动中，甲、乙两校师生共150人进行了汇报演出，小林将甲、乙两校参加各项演出的人数绘制成如下不完整的统计图表，根据提供的信息解答下列问题：
甲校参加汇报演出的师生人数统计表

百分比

人数

话剧

50%

m

演讲

12%

6

其他

n

19

甲、乙两校参加汇报演出的师生人数统计图

(1)、 $m =$ ， $n =$ ；

(2)、计算乙校的扇形统计图中“话剧”的 $∠ 1$ 度数；

(3)、哪个学校参加“话剧”的师生人数多？说明理由．

查看试题解析
20. 如图，在 $Δ A B C$ 中， $∠ A = 60^{\circ}$

⑴尺规作图：作 $∠ A B C$ 的平分线 $l_{1}$ ；

⑵尺规作图：作线段 $B C$ 的垂直平分线 $l_{2}$ ；（不写作法，保留作图痕迹）

⑶若 $l_{1}$ 与 $l_{2}$ 交于点 $P$ ，∠ACP=24°，求 $∠ A B P$ 的度数.

查看试题解析
21. 阅读下列材料，并回答问题，事实上，在任何一个直角三角形中，两条直角边的平方之和一定等于斜边的平方，这个结论就是著名的勾股定理．请利用这个结论，完成下面活动：

(1)、一个直角三角形的两条直角边分别为6、8，那么这个直角三角形斜边长为．

(2)、如图， $A D ⊥ B C$ 于 $D$ ， $A D = B D$ ， $A C = B E$ ， $A C = 3$ ， $D C = 1$ ，求 $B D$ 的长度．

(3)、如图，点 $A$ 在数轴上表示的数是多少？请用类似的方法在图数轴上画出表示数 $\sqrt{10}$ 的 $B$ 点（保留作图痕迹）

查看试题解析
22. 阅读：已知a、b、c为 $△ A B C$ 的三边长，且满足 $a^{2} c^{2} - b^{2} c^{2} = a^{4} - b^{4}$ ，试判断 $△ A B C$ 的形状．
（解析）解：因为 $a^{2} c^{2} - b^{2} c^{2} = a^{4} - b^{4}$ ，①

所以 $c^{2} (a^{2} - b^{2}) = (a^{2} - b^{2}) (a^{2} + b^{2})$ ②

所以 $c^{2} = a^{2} + b^{2}$ ③

所以 $△ A B C$ 是直角三角形④

请据上述解题回答下列问题：

(1)、上述解题过程，从第步（该步的序号）开始出现错误，错的原因为；

(2)、请你将正确的解答过程写下来．

查看试题解析
23. 知识背景
我们在第十一章《三角形》中学习了三角形的边与角的性质，在第十二章《全等三角形》中学习了全等三角形的性质和判定，在十三章《轴对称》中学习了等腰三角形的性质和判定．在一些探究题中经常用以上知识转化角和边，进而解决问题

(1)、问题初探
如图（1），△ABC中，∠BAC＝90°，AB＝AC ，点D是BC上一点，连接AD ，以AD为一边作△ADE ，使∠DAE＝90°，AD＝AE ，连接BE ，猜想BE和CD有怎样的数量关系，并说明理由．

(2)、类比再探
如图（2），△ABC中，∠BAC＝90°，AB＝AC ，点M是AB上一点，点D是BC上一点，连接MD ，以MD为一边作△MDE ，使∠DME＝90°，MD＝ME ，连接BE ，则∠EBD＝．（直接写出答案，不写过程，但要求作出辅助线）

(3)、方法迁移
如图（3），△ABC是等边三角形，点D是BC上一点，连接AD ，以AD为一边作等边三角形ADE ，连接BE ，则BD、BE、BC之间有怎样的数量关系？（直接写出答案，不写过程）．

(4)、拓展创新
如图（4），△ABC是等边三角形，点M是AB上一点，点D是BC上一点，连接MD ，以MD为一边作等边三角形MDE ，连接BE ．猜想∠EBD的度数，并说明理由．

查看试题解析

	百分比	人数
话剧	50%	m
演讲	12%	6
其他	n	19