山西省晋中市寿阳县2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-10-13 类型:期末考试
一、单选题
-
1. 的值是( )A、4 B、2 C、±4 D、±22. 下列各式计算正确的是( )A、 B、 C、 D、3. 两千多年前,古希腊数学家欧几里得首次运用某种数学思想整理了几何知识,完成 了数学著作《原本》,欧几里得首次运用的这种数学思想是( )A、公理化思想 B、数形结合思想 C、抽象思想 D、模型思想4. 已知 是方程 的解,则m的值( )A、2 B、 C、1 D、5. 某演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例计算选手的综合成绩.某选手的演讲内容、演讲能力、演讲效果成绩依次为85、90、95,则该选手的综合成绩为( )A、92 B、88 C、90 D、956. 用代入法解方程组 下面四个选项中正确的是( )A、由②得 ,再代入① B、由②得 ,再代入① C、由①得 ,再代入② D、由①得 ,再代入②7. 已知正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=-kx+k的图像大致是( )A、
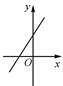 B、
B、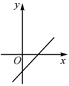 C、
C、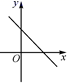 D、
D、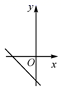 8. 满足下列条件的 中,不是直角三角形的是( )A、 B、 , , C、 , , D、 , ,9. 张翔从学校出发骑自行车去县城,中途因道路施工步行了一段路, 后到达县城.他骑车的平均速度是 ,步行的平均速度是 ,路程全长 .他骑车与步行各走了多少千米?设他骑自行车行了 ,步行走了 ,则可列方程组为( )A、 B、 C、 D、10. 如图,在 ABC中,∠B+∠C=α,按图进行翻折,使 ,则∠ FE的度数是( )
8. 满足下列条件的 中,不是直角三角形的是( )A、 B、 , , C、 , , D、 , ,9. 张翔从学校出发骑自行车去县城,中途因道路施工步行了一段路, 后到达县城.他骑车的平均速度是 ,步行的平均速度是 ,路程全长 .他骑车与步行各走了多少千米?设他骑自行车行了 ,步行走了 ,则可列方程组为( )A、 B、 C、 D、10. 如图,在 ABC中,∠B+∠C=α,按图进行翻折,使 ,则∠ FE的度数是( ) A、 B、90°﹣ C、α﹣90° D、2α﹣180°
A、 B、90°﹣ C、α﹣90° D、2α﹣180°二、填空题
-
11. 把 化成最简二次根式为.12. 请将命题“对顶角相等”改写为“如果……,那么……”的形式: .13. 如图,一次函数 和 的图象交于点 .则关于 , 的二元一次方程组 的解是 .
 14. 如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为 .
14. 如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为 . 15. 如图(1),在△ABC中,AB=AC . 动点P从△ABC的顶点A出发,以 的速度沿 匀速运动回到点A . 图(2)是点P运动过程中,线段AP的长度 随时间 变化的图象,其中点Q为曲线部分的最低点.当P点回到点A 时,全程所用的时间为 .
15. 如图(1),在△ABC中,AB=AC . 动点P从△ABC的顶点A出发,以 的速度沿 匀速运动回到点A . 图(2)是点P运动过程中,线段AP的长度 随时间 变化的图象,其中点Q为曲线部分的最低点.当P点回到点A 时,全程所用的时间为 .
三、解答题
-
16. 计算:(1)、(2)、17. 解方程组(1)、(2)、解方程组
Ⅰ、小组合作时,发现有同学这么做:①×2得4x-10y=-42③,②-③得3y-(-10y)=23-(-42) 解之得y=5,代入①得x= ▲ ,
∴这个方程组的解是 ▲ , 该同学解这个方程组的过程中使用了 ▲ 消元法,目的是把二元一次方程转化为 ▲ ;
Ⅱ、请你用另一种方法解这个方程组.
18. 如图,三角形ABC中,AC=BC , D是BC上的一点,连接AD , DF平分∠ADC交∠ACB的外角∠ACE的平分线于F . 求证:CF AB . 19. 8年级某老师对一、二班学生阅读水平进行测试,并将成绩进行了统计,绘制了如下图表(得分为整数,满分为10分,成绩大于或等于6分为合格,成绩大于或等于9分为优秀).
19. 8年级某老师对一、二班学生阅读水平进行测试,并将成绩进行了统计,绘制了如下图表(得分为整数,满分为10分,成绩大于或等于6分为合格,成绩大于或等于9分为优秀).
班级
平均分
方差
中位数
众数
合格率
优秀率
一班
a
2.11
7
c
92.5%
20%
二班
6.85
4.28
b
8
d
10%
根据图表信息,回答问题:
(1)、直接写出表中a,b,c,d的值;(2)、用方差推断,班的成绩波动较大;用优秀率和合格率推断,班的阅读水平更好些;(3)、甲同学用平均分推断,一班阅读水平更好些;乙同学用中位数或众数推断,二班阅读水平更好些。你认为谁的推断比较科学合理,更客观些,为什么?20. 我国传统数学名著《九章算术》记载:“今有牛五、羊二,直金十九两;牛二、羊五,直金十六两.问牛、羊各直金几何?”译文:“假设有5头牛、2只羊,值19两银子;2头牛、5只羊,值16两银子,问每头牛、每只羊分别值银子多少两?”根据以上译文,提出以下两个问题:
(1)、求每头牛、每只羊各值多少两银子?(2)、若某商人准备用19两银子买牛和羊(要求既有牛也有羊,且银两须全部用完),请问商人有几种购买方法?列出所有的可能.21. 甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)是一次函数关系,如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500 元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.
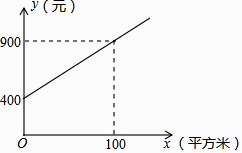 (1)、求如图所示的y与x的函数解析式:(不要求写出定义域);(2)、如果某学校目前的绿化面积是1200平方米,试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.22. 问题情境:在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含 角的直角三角尺 ”为主题开展数学活动.
(1)、求如图所示的y与x的函数解析式:(不要求写出定义域);(2)、如果某学校目前的绿化面积是1200平方米,试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.22. 问题情境:在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含 角的直角三角尺 ”为主题开展数学活动.操作发现:
 (1)、如图1,小明把三角尺的 角的顶点G放在CD上,若 ,求 的度数;(2)、如图2,小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明 与 之间的数量关系;
(1)、如图1,小明把三角尺的 角的顶点G放在CD上,若 ,求 的度数;(2)、如图2,小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明 与 之间的数量关系;四、结论应用: (3)如图3,小亮把三角尺的直角顶点F放在CD上, 角的顶点E落在AB上.若 ,求 的度数 用含 的式子表示 . 【答案】解:∵AB∥CD, ∴∠AEF+∠CFE=180°,即∠AEG+∠FEG+∠EFG+∠GFC=180°. 又∵∠GFE=90°,∠GEF=30°,∠AEG=α, ∴∠GFC=180°﹣90°﹣30°﹣α=60°﹣α. 【解析】【分析】 【题型】综合题 【分值】 【考查类型】常考题 【试题级别】八年级
-
23. 如图1,平面直角坐标系中,直线y=kx+b与x轴交于点A(6,0),与y轴交于点B , 与直线y=2x交于点C(a , 4).
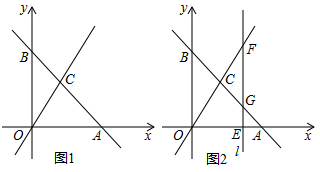 (1)、求点C的坐标及直线AB的表达式;(2)、如图2,在x轴上有一点E , 过点E作直线 ⊥x轴,交直线y=2x于点F , 交直线y=kx+b于点G , 若GF的长为3.求点E的坐标;(3)、在y轴上是否存在一点F , 使以O、C、F为顶点的三角形是等腰三角形,若存在,直接写出点F的坐标;若不存在,说明理由.
(1)、求点C的坐标及直线AB的表达式;(2)、如图2,在x轴上有一点E , 过点E作直线 ⊥x轴,交直线y=2x于点F , 交直线y=kx+b于点G , 若GF的长为3.求点E的坐标;(3)、在y轴上是否存在一点F , 使以O、C、F为顶点的三角形是等腰三角形,若存在,直接写出点F的坐标;若不存在,说明理由.