山西省晋中市祁县2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-10-13 类型：期末考试

进入出卷网下载

一、单选题

1. 16的平方根是（　　）

A、±8 B、±4 C、4 D、﹣4

查看试题解析
2. 下列计算结果正确的是（）

A、 $3 \sqrt{2} - \sqrt{2} = 3$ B、 $\sqrt{12} \div \sqrt{3} = 2$ C、 ${(2 \sqrt{3})}^{2} = 6$ D、 $\sqrt{{(- 3)}^{2}} = - 3$

查看试题解析
3. 如图，将一副三角尺按如图所示方式摆放，点A ， B ， D在同一条直线上， $E F / / A D$ ， $∠ C A B = ∠ E D F = 90 °$ ， $∠ C = 45 °$ ， $∠ E F D = 30 °$ ， $∠ B F D$ 的度数是（）

A、 $15 °$ B、 $20 °$ C、 $30 °$ D、 $45 °$

查看试题解析
4. 比赛中，评分时经常要“去掉一个最高分，去掉一个最低分”，所剩数据与原数据比较不受影响的是（）

A、众数 B、中位数 C、平均数 D、方差

查看试题解析
5. 下列命题中，假命题是（）

A、对顶角相等 B、全等三角形的面积相等 C、如果 $a^{2} = b^{2}$ 那么 $a = b$ D、直角三角形的两锐角互余

查看试题解析
6. 函数y= $\frac{1}{\sqrt{x - 1}}$ 的自变量x的取值范围在数轴上可表示为（　　）

A、 B、 C、 D、

查看试题解析
7. 要画出一次函数 $y = k x + b$ 的图象，列表如下，下列结论正确的是（）

x

…

$- 1$

0

1

2

…

y

…

5

2

$- 1$

$- 4$

…

A、y随x的增大而增大 B、方程 $k x + b = 2$ 的解是 $x = - 4$ C、一次函数 $y = k x + b$ 的图象经过二、三、四象限 D、一次函数 $y = k x + b$ 的图象与y轴的交点是 $(0 ， 2)$

查看试题解析
8. 《九章算术》中有这样一个问题：“今有甲乙二人持钱不知其数，甲得乙半而钱五十，乙得甲太半而钱亦五十.问甲、乙持钱各几何？”题意为：今有甲乙二人，不知其钱包里有多少钱，若乙把其一半的钱给甲，则甲的钱数为50；而甲把其 $\frac{2}{3}$ 的钱给乙，则乙的钱数也能为50，问甲、乙各有多少钱？设甲的钱数为x，乙的钱数为y，则列方程组为（）

A、 ${\begin{array}{l} x + \frac{1}{2} y = 50 \\ y + \frac{2}{3} x = 50 \end{array}$ B、 ${\begin{array}{l} y + \frac{1}{2} y = 50 \\ x + \frac{2}{3} x = 50 \end{array}$ C、 ${\begin{array}{l} x - \frac{1}{2} y = 50 \\ y - \frac{2}{3} x = 50 \end{array}$ D、 ${\begin{array}{l} y - \frac{1}{2} y = 50 \\ x - \frac{2}{3} x = 50 \end{array}$

查看试题解析
9. 如图，某电信公司提供了A ， B两种方案的移动通讯费用y（元）与通话时间x（元）之间的关系，则下列结论中正确的是（）
①若通话时间少于120分，则A方案便宜②若通话时间超过200分，则B方案便宜③若通讯费用为50元，则A方案的通话时间多④若超出免费时长，两种方案通讯每分钟加收费用相同

A、①② B、①②③ C、①②④ D、②③④

查看试题解析
10. 如图①，在边长为 $4cm$ 的正方形 $A B C D$ 中，点P以每秒 $2cm$ 的速度从点A出发，沿 $A B \to B C$ 的路径运动，到点C止，过点P作 $P Q / / B D$ ， $P O$ 与边 $A D$ （或边 $C D$ ）交于点Q ， $P Q$ 的长度 $y (cm)$ 与点P的运动时间x（秒）的函数图象如图②所示，当点P运动2.5秒时， $P Q$ 的长度是（） $cm$ ．

A、2 B、3 C、 $\sqrt{2}$ D、 $3 \sqrt{2}$

查看试题解析

二、填空题

11. 如果不等式 $(a - 2) x > a - 2$ 的解集是 $x < 1$ ，那么a必须满足．

查看试题解析
12. 若数据10，9，a，12，9的平均数是10，则这组数据的方差是

查看试题解析
13. 《勾股》中记载了这样一个问题：“今有开门去阃（kǔn）一尺不合2寸，问门广几何？”意思是：如图推开两扇门（ $A D$ 和 $B C$ ），门边沿D ， C两点到门槛 $A B$ 的距高是1尺（1尺=10寸），两扇门的间隙 $C D$ 为2寸，则门槛 $A B$ 为寸．

查看试题解析
14. 一次函数 $y = k x + b$ 与一次函数 $y = x + 3$ 的图象如图所示，那么方程组 ${\begin{array}{l} y = k x + b \\ y = x + 3 \end{array}$ 的解是．

查看试题解析
15. 如图，已知a，b，c分别是Rt△ABC的三条边长，∠C=90°，我们把关于x的形如y= $\frac{a}{c} x + \frac{b}{c}$ 的一次函数称为“勾股一次函数”，若点P（1， $\frac{3 \sqrt{5}}{5}$ ）在“勾股一次函数”的图象上，且Rt△ABC的面积是5，则c的值是．

查看试题解析

三、解答题

16. 化简与计算

(1)、 $\sqrt{27} \times \sqrt{3} - \frac{\sqrt{18} + \sqrt{8}}{\sqrt{2}}$

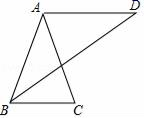
(2)、 $\frac{1}{\sqrt{2} - 1} - {(3 - \sqrt{2})}^{2}$

查看试题解析
17.

(1)、解不等式组 ${\begin{array}{l} 2 x - 1 < 5 \\ \frac{3 + x}{2} - 1 ⩽ \frac{4 x + 3}{6} \end{array}$

(2)、解方程组 ${\begin{array}{l} 3 x + 2 y = 17 \\ 2 (x + 1) - y = 11 \end{array}$

查看试题解析
18. 如图，在△ABC中，∠BAC=40°，∠C=70°，BD平分∠ABC，且∠ADB=35°，求证：AD∥BC．

查看试题解析
19. 某跳水队为了解运动员的年龄情况，作了一次年龄调查，根据跳水运动员的年龄（单位：岁），绘制出如下的统计图①和图②请根据相关信息，解答下列问题：

(1)、本次接受调查的跳水运动员人数为，图①中m的值为；

(2)、这组跳水运动员年龄众数为，中位数；

(3)、求这组数据的平均数．

查看试题解析
20. 某景点南北两个游客集散点之间有A、B两种摆渡车通行，某天，摆渡车A从北集散点出发，匀速行驶到南集散点，同时摆渡车B从南集散点出发，运送一批游客匀速行驶到北集散点，两摆渡车距南集散点的距离y（千米）与行驶时间x（分钟）之间的函数关系图象如图所示．
请根据图象解决下列问题：

(1)、南北两个集散点之间的距离是千米；

(2)、求出摆渡车B距南集散点的距离y（千米）与x（分钟）之间的函数关系式；

(3)、点M的坐标为，它表示的实际意义是．

查看试题解析
21. 在经济双循环的政策导引下，某汽车专卖店新推出A ， B两种型号的新能源汽车．上周售出1辆A型车和3辆B型车，销售额为54万元；本周已售出2辆型车和1辆B型车，销售额为48万元．

(1)、求每辆A型车和B型车的售价各为多少万元？

(2)、甲公司拟向该店购买A、B两种型号的新能源汽车共6辆，且A型号汽车不少于4辆，购车费不超过105万元，有哪几种购车方案？

查看试题解析
22. 问题1：现有一张△ABC纸片，点D、E分别是△ABC边上两点，若沿直线DE折叠．

(1)、探究1：如果折成图①的形状，使A点落在CE上，则∠1与∠A的数量关系是；

(2)、探究2：如果折成图②的形状，猜想∠1+∠2和∠A的数量关系是；

(3)、探究3：如果折成图③的形状，猜想∠1、∠2和∠A的数量关系，并说明理由．

(4)、问题2：将问题1推广，如图④，将四边形ABCD纸片沿EF折叠，使点A、B落在四边形EFCD的内部时，∠1+∠2与∠A、∠B之间的数量关系是.

查看试题解析
23. 综合与实践
如图①，已知直线 $y = 3 x + 3$ 与x轴，y轴分别交于B ， A两点以B为直角顶点在第二象限内部作等腰 $R t △ A B C$ ，完成下列任务：

(1)、点C的坐标为；

(2)、求直线 $A C$ 的关系式；

(3)、如图②，直线 $A C$ 交x轴于M ，点 $P (- 3 ， a)$ 是线段 $B C$ 上一点，在线段 $B M$ 上是否存在一点N ，使直线 $P N$ 平分 $△ B C M$ 的面积？若存在，请求出点N的坐标；若不存在，请说明理由．

查看试题解析

x	…	$- 1$	0	1	2	…
y	…	5	2	$- 1$	$- 4$	…