山西省晋城市阳城县2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-10-13 类型:期末考试
一、单选题
-
1. 下列运算中,结果正确的是( )A、 B、 C、 D、2. 下列说法错误的是( )A、 中的a可以是正数、负数、零 B、 中的a不可能是负数 C、数a的平方根一定有两个,它们互为相反数 D、数a的立方根只有一个3. 估算 在( )A、5与6之间 B、6与7之间 C、7与8之间 D、8与9之间4. 如图,点B、E、C、F在同一条直线上, , ,要用SAS证明 ≌ ,可以添加的条件是
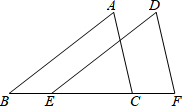 A、 B、 C、 D、5. 给出下面四个命题中,其中真命题的个数是( )
A、 B、 C、 D、5. 给出下面四个命题中,其中真命题的个数是( )⑴全等三角形的对应边相等
⑵所有的等边三角形都全等
⑶同旁内角互补
⑷所有定理的逆命题都是真命题
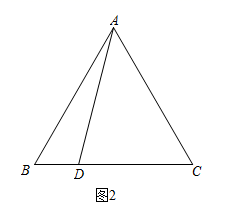
A、1个 B、2个 C、3个 D、4个6. 下列因式分解正确的是( )A、 B、 C、 D、7. 如图,在 中,AB、AC的垂直平分线分别交BC于点E、F,若 ,则 为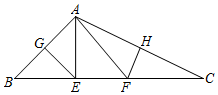 A、 B、 C、 D、8. 如图,在 中, ,对角线 与 相交于点O, 交 于E,若 的周长为 ,则 的周长是( )
A、 B、 C、 D、8. 如图,在 中, ,对角线 与 相交于点O, 交 于E,若 的周长为 ,则 的周长是( )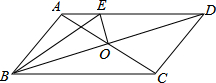 A、 B、 C、 D、无法确定9. 如图,2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的《勾股圆方图》(也称《赵爽弦图》),它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么 的值为( )
A、 B、 C、 D、无法确定9. 如图,2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的《勾股圆方图》(也称《赵爽弦图》),它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么 的值为( )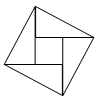 A、13 B、19 C、25 D、16910. 程老师制作了如图1所示的学具,用来探究“边边角条件是否可确定三角形的形状”问题,操作学具时,点Q在轨道槽AM上运动,点P既能在以A为圆心、以8为半径的半圆轨道槽上运动,也能在轨道槽QN上运动,图2是操作学具时,所对应某个位置的图形的示意图.
A、13 B、19 C、25 D、16910. 程老师制作了如图1所示的学具,用来探究“边边角条件是否可确定三角形的形状”问题,操作学具时,点Q在轨道槽AM上运动,点P既能在以A为圆心、以8为半径的半圆轨道槽上运动,也能在轨道槽QN上运动,图2是操作学具时,所对应某个位置的图形的示意图.
有以下结论:
①当∠PAQ=30°,PQ=6时,可得到形状唯一确定的△PAQ
②当∠PAQ=30°,PQ=9时,可得到形状唯一确定的△PAQ
③当∠PAQ=90°,PQ=10时,可得到形状唯一确定的△PAQ
④当∠PAQ=150°,PQ=12时,可得到形状唯一确定的△PAQ

其中所有正确结论的序号是( )
A、②③ B、③④ C、②③④ D、①②③④二、填空题
-
11. 4的平方根是12. 已知 , ,则 的值是 .13. 已知 ,则 .14. 在实数 , , , , , 中,无理数有个.15. 命题:“如果两直线平行,那么同旁内角互补”的逆命题为 .16. 若x2-y2=48,x+y=6,则3x-3y= .17. .18. 一只蚂蚁从长、宽都是3cm,高是8cm的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是cm.
 19. 现有A、B、C三种型号的地板砖,其规格如图所示,若用这三种地板砖铺设一个长为 ,宽为 的长方形地面,则需要B种地砖块.
19. 现有A、B、C三种型号的地板砖,其规格如图所示,若用这三种地板砖铺设一个长为 ,宽为 的长方形地面,则需要B种地砖块.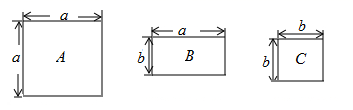 20. 如图,在 中, , 是 的角平分线,交 于点N, ,若 , ,则 .
20. 如图,在 中, , 是 的角平分线,交 于点N, ,若 , ,则 .
三、解答题
-
21. 计算:(1)、(2)、22. 先化简,再求值:
,(其中 )
23. 因式分解:(1)、(2)、24. 如图,已知平行四边形 . (1)、用直尺和圆规作出 的平分线 ,交 的延长线于点E,交 于点F(保留作图痕迹,不写作法);(2)、在第(1)题的条件下,求证: 是等腰三角形.25. 如图,点D、B分别在∠A的两边上,C是∠A内一点,且AB=AD,BC=DC,CE⊥AD,CF⊥AB,垂足分别为E、F.
(1)、用直尺和圆规作出 的平分线 ,交 的延长线于点E,交 于点F(保留作图痕迹,不写作法);(2)、在第(1)题的条件下,求证: 是等腰三角形.25. 如图,点D、B分别在∠A的两边上,C是∠A内一点,且AB=AD,BC=DC,CE⊥AD,CF⊥AB,垂足分别为E、F.求证:CE=CF.
 26. 当前新冠肺炎疫情形势依然复杂严峻,且病毒传播方式趋于多样化,为配合社区做好新冠疫情防控工作,提高防护意识,明明同学随机调查了她所在社区若干名居民的年龄,将调查数据绘制成如下扇形统计图和条形统计图.
26. 当前新冠肺炎疫情形势依然复杂严峻,且病毒传播方式趋于多样化,为配合社区做好新冠疫情防控工作,提高防护意识,明明同学随机调查了她所在社区若干名居民的年龄,将调查数据绘制成如下扇形统计图和条形统计图.请根据以下不完整的统计图提供的信息,解答下列问题:

社区人员出入情况统计表
出入人员年龄段
0~14
15~40
41~59
60岁及以上
出现次数
18
55
43
12
(1)、明明同学共调查了名居民的年龄,扇形统计图中 .(2)、补全条形统计图,并注明人数.(3)、若该社区年龄在0~14岁的居民约有350人,请估计该辖区居民总人数是人.(4)、为进一步掌握该社区中人员出入情况,明明又随机调查了128人.情况如下表,那么年龄是60岁及以上老人出入的频率是 . (精确到小数点后一位)