浙江省杭州市2021年九年级下学期数学中考一模试卷
试卷更新日期:2021-10-13 类型:中考模拟
一、单选题
-
1. 下列四个图形中,为中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 2021年春节,为了预防新冠肺炎疫情,各地纷纷响应“原地过年”的倡导,假期七天,全国铁路,公路,水路,民航共发送旅客大约98400000人次,比去年同期下降 .数据98400000用科学记数法表示为( )A、 B、 C、 D、3. 如图,直线 ,直线AC交 于点A,B,C,直线DF交 于点D,E,F.若 ,则 的值为( )
2. 2021年春节,为了预防新冠肺炎疫情,各地纷纷响应“原地过年”的倡导,假期七天,全国铁路,公路,水路,民航共发送旅客大约98400000人次,比去年同期下降 .数据98400000用科学记数法表示为( )A、 B、 C、 D、3. 如图,直线 ,直线AC交 于点A,B,C,直线DF交 于点D,E,F.若 ,则 的值为( )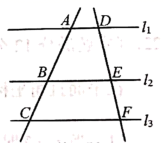 A、 B、 C、 D、4. 不等式 的解集在数轴上表示正确的是( )A、
A、 B、 C、 D、4. 不等式 的解集在数轴上表示正确的是( )A、 B、
B、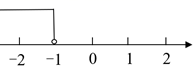 C、
C、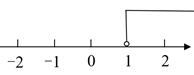 D、
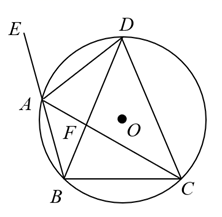
D、 5. 在 中, ,则 的正弦值为( )A、 B、 C、2 D、6. 如图, ,则 的度数为( )
5. 在 中, ,则 的正弦值为( )A、 B、 C、2 D、6. 如图, ,则 的度数为( )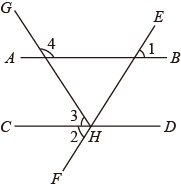 A、 B、 C、 D、7. 某校元旦文艺演出中,10位评委给某个节目的评分各不相同,去掉1个最高分和1个最低分,剩下的8个评分与原始的10个评分相比,( )A、平均数不发生变化 B、中位数不生变化 C、方差不发生变化 D、平均数和中位数都不发生变化8. 一次足球训练中,小明从球门正前方将球射向球门,球射向球门的路线呈抛物线,当球飞行的水平距离为 时,球达到最高点,此时球离地面 .已知球门高是 ,若足球能射入球门,则小明与球门的距离可能是( )A、 B、 C、 D、9. 如图,在 中, ,CD是 的角平分线,过点D作 交BC于点E. 和 的面积分别为 和 ,若 ,则 的值为( ).
A、 B、 C、 D、7. 某校元旦文艺演出中,10位评委给某个节目的评分各不相同,去掉1个最高分和1个最低分,剩下的8个评分与原始的10个评分相比,( )A、平均数不发生变化 B、中位数不生变化 C、方差不发生变化 D、平均数和中位数都不发生变化8. 一次足球训练中,小明从球门正前方将球射向球门,球射向球门的路线呈抛物线,当球飞行的水平距离为 时,球达到最高点,此时球离地面 .已知球门高是 ,若足球能射入球门,则小明与球门的距离可能是( )A、 B、 C、 D、9. 如图,在 中, ,CD是 的角平分线,过点D作 交BC于点E. 和 的面积分别为 和 ,若 ,则 的值为( ).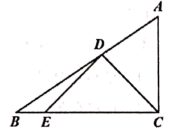 A、3 B、 C、 D、
A、3 B、 C、 D、二、填空题
-
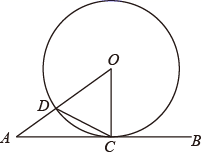
10. 若分式 有意义,则x的取值范围是.11. 已知-2是关于 的方程 的解,则 .12. 如图,直线AB与 相切于点C,AO交 于点D,连接CD,OC.若 ,则 .
 13. 西湖文化广场内有浙江省博物馆武林馆区,浙江省科技馆,浙江自然博物馆,小明和小皓要去展馆做志愿者,每人只选择去1个展馆,则他们在同一个展馆做志愿者的概率是 , 至少有一人在浙江自然博物馆的概率是.14. 如图,小明想要测量学校旗杆AB的高度,他发现系在旗杆顶端的绳子垂到了地面,从而测得绳子比旗杆长a米,小明将这根绳子拉直,绳子的末端落在地面的点C处,点C距离旗杆底部b米( ),则旗杆AB的高度为米(用含a,b的代数式表示).
13. 西湖文化广场内有浙江省博物馆武林馆区,浙江省科技馆,浙江自然博物馆,小明和小皓要去展馆做志愿者,每人只选择去1个展馆,则他们在同一个展馆做志愿者的概率是 , 至少有一人在浙江自然博物馆的概率是.14. 如图,小明想要测量学校旗杆AB的高度,他发现系在旗杆顶端的绳子垂到了地面,从而测得绳子比旗杆长a米,小明将这根绳子拉直,绳子的末端落在地面的点C处,点C距离旗杆底部b米( ),则旗杆AB的高度为米(用含a,b的代数式表示).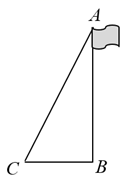 15. 在 中, ,点D是边AC上的动点(不与点A,C重合),将线段BD绕点B逆时针方向旋转到BE,使 ,连接AE.若点E在直线AC上,则 ;在点D移动的过程中,线段AE的最小值为.
15. 在 中, ,点D是边AC上的动点(不与点A,C重合),将线段BD绕点B逆时针方向旋转到BE,使 ,连接AE.若点E在直线AC上,则 ;在点D移动的过程中,线段AE的最小值为.三、解答题
-
16.(1)、计算: .(2)、解方程: .17. 在日历牌上,我们可以发现一些日期数满足一定的规律.如图是今年4月的日历牌,若任意选择图中上下相邻的四个日期(阴影部分),将其中四个位置上的数交叉相乘,再相减,例如: ,不难发现,结果都是7
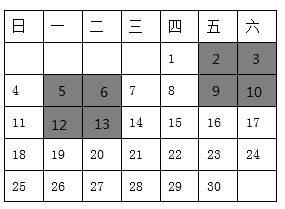 (1)、请再选择两个类似的部分试一试,看看是否符合这个规律(2)、设符合条件的四个日期左上角位置上的数为a,请利用整式的运算对以上的规律加以证明.18. 春季是传染病的高发期,某校为调查学生对传染病预防知识的了解情况,从全校学生中随机抽取了部分学生进行相关知识的测试,并将测试成绩(x)分为五个等级: ,整理后分别绘制成如图所示的频数直方图和扇形统计图(部分信息不完整).
(1)、请再选择两个类似的部分试一试,看看是否符合这个规律(2)、设符合条件的四个日期左上角位置上的数为a,请利用整式的运算对以上的规律加以证明.18. 春季是传染病的高发期,某校为调查学生对传染病预防知识的了解情况,从全校学生中随机抽取了部分学生进行相关知识的测试,并将测试成绩(x)分为五个等级: ,整理后分别绘制成如图所示的频数直方图和扇形统计图(部分信息不完整).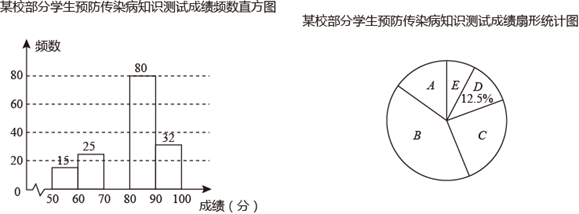 (1)、求测试等级为C的学生人数,并补全频数直方图.(2)、求扇形统计图中等级为B所对应的扇形圆心角的度数(3)、若全校1200名学生都参加测试,请根据抽样测试的结果,估计该校测试等级为A的学生有多少人?19. 如图,小明想要用撬棍撬动一块大石头,已知阻力为 ,阻力臂长为 .设动力为y(N),动力臂长为x(m).(杠杆平衡时,动力×动力臂=阻力×阻力臂,图中撬棍本身所受的重力略去不计.)
(1)、求测试等级为C的学生人数,并补全频数直方图.(2)、求扇形统计图中等级为B所对应的扇形圆心角的度数(3)、若全校1200名学生都参加测试,请根据抽样测试的结果,估计该校测试等级为A的学生有多少人?19. 如图,小明想要用撬棍撬动一块大石头,已知阻力为 ,阻力臂长为 .设动力为y(N),动力臂长为x(m).(杠杆平衡时,动力×动力臂=阻力×阻力臂,图中撬棍本身所受的重力略去不计.)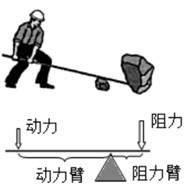 (1)、求y关于x的函数表达式.(2)、当动力臂长为 时,撬动石头至少需要多大的力?(3)、小明若想使动力不超过 ,在动力臂最大为 的条件下,他能否撬动这块石头?请说明理由.20. 如图,矩形ABCD的对角线AC,BD相交于点O,作 ,DE,CE相交于点E.
(1)、求y关于x的函数表达式.(2)、当动力臂长为 时,撬动石头至少需要多大的力?(3)、小明若想使动力不超过 ,在动力臂最大为 的条件下,他能否撬动这块石头?请说明理由.20. 如图,矩形ABCD的对角线AC,BD相交于点O,作 ,DE,CE相交于点E.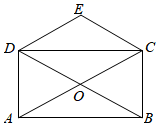 (1)、求证:四边形OCED是菱形.(2)、若矩形ABCD的面积为 , ,求点E到直线AB的距离.
(1)、求证:四边形OCED是菱形.(2)、若矩形ABCD的面积为 , ,求点E到直线AB的距离.