江苏省扬州市仪征市2021年数学中考二模试卷

试卷更新日期：2021-10-13 类型：中考模拟

进入出卷网下载

一、单选题

1. 实数2021的相反数是（）

A、2021 B、-2021 C、 $\frac{1}{2021}$ D、 $- \frac{1}{2021}$

查看试题解析
2. 下列计算结果为a⁶的是（）

A、a⁸﹣a² B、a³•a² C、a⁴+a² D、a⁸÷a²

查看试题解析
3. 二十四节气是历法中表示自然节律变化以及确立“十二月建”的特定节令，下面四幅设计作品分别代表“立春”、“芒种”、“白露”、“大雪”，其中轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如图是由几个小立方块所搭成的几何体的俯视图，小正方形中的数字表示该位置小立方块的个数，则该几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
5. 中国古代的《孙子兵法》中记载了一道广为人知的数学问题：现有一百匹马，一百片瓦，大马一匹可以驮三片瓦，小马三匹可以驮一片瓦，问有多少匹大马和多少匹小马？设有大马x匹，小马y匹，则下列方程正确的是（）

A、 ${\begin{array}{l} x + y = 100 \\ \frac{x}{3} + \frac{y}{3} = 100 \end{array}$ B、 ${\begin{array}{l} x + y = 100 \\ \frac{x}{3} + 3 y = 100 \end{array}$ C、 ${\begin{array}{l} x + y = 100 \\ 3 x + \frac{y}{3} = 100 \end{array}$ D、 ${\begin{array}{l} x + y = 100 \\ 3 x + 3 y = 100 \end{array}$

查看试题解析
6. 将一个边长为4cn的正方形与一个长，宽分别为8cm，2cm的矩形重叠放在一起，在下列四个图形中，重叠部分的面积最大的是（）

A、 B、 C、 D、

查看试题解析
7. 设a，b是正整数，满足a+b＞ab，给出以下四个结论：甲：a≠1且b≠1；乙：a＞1且b＞1；丙：a≠2且b≠2；丁：（a﹣1）（b﹣1）＝0.其中正确的结论是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
8. 已知点P（m，n）在直线y＝﹣x+2上，双曲线y＝ $\frac{k^{2} + 1}{x}$ （k为常数）图象经过点P，则2021m²﹣2020n²+2019k²的值是（）

A、4040 B、2020 C、﹣1 D、1

查看试题解析

二、填空题

9. 据统计，2021年五一黄金周里来自全国各地的游客超170000人涌入世园会.将170000用科学记数法表示应为.

查看试题解析
10. 分解因式： ${2a}^{2} - 4a + 2 =$ ．

查看试题解析
11. 若代数式 $\frac{1}{x - 1}$ 有意义，则实数x的取值范围是.

查看试题解析
12. 如果一个n边形的外角和是内角和的一半，那么 $n =$ .

查看试题解析
13. 已知圆锥的侧面积为10 $π$ cm² ．底面半径为2 cm，则圆锥的母线长为

查看试题解析
14. 如图所示的网格是正方形网格，图形的各个顶点均为格点，则∠1+∠2＝.

查看试题解析
15. 如图，点E是▱ABCD边AD的中点，连接AC、BE交于点P，过点P作PQ $//$ AD交CD于点Q，若AB＝3，则DQ＝.

查看试题解析
16. 如图，矩形ABCD，AB＝2，AD＝4，E是AD中点，连接BE、CE，分别以B、C为圆心，BE、CE为半径画弧交BC于点G、F，则图中阴影部分面积为.

查看试题解析
17. 如图，⊙O的圆心为原点，半径为2，反比例函数 $y = \frac{k}{x}$ （k≠0）图象与⊙O有两个交点，则k的取值是.

查看试题解析
18. 如图，Rt△ABC≌Rt△FDE，∠ABC＝∠FDE＝90°，∠BAC＝30°，AC＝4，将Rt△FDE沿直线l向右平移，连接BD、BE，则BD+BE的最小值为.

查看试题解析

三、解答题

19.

(1)、计算： $\sqrt{8}$ +（﹣1）⁰﹣4cos45°；

(2)、化简： $\frac{1}{1 - b} + \frac{b^{2}}{b - 1}$ .

查看试题解析
20. 解不等式组： ${\begin{matrix} 3 x < x + 4 \\ \frac{x - 2}{3} - 2 x < 1 \end{matrix}$ ，并写出它的非负整数解.

查看试题解析
21. 为了提高学生学习数学的兴趣，某校开展了一次数学趣味知识竞赛（竞赛成绩为百分制），并随机抽取了50名学生的竞赛成绩（本次竞赛没有满分），经过整理数据得到以下信息：
信息一：50名学生竞赛成绩频数分布直方图如图所示，从左到右依次为第一组到第五组（每组数据含前端点值，不含后端点值）.

信息二：第三组的成绩（单位：分）为74 71 73 74 79 76 77 76 76 73 72 75

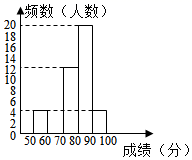
根据信息解答下列问题：

(1)、补全第二组频数分布直方图（直接在图中补全）；

(2)、第三组竞赛成绩的众数是分，抽取的50名学生竞赛成绩的中位数是分；

(3)、若该校共有1000名学生参赛，请估计该校参赛学生成绩不低于80分的约为人.

查看试题解析
22. 校本周日的上午和下午各开展一场“学党史、担使命”的知识演讲活动.小明、小红和小刚打算各自随机选择时间去观摩演讲.

(1)、小明在本周日上午去观摩演讲的概率为；

(2)、求小明、小红和小刚三人在同一个半天去观摩演讲的概率.

查看试题解析
23. 某物流仓储公司用A、B两种型号的机器人搬运物品，已知A型机器人比B型机器人每小时多搬25%，现A型机器人要搬运1000kg物品，B型机器人要搬运700kg物品.结果B型机器人提前1小时完成任务，求A、B型机器人每小时搬运多少千克的物品.

查看试题解析
24. 如图，△ABC中，AB＝CB.

(1)、作点B关于AC的对称点D；（要求：尺规作图，不写作法，保留作图痕迹）

(2)、在（1）所作的图中，连接AD，CD，连接BD，交AC于点O.
①猜想四边形ABCD的形状，并说明理由；

②取BC的中点E，连接OE、AE，若OE＝5，BO＝8，求线段AE的长.

查看试题解析
25. 如图，BD是四边形ABCD的对角线，BD⊥AD，⊙O是△ABD的外接圆，∠BDC＝∠BAD.

(1)、求证：CD是⊙O的切线；

(2)、连接OC交⊙O于点E，若AD＝2，CD＝6，cos∠BDC＝ $\frac{1}{3}$ ，求CE的长.

查看试题解析
26. 如图，在△ABC中，∠ABC＝90°，点P从点B向点A运动，点Q从点A向点C运动，两点同时出发，当点P到达点A时停止（同时点Q也停止），连接PQ，以PQ为边顺时针方向作正方形PQEF.已知AB＝10，tanA＝ $\frac{4}{3}$ ，BP＝AQ.

(1)、若点P运动到AB中点处，求正方形PQEF的边长；

(2)、若点E落在△ABC的一边上，求BP长；

(3)、在点P、Q的运动过程中，△APQ的面积是否存在最大值，若存在，请求出最大值，若不存在，请说明理由.

查看试题解析
27. 小明在学习函数的过程中遇到这样一个函数：y＝[x]，若x≥0时，[x]＝x²﹣1；若x＜0时，[x]＝﹣x+1.小明根据学习函数的经验，对该函数进行了探究.

(1)、下列关于该函数图象的性质正确的是；（填序号）
①y随x的增大而增大；

②该函数图象关于y轴对称；

③当x＝0时，函数有最小值为﹣1；

④该函数图象不经过第三象限.

(2)、①在平面直角坐标系xOy中画出该函数图象；
②若关于x的方程2x+c＝[x]有两个互不相等的实数根，请结合函数图象，直接写出c的取值范围是 ▲ ；

(3)、若点（a，b）在函数y＝x﹣3图象上，且﹣ $\frac{1}{2}$ ＜[a]≤2，则b的取值范围是.

查看试题解析
28. 苏科版教材中的折纸活动，引起了许多同学的兴趣.在折纸的过程中，同学们不仅发展了空间观念，还积累了数学活动经验.
[操作]：矩形ABCD，AB＝6，AD＝8，点M是边BC上一个动点，将△ABM沿AM折叠，折叠后点B的对应点为点B'.

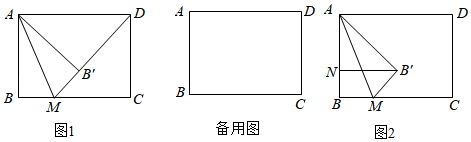
[发现]：（1）如图1，若点M、B'、D在同一条直线上，求证：△ADM为等腰三角形；

查看试题解析