江苏省盐城市建湖县2021年数学中考二模试卷

试卷更新日期：2021-10-13 类型：中考模拟

进入出卷网下载

一、单选题

1. 实数a与b在数轴上对应点的位置如图所示，则正确的结论是（）

A、a＜0 B、a＜b C、|a|＞|b| D、b＋3＞0

查看试题解析
2. 下列计算正确的是（）

A、a⁵•a²＝a⁷ B、2a＋a＝3a² C、（3a³）²＝6a⁶ D、（a²）³＝a⁵

查看试题解析
3. 某校九年级学生的平均年龄为16岁，年龄的方差为3，若学生人数没有变动，则两年前的同一批学生，对其年龄的说法正确的是（）

A、平均年龄为16岁，方差改变 B、平均年龄为14岁，方差不变 C、平均年龄为14岁，方差改变 D、平均年龄为16岁，方差不变

查看试题解析
4. 某冠状病毒直径为132nm（1nm＝10^－9m），则这种冠状病毒的直径（单位：m）用科学记数法表示为（）

A、132×10^－9 B、1.32×10^－6 C、1.32×10^－7 D、1.32×10^－8

查看试题解析
5. 将一副直角三角板（∠ACB＝∠EDF＝90°，∠A＝30°，∠F＝45°）按如图所示的位置放置，使得AB∥EF，则∠DOB的度数是（）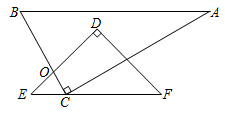

A、75° B、105° C、80° D、110°

查看试题解析
6. 如图，AB是⊙O的直径，点C、D都在⊙O上，若∠ABD＝63°、∠DCO＝24°，则∠BDC的度数是（）

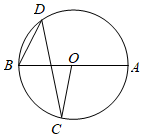A、15° B、24° C、39° D、63°

查看试题解析
7. 如图，在4×4的正方形网格中，记∠ABF＝ $α$ ，∠FCH＝ $β$ ，∠DGE＝ $γ$ ，则（）

A、 $β$ ＜ $α$ ＜ $γ$ B、 $β$ ≤ $γ$ ＜ $α$ C、 $α$ ＜ $γ$ ＜ $β$ D、 $α$ ＜ $β$ ＜ $γ$

查看试题解析
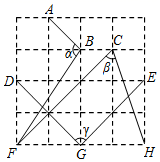8. 如图为某二次函数的部分图象，有如下四个结论：①此二次函数表达式为y＝ $\frac{1}{4}$ x²﹣x＋9：②若点B（﹣1，n）在这个二次函数图象上，则n＞m；③该二次函数图象与x轴的另一个交点为（﹣4，0）；④当0＜x＜5.5时，m＜y＜8.所有正确结论的序号是（）

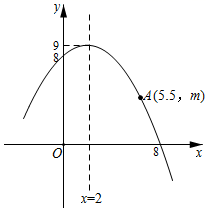A、①③ B、①④ C、②③ D、②④

查看试题解析

二、填空题

9. 二次根式 $\sqrt{4 - 2 x}$ 有意义，则x的取值范围是.

查看试题解析
10. 已知x＝﹣1是关于x的一元一次方程5x﹣3＝2m﹣8x的解，则m＝.

查看试题解析
11. 某单位招聘工作人员，考试分笔试和面试两部分，笔试成绩与面试成绩按6∶4记入总成绩，若小李笔试成绩为90分，面试成绩为80分，则他的总成绩是.

查看试题解析
12. 若一条长为32cm的细线能围成一边长等于8cm的等腰三角形，则该等腰三角形的腰长为cm.

查看试题解析
13. 设方程x²﹣2021x﹣1＝0的两个根分别为x₁、x₂ ，则x₁＋x₂﹣x₁x₂的值是.

查看试题解析
14. 如图是一长为12cm，宽为5cm的长方形木板，在桌面上作无滑动的翻滚（顺时针方向），木板上的点A位置变化为A→A₁→A₂ ，其中第二次翻滚时被桌面上另一小木块挡住，且使木板与桌面成30°角，则A翻滚到A₂时，共经过的路径长为cm.

查看试题解析
15. 如图，在平面直角坐标系中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为1∶3，点A、B、E在x轴上，若正方形BEFG的边长为6，则C点坐标为.

查看试题解析
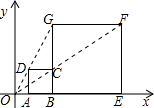16. 如图，⊙O的半径为10，A、D是圆上任意两点，且AD＝8，以AD为边作正方形ABCD（点C、O在直线AD两侧）若AD边绕点O旋转一周，则BC边扫过的面积为.

查看试题解析

三、解答题

17. 计算： $\sqrt{12} + {(\frac{1}{3})}^{- 1} - | - \sqrt{3} - 2 | - 4 \cos 30^{°}$ .

查看试题解析
18. 解不等式组5＋3x＜13； $\frac{x + 2}{3} - \frac{x - 1}{2} \leq 2$ ，并写出它的非负整数解.

查看试题解析
19. 已知关于x的一元二次方程x²﹣（m﹣2）x＋2m﹣8＝0.

(1)、求证：方程总有两个实数根.

(2)、若方程有一个根是负数，求m的取值范围.

查看试题解析
20. 某校在以“学党史、颂党恩、跟党走”为主题的校园文化艺术节期间，举办了A合唱，B舞蹈，C书法，D演讲共四个项目的比赛，要求每位学生必须参加且仅参加一项，数学兴趣小组的同学随机调查了部分学生的报名情况，并绘制了下列两幅不完整的统计图，请根据统计图中信息解答下列问题：

(1)、本次调查的学生总人数是人；扇形统计图中“D”部分的圆心角是.

(2)、请将条形统计图补充完整.

(3)、若全校共有1540名学生，请估计该校报名参加书法和演讲比赛的学生共有多少人？

查看试题解析
21. 五一期间，甲、乙两人计划在建湖附近的景点游玩，甲从A、B两个景点中任意选择一处游玩，乙从A、B、C三个景点中任意选择一处游玩.

(1)、乙恰好游玩A景点的概率为.

(2)、求甲、乙恰好游玩同一景点的概率.

查看试题解析
22. 如图1，点D在线段AB上，在△ABC和△ADE中，AB＝AC，DE＝DA，DE∥AC.

(1)、求证：BC∥AE；

(2)、若D为AB中点，请用无刻度的直尺在图2中作∠BAC的平分线AF.（保留画图痕迹，不写画法）

查看试题解析
23. 某中学为了创设“书香校园”，准备购买A、B两种书架，用于放置图书.在购买时发现，A种书架的单价比B种书架的单价多20元，用720元购买A种书架的个数与用600元购买B种书架的个数相同.

(1)、求A、B两种书架的单价各是多少元？

(2)、学校准备购买A、B两种书架共15个，且购买的总费用不超过1600元，求最多可以购买多少个A种书架？

查看试题解析
24. 如图，正比例函数y＝kx的图象与反比例函数y＝ $\frac{8}{x}$ （x＞0）的图象交于点A（a，4）.点B为x轴正半轴上一点，过B作x轴的垂线交反比例函数的图象于点C，交正比例函数的图象于点D.

(1)、求a的值及正比例函数y＝kx的表达式.

(2)、若CD＝6，求△ACD的面积.

查看试题解析
25. 如图，AB是⊙O的直径，AC是⊙O的一条弦，点P是⊙O上一点，且PA＝PC，PD∥AC，与BA的延长线交于点D.

(1)、求证：PD是⊙O的切线.

(2)、若tan∠PBA＝ $\frac{1}{3}$ ，AC＝12，求直径AB的长.

查看试题解析
26. 如图，在矩形ABCD中，AB＝6，BC＝8，点E是AD边上的动点，将矩形ABCD沿BE折叠，点A落在点A′处，连接A′C、A′D.

(1)、如图1，当AE＝时，A′D∥BE；

(2)、如图2，若AE＝3，求S_△A′CB.

(3)、点E在AD边上运动的过程中，∠A′CB的度数是否存在最大值，若存在，求出此时线段AE的长；若不存在，请说明理由.

查看试题解析
27. 如图，在平面直角坐标系xOy中，抛物线y＝x²＋bx＋c与x轴交于A、B两点，与y轴交于点C，对称轴为直线x＝2，点A的坐标为（1，0）.

(1)、求该抛物线的表达式及顶点坐标；

(2)、点P为抛物线上一点（不与点A重合），连接PC.当∠PCB＝∠ACB时，求点P的坐标；

(3)、在（2）的条件下，在对称轴上是否存在一点Q，连接PQ，将线段PQ绕点Q顺时针旋转90°，使点P恰好落在抛物线上？若存在，请求出点Q的坐标；若不存在，请说明理由.

查看试题解析