湖南省湘潭市2021年数学中考质检试卷(4月)
试卷更新日期:2021-10-13 类型:中考模拟
一、单选题
-
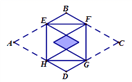
1. 如图,矩形EFGH的四个顶点分别在菱形ABCD的四条边上,BE=BF,将△AEH, △CFG分别沿EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的 时,则 为( )
 A、 B、2 C、 D、42. 我国探月工程嫦娥四号任务“鹊桥”中继星是世界首颗运行在地月 点 轨道的卫星,它的运行轨道距月球约65000公里,将65000用科学记数法表示应为( )A、 B、 C、 D、3. 下列运算,正确的是( )A、 B、 C、 D、4. 在同一平面直角坐标系中,函数 与 的图象可能是( ).A、
A、 B、2 C、 D、42. 我国探月工程嫦娥四号任务“鹊桥”中继星是世界首颗运行在地月 点 轨道的卫星,它的运行轨道距月球约65000公里,将65000用科学记数法表示应为( )A、 B、 C、 D、3. 下列运算,正确的是( )A、 B、 C、 D、4. 在同一平面直角坐标系中,函数 与 的图象可能是( ).A、 B、
B、 C、
C、 D、
D、 5. 如图, 是 的直径,且 , 是 上一点,将 沿直线 翻折,若翻折后的圆弧恰好经过点 ,则图中阴影部分的面积为( ).
5. 如图, 是 的直径,且 , 是 上一点,将 沿直线 翻折,若翻折后的圆弧恰好经过点 ,则图中阴影部分的面积为( ). A、 B、 C、 D、6. 如图,已知菱形OABC,OC在x轴上,AB交y轴于点D,点A在反比例函数 上,点B在反比例函数 上,且OD=2 ,则k的值为( )
A、 B、 C、 D、6. 如图,已知菱形OABC,OC在x轴上,AB交y轴于点D,点A在反比例函数 上,点B在反比例函数 上,且OD=2 ,则k的值为( ) A、3 B、 C、 D、7. 在棱长为2的正方体毛坯的一角处挖去一个棱长为1的小正方体,得到如图所示的几何体,这个几何体的俯视图是( )
A、3 B、 C、 D、7. 在棱长为2的正方体毛坯的一角处挖去一个棱长为1的小正方体,得到如图所示的几何体,这个几何体的俯视图是( ) A、
A、 B、
B、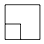 C、
C、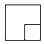 D、
D、 8. 如图,在⊙O中,点A、B、C在⊙O上,且∠ACB=110°,则∠α=( )
8. 如图,在⊙O中,点A、B、C在⊙O上,且∠ACB=110°,则∠α=( )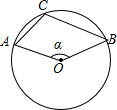 A、70° B、110° C、120° D、140°
A、70° B、110° C、120° D、140°二、填空题
-
9. 开学前,根据学校防疫要求,小明同学连续14天进行了体温测量,结果统计如下表:
体温(℃)
36.3
36.4
36.5
36.6
36.7
36.8
天数(天)
2
3
3
4
1
1

这组体温数据的中位数是℃.
10. 如图,在平行四边形 中, , , , 平分 交 于点 , 平分 交 于点 ,交 于点 ,连接 ,则 的长为. 11. 已知实数a,b,c满足a+b=ab=c,有下列结论:
11. 已知实数a,b,c满足a+b=ab=c,有下列结论:①若c≠0,则 =1;
②若a=3,则b+c=9;
③若a=b=c,则abc=0;
④若a,b,c中只有两个数相等,则a+b+c=8.
其中正确的是.(把所有正确结论的序号都选上)
12. 若代数式 有意义,则x的取值范围是 .13. 如图, 中, , , ,以点B为圆心,以BC长度为半径作弧,交BA于点D,以点C为圆心,以大于 为半径作弧,接着再以点D为圆心,以相同长度为半径作弧,两弧交于点E,作射线BE交CA于点F,以点B为圆心,以BF为长度作弧,交BA于点G,则阴影部分的面积为. 14. 在一个不透明的布袋中,装有红、黑、白三种只有颜色不同的小球,其中红色小球4个,黑、白色小球的数目相同.小明从布袋中随机摸出一球,记下颜色后放回布袋中,摇匀后随机摸出一球,记下颜色;…如此大量摸球实验后,小明发现其中摸出的红球的频率稳定于20%,由此可以估计布袋中的黑色小球有 个.15. 分解因式: = .16. 如图,已知在 中, ,点 , 在 上,且 ,请你在图中找出一组全等三角形.(不添加任何字母和辅助线)
14. 在一个不透明的布袋中,装有红、黑、白三种只有颜色不同的小球,其中红色小球4个,黑、白色小球的数目相同.小明从布袋中随机摸出一球,记下颜色后放回布袋中,摇匀后随机摸出一球,记下颜色;…如此大量摸球实验后,小明发现其中摸出的红球的频率稳定于20%,由此可以估计布袋中的黑色小球有 个.15. 分解因式: = .16. 如图,已知在 中, ,点 , 在 上,且 ,请你在图中找出一组全等三角形.(不添加任何字母和辅助线)
三、解答题
-
17. 计算: .18. 先化简,再求值: ÷(1+ ),其中x= +1.19. “校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
 (1)、接受问卷调查的学生共有人,扇形统计图中“了解”部分所对应的扇形的圆心角的度数为 ;(2)、若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为多少人?20. 如图, 是 的直径, 与 相交于点 , .
(1)、接受问卷调查的学生共有人,扇形统计图中“了解”部分所对应的扇形的圆心角的度数为 ;(2)、若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为多少人?20. 如图, 是 的直径, 与 相交于点 , . (1)、求证: 是 的切线.(2)、若 , ,求直径 的长度.21. 如图,某中学有一块三角形状的花圃ABC,现可直接测量到∠B=45°,∠C=30°,AC=8米.请你求出BC的长.(结果可保留根号)
(1)、求证: 是 的切线.(2)、若 , ,求直径 的长度.21. 如图,某中学有一块三角形状的花圃ABC,现可直接测量到∠B=45°,∠C=30°,AC=8米.请你求出BC的长.(结果可保留根号) 22.
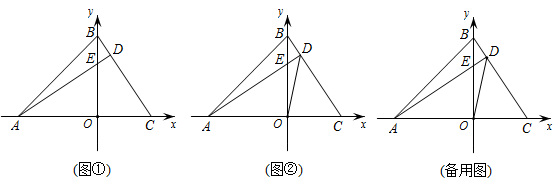
22.如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( , )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
 (1)、求抛物线的解析式;
(1)、求抛物线的解析式;
(2)、是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)、求△PAC为直角三角形时点P的坐标.