湖南省邵阳市邵阳县2021年初中毕业学业模拟考试数学试卷
试卷更新日期:2021-10-13 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、-2021 B、 C、 D、20212. 下列说法中不正确的是( )A、函数 的图象经过原点 B、函数 的图象位于第一、三象限 C、函数 的图象不经过第二象限 D、函数 的值随 的值的增大而减少3. 我市去年一季度国内生产总数值为468.15亿,这个数用科学记数法表示为( )A、 B、 C、 D、4. 如图,直线 ,直线 与 、 分别相交于点 , , 交 于点 ,若 ,则 的度数为( )
 A、30° B、40° C、50° D、60°5. 在△ 中,若 ,则 的度数是( )A、30° B、45° C、60° D、90°6. 如果 与 是同类项,那么 的值是( )A、 B、 C、1 D、37. 如图所示,正六棱柱的左视图是( )
A、30° B、40° C、50° D、60°5. 在△ 中,若 ,则 的度数是( )A、30° B、45° C、60° D、90°6. 如果 与 是同类项,那么 的值是( )A、 B、 C、1 D、37. 如图所示,正六棱柱的左视图是( )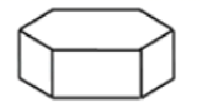 A、
A、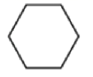 B、
B、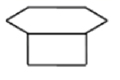 C、
C、 D、
D、 8. 学校决定从甲、乙两人中选一人去参加全县的射击比赛,在最后5次射击训练中,甲、乙两人的射击成绩分别为(单位:环)
8. 学校决定从甲、乙两人中选一人去参加全县的射击比赛,在最后5次射击训练中,甲、乙两人的射击成绩分别为(单位:环)甲:10 9 10 8 8
乙:7 9 10 10 9
则选谁去参加比赛更合适( )
A、甲、乙选谁都一样 B、选甲 C、选乙 D、无法确定9. 若正多边形的一个外角是36°,则该正多边形的内角和为( )A、360° B、720° C、1440° D、1800°10. 在同一平面直角坐标系中,函数 与 的大致图象可能为( )A、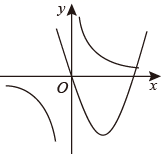 B、
B、 C、
C、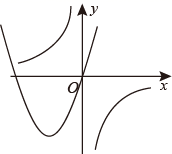 D、
D、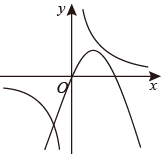
二、填空题
-
11. 化简 的结果是.12. 把 因式分解的结果是.13. 如图,△ABC经过位似变换得到△DEF,点O是位似中心且OA=AD,则△ABC与△DEF的面积比是.
 14. 若代数式 在实数范围内有意义,则x的取值范围是.15. 已知 , 满足方程组, ,则 的值为.16. 从3,-2,5这三个数中任取两个不同的数,作为点的坐标,则该点在第一象限的概率为.17. 如图,已知在 中, ,点 , 在 上,且 ,请你在图中找出一组全等三角形.(不添加任何字母和辅助线)
14. 若代数式 在实数范围内有意义,则x的取值范围是.15. 已知 , 满足方程组, ,则 的值为.16. 从3,-2,5这三个数中任取两个不同的数,作为点的坐标,则该点在第一象限的概率为.17. 如图,已知在 中, ,点 , 在 上,且 ,请你在图中找出一组全等三角形.(不添加任何字母和辅助线) 18. 如图所示,我国汉代数学家赵爽,为了证明勾股定理创制了一幅“弦图”,后人称其为“赵爽弦图”(如图),图由弦图变化得到,它是由八个全等的直角三角形拼接而成,记图中正方形 、正方形 、正方形 的面积分别为 、 、 .若正方形 的边长为5,则 .
18. 如图所示,我国汉代数学家赵爽,为了证明勾股定理创制了一幅“弦图”,后人称其为“赵爽弦图”(如图),图由弦图变化得到,它是由八个全等的直角三角形拼接而成,记图中正方形 、正方形 、正方形 的面积分别为 、 、 .若正方形 的边长为5,则 .
三、解答题
-
19. 计算: .20. 先化简,再求值: ,其中 .21. 如图, 是 的直径, 与 相交于点 , .
 (1)、求证: 是 的切线.(2)、若 , ,求直径 的长度.22. 某市举行“文明城市”书画比赛,已知每篇参赛作品成绩记作 分 ,组委会从1000篇作品中随机抽取了部分参赛作品,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.
(1)、求证: 是 的切线.(2)、若 , ,求直径 的长度.22. 某市举行“文明城市”书画比赛,已知每篇参赛作品成绩记作 分 ,组委会从1000篇作品中随机抽取了部分参赛作品,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.书画比赛成绩频数分布表
分数段
频数
频率
38
0.38
0.29
10
0.1
合计
1

请根据以上信息,解决下列问题:
(1)、书画比赛成绩频数分布表中b的值是(2)、补全书画比赛成绩频数分布直方图.(3)、若80分以上(含80分)的书画将被评为一等奖,试估计全市获得一等奖作品的篇数.23. 某校为了举办“植树节”活动,计划购买甲、乙两种树苗,已知购买2棵甲种树苗和3棵乙种树苗共需60元,购买3棵甲种树苗和2棵乙种树苗共需65元.(1)、求每棵甲种树苗和每棵乙种树苗的价格分别为多少元?(2)、学校计划购买甲种树苗和乙种树苗共50棵,总费用不超过600元,那么最多可购买甲种树苗多少棵?24. 某县城为加快 网络信号覆盖,在高度 为90米的小山顶上架设了信号发射塔,如图所示.小茜为了知道发射塔的高度,从地面上的一点 测得发射塔顶端 点的仰角是45°,测得发射塔底部 点的仰角是30°.请你帮小茜计算出信号发射塔 的高度.(结果精确到0.1米, ) 25. 如图.在一次数学研究性学习中,小华将两个全等的直角三角形纸片 和 拼在一起,使点 与点 重合,点 与点 重合(如图),其中 ,发现四边形 是平行四边形.如图,小华继续将图中的纸片 沿 方向平移,连结 , ,当点 与点 重合时停止平移.
25. 如图.在一次数学研究性学习中,小华将两个全等的直角三角形纸片 和 拼在一起,使点 与点 重合,点 与点 重合(如图),其中 ,发现四边形 是平行四边形.如图,小华继续将图中的纸片 沿 方向平移,连结 , ,当点 与点 重合时停止平移. (1)、请问:四边形 是平行四边形吗?说明理由.(2)、如图,若 , ,当 时,请判断四边形 的形状,并说明理由.26. 如图所示,抛物线 与 轴相交于 、 两点,与 轴相交于点 ,其对称轴 与 轴相交于点 ,点 为抛物线的顶点.
(1)、请问:四边形 是平行四边形吗?说明理由.(2)、如图,若 , ,当 时,请判断四边形 的形状,并说明理由.26. 如图所示,抛物线 与 轴相交于 、 两点,与 轴相交于点 ,其对称轴 与 轴相交于点 ,点 为抛物线的顶点. (1)、求抛物线的表达式.(2)、若直线 交 轴于点 ,求证: .(3)、若点 是线段 上的一个动点,是否存在以点 、 、 为顶点的三角形与 相似.若存在,求出点 的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式.(2)、若直线 交 轴于点 ,求证: .(3)、若点 是线段 上的一个动点,是否存在以点 、 、 为顶点的三角形与 相似.若存在,求出点 的坐标;若不存在,请说明理由.