湖南省怀化市2021年初中学业水平考试数学综合检测卷(二)
试卷更新日期:2021-10-13 类型:中考模拟
一、单选题
-
1. 在数1,0,–1,–2中,最大的数是( )A、–2 B、–1 C、0 D、12.
如图,直线AB∥CD,∠B=50°,∠C=40°,则∠E等于( )
 A、70° B、80° C、90° D、100°3. 不等式3x+2≥5的解集是( )A、x≥1 B、x≥ C、x≤1 D、x≤﹣14. 下列运算正确的是( )A、 = B、2× = C、 =a D、|a|=a(a≥0)5. 函数的零点是指使函数值等于零的自变量的值,则下列函数中存在零点的是( )A、 B、 C、 D、6. 已知甲,乙两组数据的折线图如图所示,设甲,乙两组数据的方差分别为 , ,则 与 大小关系为( )
A、70° B、80° C、90° D、100°3. 不等式3x+2≥5的解集是( )A、x≥1 B、x≥ C、x≤1 D、x≤﹣14. 下列运算正确的是( )A、 = B、2× = C、 =a D、|a|=a(a≥0)5. 函数的零点是指使函数值等于零的自变量的值,则下列函数中存在零点的是( )A、 B、 C、 D、6. 已知甲,乙两组数据的折线图如图所示,设甲,乙两组数据的方差分别为 , ,则 与 大小关系为( ) A、 B、 C、 D、不能确定7. 如图,E,F分别是▱ABCD的边AD、BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到EFC′D′,ED′交BC于点G,则△GEF的周长为( )
A、 B、 C、 D、不能确定7. 如图,E,F分别是▱ABCD的边AD、BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到EFC′D′,ED′交BC于点G,则△GEF的周长为( ) A、6 B、12 C、18 D、248. 已知抛物线 ( )过 , 两点,则下列关系式一定正确的是( )A、 B、 C、 D、9. 如图,撬钉子的工具是一个杠杆,动力臂 ,阻力臂 ,如果动力F的用力方向始终保持竖直向下,当阻力不变时,则杠杆向下运动时的动力变化情况是( )
A、6 B、12 C、18 D、248. 已知抛物线 ( )过 , 两点,则下列关系式一定正确的是( )A、 B、 C、 D、9. 如图,撬钉子的工具是一个杠杆,动力臂 ,阻力臂 ,如果动力F的用力方向始终保持竖直向下,当阻力不变时,则杠杆向下运动时的动力变化情况是( )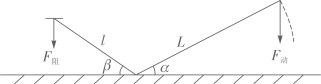 A、越来越小 B、不变 C、越来越大 D、无法确定10. 如图,在正方形 中, ,动点M自A点出发沿AB方向以每秒1cm的速度运动,同时动点N自D点出发沿折线DC-CB以每秒2cm的速度运动,到达B点时运动同时停止,设△AMN的面积为y(cm2),运动时间为x(秒),则下列图象中能大致反映y与x之间函数关系的是( )
A、越来越小 B、不变 C、越来越大 D、无法确定10. 如图,在正方形 中, ,动点M自A点出发沿AB方向以每秒1cm的速度运动,同时动点N自D点出发沿折线DC-CB以每秒2cm的速度运动,到达B点时运动同时停止,设△AMN的面积为y(cm2),运动时间为x(秒),则下列图象中能大致反映y与x之间函数关系的是( )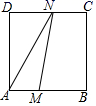 A、
A、 B、
B、 C、
C、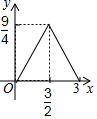 D、
D、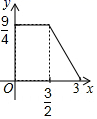
二、填空题
-
11. 某校高一年级今年计划招四个班的新生,并采取随机摇号的方法分班.小明和小红既是该校的高一新生,又是好朋友那么小明和小红分在同一班的机会是.12. 已知点 在直线 上,也在双曲线 上,则 的值为.13. 已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的侧面积为.
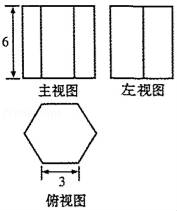 14. 如图,AB为⊙O的直径,C、D为⊙O上的点, .若∠CAB=40°,则∠CAD=.
14. 如图,AB为⊙O的直径,C、D为⊙O上的点, .若∠CAB=40°,则∠CAD=.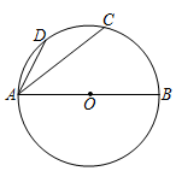 15. 设函数 与 的图象的交点坐标为 ,则 的值是.16. 如图,直线 ,直线 分别与 , 相交于点 , .小宇同学利用尺规按以下步骤作图:①以点 为圆心,任意长为半径作弧,交 于点 ,交 于点 ;②分别以 , 为圆心,大于 长为半径作弧,两弧在 内交于点 ;③作射线 交 于点 .若 , ,则线段 的长为.
15. 设函数 与 的图象的交点坐标为 ,则 的值是.16. 如图,直线 ,直线 分别与 , 相交于点 , .小宇同学利用尺规按以下步骤作图:①以点 为圆心,任意长为半径作弧,交 于点 ,交 于点 ;②分别以 , 为圆心,大于 长为半径作弧,两弧在 内交于点 ;③作射线 交 于点 .若 , ,则线段 的长为.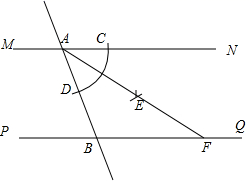
三、解答题
-
17. 计算: .18. 解不等式组 ,并求出不等式组的整数解之和.19. 甲、乙两个工程队均参与某筑路工程,先由甲队筑路60公里,再由乙队完成剩下的筑路工程,已知乙队筑路总公里数是甲队筑路总公里数的 倍,甲队比乙队多筑路20天.(1)、求乙队筑路的总公里数;(2)、若甲、乙两队平均每天筑路公里数之比为5:8,求乙队平均每天筑路多少公里.20. 如图,在平面直角坐标系 中,过点 的直线交 轴正半轴于点 .将直线 绕着点 顺时针旋转90°后,分别与 轴、 轴交于点 , .
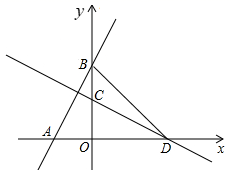 (1)、若 ,求直线 的函数表达式.(2)、连接 ,若 的面积是5,求点 的运动路径长.21. 为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分.
(1)、若 ,求直线 的函数表达式.(2)、连接 ,若 的面积是5,求点 的运动路径长.21. 为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分.分组
家庭用水量x/吨
家庭数/户
A
0≤x≤4.0
4
B
4.0<x≤6.5
13
C
6.5<x≤9.0
D
9.0<x≤11.5
E
11.5<x≤14.0
6
F
x>14.0
3
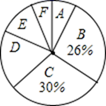
根据以上信息,解答下列问题:
(1)、本次抽样调查的家庭数为户.(2)、家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是;(3)、家庭用水量的中位数在组.(4)、若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.22. 2020年5月5日,为我国载人空间站工程研制的长征五号运较火箭在海南文昌首飞成功.运载火箭从地面 处发射、当火箭到达点 时,地面 处的雷达站测得 米,仰角为 .3秒后,火箭直线上升到达点 处,此时地面 处的雷达站测得 处的仰角为 .已知 两处相距 米,求火箭从 到 处的平均速度(结果精确到 米,参考数据: )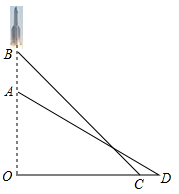 23. 在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B、C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交AB于点M.
23. 在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B、C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交AB于点M. (1)、若∠PAC=α,求∠AMQ的大小(用含α的式子表示).(2)、用等式表示线段MB与PQ之间的数量关系,并证明.24. 如图,抛物线 与直线 交于 , 两点,直线 : 交 轴于点 .点 是直线 上的动点,过点 作 轴交 于点 ,交抛物线于点 .
(1)、若∠PAC=α,求∠AMQ的大小(用含α的式子表示).(2)、用等式表示线段MB与PQ之间的数量关系,并证明.24. 如图,抛物线 与直线 交于 , 两点,直线 : 交 轴于点 .点 是直线 上的动点,过点 作 轴交 于点 ,交抛物线于点 . (1)、求抛物线 的表达式.(2)、连接 , ,当四边形 是平行四边形时,求点 的坐标.(3)、①在 轴上存在一点 ,连接 , ,当点 运动到什么位置时,以 , , , 为顶点的四边形是矩形?求出此时点 , 的坐标.
(1)、求抛物线 的表达式.(2)、连接 , ,当四边形 是平行四边形时,求点 的坐标.(3)、①在 轴上存在一点 ,连接 , ,当点 运动到什么位置时,以 , , , 为顶点的四边形是矩形?求出此时点 , 的坐标.②在①的前提下,以点 为圆心, 长为半径作圆,点 为 上一动点,求 的最大值.