湖南省常德市汉寿县2021年数学中考模拟试卷
试卷更新日期:2021-10-13 类型:中考模拟
一、单选题
-
1. -2的相反数是( )A、2 B、-2 C、 D、2. 不等式 的解是( )A、 B、 C、 D、3. 在同一副扑克牌中抽取2张“方块”,3张“梅花”,1张“红桃”.将这6张牌背面朝上,从中任意抽取1张,是“梅花”的概率为( )A、 B、 C、 D、4. 分解因式: ( )A、 B、 C、 D、5. 如图所示的正六棱柱的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 6. 古希腊几何学家海伦和我国宋代数学家秦九韶都曾提出利用三角形的三边求面积的公式,称为海伦﹣秦九韶公式:如果一个三角形的三边长分别是 , , ,记 ,那么三角形的面积为 .如图,在 中, , , 所对的边分别记为 , , ,若 , , ,则 的面积为( )
6. 古希腊几何学家海伦和我国宋代数学家秦九韶都曾提出利用三角形的三边求面积的公式,称为海伦﹣秦九韶公式:如果一个三角形的三边长分别是 , , ,记 ,那么三角形的面积为 .如图,在 中, , , 所对的边分别记为 , , ,若 , , ,则 的面积为( )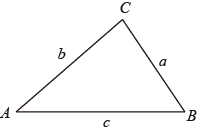 A、14 B、20 C、 D、7. 已知反比例函数 的图象分别位于第二、第四象限, 、 两点在该图象上,下列命题:①过点 作 轴, 为垂足,连接 .若 的面积为3,则 ;②若 ,则 ;③若 ,则 其中真命题个数是( )A、0 B、1 C、2 D、38. 观察等式: ; ; 已知按一定规律排列的一组数: 、 、 、 、 、 .若 ,用含 的式子表示这组数的和是( )A、 B、 C、 D、
A、14 B、20 C、 D、7. 已知反比例函数 的图象分别位于第二、第四象限, 、 两点在该图象上,下列命题:①过点 作 轴, 为垂足,连接 .若 的面积为3,则 ;②若 ,则 ;③若 ,则 其中真命题个数是( )A、0 B、1 C、2 D、38. 观察等式: ; ; 已知按一定规律排列的一组数: 、 、 、 、 、 .若 ,用含 的式子表示这组数的和是( )A、 B、 C、 D、二、填空题
-
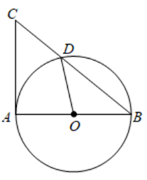
9. 计算 的结果是10. 分式方程 的解为11. 华为Mate20手机搭载了全球首款7纳米制程芯片,7纳米就是0.000000007米.数据0.000000007用科学记数法表示为 .12. 关于 的一元二次方程 有两个相等的实数根,则 的取值为13. 要使二次根式 有意义,则 的取值范围为14. 如图, 是 的直径, 是 的切线, 为切点, 与 交于点 ,连结 .若 ,则 的度数为
 15. 如图所示,在 中, , 是斜边 上的中线, 、 分别为 、 的中点,若 ,则
15. 如图所示,在 中, , 是斜边 上的中线, 、 分别为 、 的中点,若 ,则 16. 对于一个函数,自变量 取 时,函数值 也等于 ,我们称 为这个函数的不动点.如果二次函数 有两个相异的不动点 , ,则
16. 对于一个函数,自变量 取 时,函数值 也等于 ,我们称 为这个函数的不动点.如果二次函数 有两个相异的不动点 , ,则三、解答题
-
17. 计算:18. 求不等式组 的解集.19. 先化简,再求值: ,其中 .20. 每年夏季全国各地总有未成年人因溺水而丧失生命,令人痛心疾首.今年某校为确保学生安全,开展了“远离溺水•珍爱生命”的防溺水安全知识竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,共分成四组:A.80≤x<85,B.85≤x<90,C.90≤x<95,D.95≤x≤100),下面给出了部分信息:七年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82;八年级10名学生的竞赛成绩在C组中的数据是:94,90,94.七、八年级抽取的学生竞赛成绩统计表
年级
七年级
八年级
平均数
92
92
中位数
93
b
众数
c
100
方差
52
50.4

根据以上信息,解答下列问题:
(1)、直接写出上述图表中a,b,c的值;(2)、根据以上数据,你认为该校七、八年级中哪个年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);(3)、该校七、八年级共720人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀(x≥90)的学生人数是多少?21. 如图,双曲线 经过点P(2,1),且与直线y=kx﹣4(k<0)有两个不同的交点. (1)、求m的值.(2)、求k的取值范围.22. 已知如图:AB是⊙O的直径,AM和BN是⊙O的两条切线,DC与⊙O相切于点E,分别交AM、BN于D、C两点.
(1)、求m的值.(2)、求k的取值范围.22. 已知如图:AB是⊙O的直径,AM和BN是⊙O的两条切线,DC与⊙O相切于点E,分别交AM、BN于D、C两点.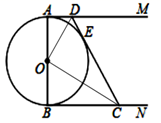 (1)、求证:(2)、求证:23. 某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,某村组织村民加工包装土特产销售给游客,以增加村民收入.已知某种士特产每袋成本10元.试销阶段每袋的销售价x(元)与该士特产的日销售量y(袋)之间的关系如表:
(1)、求证:(2)、求证:23. 某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,某村组织村民加工包装土特产销售给游客,以增加村民收入.已知某种士特产每袋成本10元.试销阶段每袋的销售价x(元)与该士特产的日销售量y(袋)之间的关系如表:x(元)
15
20
30
…
y(袋)
25
20
10
…
若日销售量y是销售价x的一次函数,试求:
(1)、日销售量y(袋)与销售价x(元)的函数关系式;(2)、假设后续销售情况与试销阶段效果相同,要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元?每日销售的最大利润是多少元?24. 某品牌太阳能热水器的实物图和横断面示意图如图所示.已知真空集热管DE与支架CB所在直线相交于点O,且 ;支架BC与水平线AD垂直. , , ,另一支架AB与水平线夹角 ,求OB的长度(结果精确到1cm;温馨提示: , , )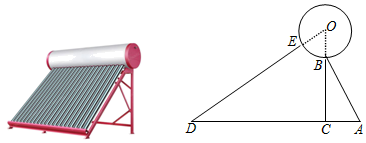 25. 如图,抛物线 过点 ,且与直线 交于 、 两点,点 的坐标为 .
25. 如图,抛物线 过点 ,且与直线 交于 、 两点,点 的坐标为 . (1)、求抛物线的解析式;(2)、点 为抛物线上位于直线 上方的一点,过点 作 轴交直线 于点 ,点 为对称轴上一动点,当线段 的长度最大时,求 的最小值;(3)、设点 为抛物线的顶点,在 轴上是否存在点 ,使 ?若存在,求点 的坐标;若不存在,请说明理由.26. 如图,正方形 的边长为2, 为 的中点, 是 延长线上的一点,连接 交 于点 , .
(1)、求抛物线的解析式;(2)、点 为抛物线上位于直线 上方的一点,过点 作 轴交直线 于点 ,点 为对称轴上一动点,当线段 的长度最大时,求 的最小值;(3)、设点 为抛物线的顶点,在 轴上是否存在点 ,使 ?若存在,求点 的坐标;若不存在,请说明理由.26. 如图,正方形 的边长为2, 为 的中点, 是 延长线上的一点,连接 交 于点 , . (1)、求 的值;(2)、如图1,连接 ,在线段 上取一点 ,使 ,连接 ,求证: ;(3)、如图2,过点 作 于点 ,在线段 上取一点 ,使 ,连接 , .将 绕点 旋转,使点 旋转后的对应点 落在边 上.请判断点 旋转后的对应点 是否落在线段 上,并说明理由.
(1)、求 的值;(2)、如图1,连接 ,在线段 上取一点 ,使 ,连接 ,求证: ;(3)、如图2,过点 作 于点 ,在线段 上取一点 ,使 ,连接 , .将 绕点 旋转,使点 旋转后的对应点 落在边 上.请判断点 旋转后的对应点 是否落在线段 上,并说明理由.