湖北省十堰市房县2021年九年级下学期初中毕业生模拟考试数学试卷
试卷更新日期:2021-10-13 类型:中考模拟
一、单选题
-
1. 下列各组数中,互为相反数的是( )A、2和-2 B、-2和 C、-2和 D、 和22. 如图,将一张含有 角的三角形纸片的两个顶点放在直尺的两条对边上,若 ,则 的度数是( )
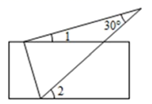 A、 B、 C、 D、3. 由四个相同的小正方体搭建了一个积木,它的三视图如图所示,则这个积木可能是( )
A、 B、 C、 D、3. 由四个相同的小正方体搭建了一个积木,它的三视图如图所示,则这个积木可能是( )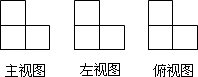 A、
A、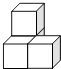 B、
B、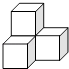 C、
C、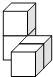 D、
D、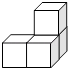 4. 下列计算正确的是( )A、a4+a5=a9 B、(2a2b3)2=4a4b6 C、﹣2a(a+3)=﹣2a2+6a D、(2a﹣b)(a-b)=2a2﹣b25. 某中学为了让学生的跳远在中考体育测试中取得满意的成绩,在锻炼一个月后,学校对九年级一班的45名学生进行测试,成绩如下表:
4. 下列计算正确的是( )A、a4+a5=a9 B、(2a2b3)2=4a4b6 C、﹣2a(a+3)=﹣2a2+6a D、(2a﹣b)(a-b)=2a2﹣b25. 某中学为了让学生的跳远在中考体育测试中取得满意的成绩,在锻炼一个月后,学校对九年级一班的45名学生进行测试,成绩如下表:跳远成绩(cm)
160
170
180
190
200
220
人数
3
9
6
9
15
3
这些运动员跳远成绩的中位数和众数分别是( )
A、190,200 B、9,9 C、15,9 D、185,2006. 在应对新冠肺炎疫情过程中,5G为山西疫情防控,复工复产,停课不停学提供了便利条件.已知5G网络峰值速率为4G网络峰值速率的10倍,在峰值速率下传输1000兆数据,5G网络比4G网络快9秒.若设4G网络的峰值速率为每秒传输x兆数据.则根据题意所列方程正确的是( ) A、 ﹣ =9 B、 ﹣ =9 C、 ﹣ =9 D、 ﹣ =97. 小致利用测角仪和皮尺测量学校旗杆的高度,如图,小致在 处测得顶端 的仰角∠ = , 到旗杆的距离 =5米,测角仪 的高度为1米,则旗杆 的高度表示为( ).
A、 ﹣ =9 B、 ﹣ =9 C、 ﹣ =9 D、 ﹣ =97. 小致利用测角仪和皮尺测量学校旗杆的高度,如图,小致在 处测得顶端 的仰角∠ = , 到旗杆的距离 =5米,测角仪 的高度为1米,则旗杆 的高度表示为( ).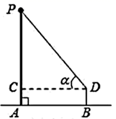 A、5 +1 B、5 +1 C、5 +1 D、 +18. 如图, 是 的直径, 是 上的三等分点,且 ,则 等于 ( )
A、5 +1 B、5 +1 C、5 +1 D、 +18. 如图, 是 的直径, 是 上的三等分点,且 ,则 等于 ( )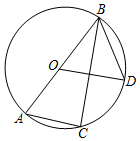 A、120° B、95° C、105° D、150°9. 将连续正整数按如图所示的位置顺序排列:根据排列规律,则2021应在( )
A、120° B、95° C、105° D、150°9. 将连续正整数按如图所示的位置顺序排列:根据排列规律,则2021应在( )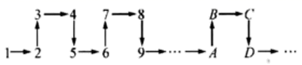 A、A处 B、B处 C、C处 D、D处10. 如图,在平行四边形ABCD中,AB⊥BD,sinA= ,将平行四边形ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线y= (k>0)同时经过B、D两点,则k的值为( )
A、A处 B、B处 C、C处 D、D处10. 如图,在平行四边形ABCD中,AB⊥BD,sinA= ,将平行四边形ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线y= (k>0)同时经过B、D两点,则k的值为( )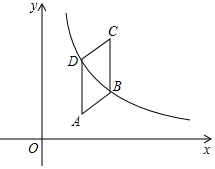 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
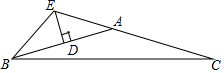
11. 如图,在△ABC中,AB=AC,AB的垂直平分线DE交CA的延长线于点E,垂足为D,∠CBE=69°.则∠C=°.
 12. 若a-2b=-2,则代数式4a2-16ab+16b2的值为.13. 数学家发明了一种魔术盒,当任意数(a,b)进入其中时,会得到一个新的数:a2+b+1,例如把(3,﹣2)放入其中就会得到32+(﹣2)+1=8,现将一数对(﹣2,3)放入其中得到数m,则m= .14. 如图,圆心角为 的扇形 内,以 为直径作半圆,连接 .若阴影部分的面积为 ,则 .
12. 若a-2b=-2,则代数式4a2-16ab+16b2的值为.13. 数学家发明了一种魔术盒,当任意数(a,b)进入其中时,会得到一个新的数:a2+b+1,例如把(3,﹣2)放入其中就会得到32+(﹣2)+1=8,现将一数对(﹣2,3)放入其中得到数m,则m= .14. 如图,圆心角为 的扇形 内,以 为直径作半圆,连接 .若阴影部分的面积为 ,则 .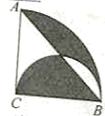 15. 如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E.若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值是.
15. 如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E.若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值是.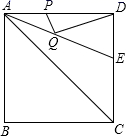
三、解答题
-
16. 计算:∣-2∣+2sin30°- -( -π)0;17. 化简:( )×18. 节能灯根据使用寿命分为优等品、正品和次品三个等级,其中使用寿命大于或等于8000小时的节能灯是优等品,使用寿命小于6000小时的节能灯是次品,其余的节能灯是正品,质检部门对某批次的一种节能灯(共200个)的使用寿命进行追踪调查,并:将结果整理成下表(假设节能灯的使用寿命均不超过9000小时).
寿命t/时
频数
频率
10
0.05
20
a
80
0.4
b
0.15
60
c
合计
200
1
(1)、根据表中的数据,求a,b,c的值;(2)、某人从这200个节能灯中随机购买1个,求这个,节能灯恰好不是次品的概率.19. 已知x1、x2是关于x的﹣元二次方程(a﹣6)x2+2ax+a=0的两个实数根.(1)、求a的取值范围;(2)、若(x1+1)(x2+1)是负整数,求实数a的整数值.20. 如图,在矩形ABCD中,P是AD上一动点,O为BD的中点,连接PO并延长,交BC于点Q.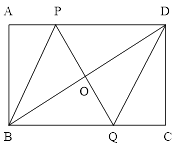 (1)、求证:四边形PBQD是平行四边形(2)、若AD=6cm,AB=4cm, 点P从点A出发,以1cm/s的速度向点D运动(不与点D重合),设点P运动时间为t s , 请用含t的代数式表示PD的长,并求出当t为何值时,四边形PBQD是菱形。并求出此时菱形的周长。21. 如图,CE是⊙O的直径,BC切⊙O于点C,连接OB,作ED∥OB交⊙O于点D,BD的延长线与CE的延长线交于点A.
(1)、求证:四边形PBQD是平行四边形(2)、若AD=6cm,AB=4cm, 点P从点A出发,以1cm/s的速度向点D运动(不与点D重合),设点P运动时间为t s , 请用含t的代数式表示PD的长,并求出当t为何值时,四边形PBQD是菱形。并求出此时菱形的周长。21. 如图,CE是⊙O的直径,BC切⊙O于点C,连接OB,作ED∥OB交⊙O于点D,BD的延长线与CE的延长线交于点A.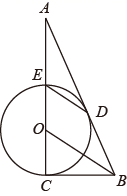 (1)、求证:AB是⊙O的切线;(2)、若⊙O的半径为1,tan∠DEO = ,求AE的长.22. 公司经销某种商品,经研究发现,这种商品在未来40天的销售单价 (元/千克)和成本价 (元/千克)关于时间 的函数关系式分别为 ( ,且 为整数); ,他们的图象如图1所示,未来40天的销售量 (千克)关于时间 的函数关系如图2的点列所示.
(1)、求证:AB是⊙O的切线;(2)、若⊙O的半径为1,tan∠DEO = ,求AE的长.22. 公司经销某种商品,经研究发现,这种商品在未来40天的销售单价 (元/千克)和成本价 (元/千克)关于时间 的函数关系式分别为 ( ,且 为整数); ,他们的图象如图1所示,未来40天的销售量 (千克)关于时间 的函数关系如图2的点列所示.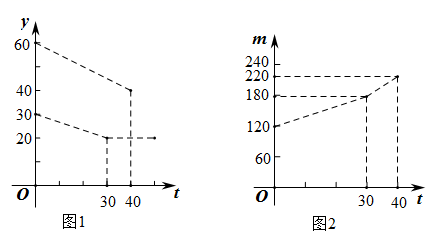 (1)、求 关于 的函数关系式;(2)、哪一天的销售利润最大,最大利润是多少?(3)、若在最后10天,公司决定每销售1千克产品就捐赠 元给“环保公益项目”,且希望扣除捐赠后每日的利润不低于3600元以维持各种开支,求 的最大值(精确到0.01元).23. △ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°.
(1)、求 关于 的函数关系式;(2)、哪一天的销售利润最大,最大利润是多少?(3)、若在最后10天,公司决定每销售1千克产品就捐赠 元给“环保公益项目”,且希望扣除捐赠后每日的利润不低于3600元以维持各种开支,求 的最大值(精确到0.01元).23. △ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°.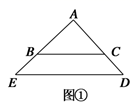
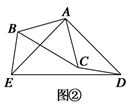
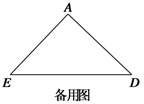 (1)、如图①,点B在线段AE上,点C在线段AD上,请直接写出线段BE与线段CD的数量关系:;(2)、如图②,将图①中的△ABC绕点A顺时针旋转,旋转角为α(0°<α<360°),请判断并证明线段BE与线段CD的数量关系;(3)、将图①中的△ABC绕点A顺时针旋转,旋转角为α(0°<α<360°),若DE=2AC,在旋转的过程中,当以A、B、C、D四点为顶点的四边形是平行四边形时,请直接写出旋转角α的度数.24. 如图,在平面直角坐标系中,直线y= x﹣4与抛物线y= +bx+c交于坐标轴上两点A、C,抛物线与x轴另一交点为点B;
(1)、如图①,点B在线段AE上,点C在线段AD上,请直接写出线段BE与线段CD的数量关系:;(2)、如图②,将图①中的△ABC绕点A顺时针旋转,旋转角为α(0°<α<360°),请判断并证明线段BE与线段CD的数量关系;(3)、将图①中的△ABC绕点A顺时针旋转,旋转角为α(0°<α<360°),若DE=2AC,在旋转的过程中,当以A、B、C、D四点为顶点的四边形是平行四边形时,请直接写出旋转角α的度数.24. 如图,在平面直角坐标系中,直线y= x﹣4与抛物线y= +bx+c交于坐标轴上两点A、C,抛物线与x轴另一交点为点B;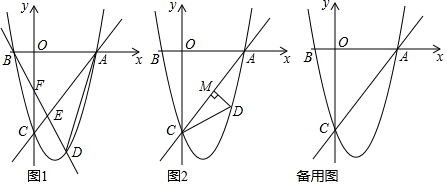 (1)、求抛物线解析式;(2)、若动点D在直线AC下方的抛物线上;
(1)、求抛物线解析式;(2)、若动点D在直线AC下方的抛物线上;①作直线BD,交线段AC于点E,交y轴于点F,连接AD;求△ADE与△CEF面积差的最大值,及此时点D的坐标;
②如图2,作DM⊥直线AC,垂足为点M,是否存在点D,使△CDM中某个角恰好是∠ACO的一半?若存在,直接写出点D的横坐标;若不存在,说明理由.