广西柳州市柳北区2021年九年级数学第三次联考试卷
试卷更新日期:2021-10-13 类型:中考模拟
一、单选题
-
1. 下列各数中,最小的数是( )A、-3 B、 C、2 D、02. 下列运算中,结果正确的是( )A、4a﹣a=3a B、a10÷a2=a5 C、a2+a3=a5 D、a3•a4=a123. 下列图形分别是桂林、湖南、甘肃、佛山电视台的台徽,其中为中心对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 4. 如图,OA⊥OB,若∠1=40°,则∠2的度数是( )
4. 如图,OA⊥OB,若∠1=40°,则∠2的度数是( ) A、20° B、40° C、50° D、60°5. 某校有19名同学参加某比赛,预赛成绩各不同,要取前10名参加决赛,小颖已经知道了自己的成绩,她想知道自己能否进入决赛,只需要再知道这19名同学成绩的( )A、最高分 B、中位数 C、极差 D、平均数6.
A、20° B、40° C、50° D、60°5. 某校有19名同学参加某比赛,预赛成绩各不同,要取前10名参加决赛,小颖已经知道了自己的成绩,她想知道自己能否进入决赛,只需要再知道这19名同学成绩的( )A、最高分 B、中位数 C、极差 D、平均数6.如图,是由一个圆柱体和一个长方体组成的几何体.其主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 7. 已知:如图, ,添加下列一个条件仍不能判定 的是( )
7. 已知:如图, ,添加下列一个条件仍不能判定 的是( ) A、 B、 C、 D、8. 20位同学在植树节这天共种了52棵树苗,其中男生每人种3棵,女生每人种2棵.设男生有x人,女生有y人,根据题意,列方程组正确的是( )A、 B、 C、 D、9. 一组数1,1,2,x,5,y…满足“从第三个数起,每个数都等于它前面的两个数之和”,那么这组数中y表示的数为( )A、8 B、9 C、13 D、1510. 如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程s之间的变化关系用图象刻画出来,大致图象是( )
A、 B、 C、 D、8. 20位同学在植树节这天共种了52棵树苗,其中男生每人种3棵,女生每人种2棵.设男生有x人,女生有y人,根据题意,列方程组正确的是( )A、 B、 C、 D、9. 一组数1,1,2,x,5,y…满足“从第三个数起,每个数都等于它前面的两个数之和”,那么这组数中y表示的数为( )A、8 B、9 C、13 D、1510. 如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程s之间的变化关系用图象刻画出来,大致图象是( )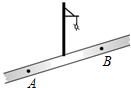 A、
A、 B、
B、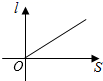 C、
C、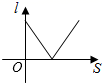 D、
D、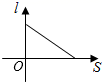 11. 如图,菱形ABCD的对角线AC,BD相交于点O,AC=8,BD=6,以AB为直径作一个半圆,则图中阴影部分的面积为( )
11. 如图,菱形ABCD的对角线AC,BD相交于点O,AC=8,BD=6,以AB为直径作一个半圆,则图中阴影部分的面积为( ) A、25π-6 B、 -6 C、 -6 D、 -612. 如图,在边长为6的正方形 内作 , 交 于点 , 交 于点 ,连接 ,将 绕点 顺时针旋转 得到 .若 ,则下列结论:① ;② ;③ ;④ .其中正确的是( )
A、25π-6 B、 -6 C、 -6 D、 -612. 如图,在边长为6的正方形 内作 , 交 于点 , 交 于点 ,连接 ,将 绕点 顺时针旋转 得到 .若 ,则下列结论:① ;② ;③ ;④ .其中正确的是( ) A、①②③④ B、①②④ C、①③④ D、③④
A、①②③④ B、①②④ C、①③④ D、③④二、填空题
-
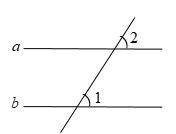
13. 使代数式 有意义的x的取值范围是 .14. 如图, ,若 ,则 .
 15. 一个袋子中有6个红球和若干个白球,这些球除颜色外,形状、大小、质地完全相同,在看不到的条件下,随机摸出一个红球的概率是 ,则袋中有个白球.16. 如图,正五边形两条对称轴所夹的 为度.
15. 一个袋子中有6个红球和若干个白球,这些球除颜色外,形状、大小、质地完全相同,在看不到的条件下,随机摸出一个红球的概率是 ,则袋中有个白球.16. 如图,正五边形两条对称轴所夹的 为度. 17. 与 相似,且 与 的相似比是 ,已知 的面积是5,则 的面积是.18. 如图, 是 的一条弦,点 是 上的一动点,且 .另一条弦 经过 、 中点 , .若 的半径为4,则 的最大值为.
17. 与 相似,且 与 的相似比是 ,已知 的面积是5,则 的面积是.18. 如图, 是 的一条弦,点 是 上的一动点,且 .另一条弦 经过 、 中点 , .若 的半径为4,则 的最大值为.
三、解答题
-
19. .20. 先化简,再求值: ,其中 .21. 在矩形 中,对角线 、 交于 点, 、 分别是 、 的中点,连接 、 .
 (1)、依题意,补全图形,并求证: ;(2)、若 ,连接 、 ,则四边形 菱形(填“是”或“不是”).22. 某校为了解学生对“ :古诗词, :国画, :闽剧, :书法”等中国传统文化项目的喜爱情况,在全校范围内随机抽取部分学生进行问卷调查(每人限选一项),并将调查结果绘制成如下不完整的统计图,根据图中的信息解答下列问题:
(1)、依题意,补全图形,并求证: ;(2)、若 ,连接 、 ,则四边形 菱形(填“是”或“不是”).22. 某校为了解学生对“ :古诗词, :国画, :闽剧, :书法”等中国传统文化项目的喜爱情况,在全校范围内随机抽取部分学生进行问卷调查(每人限选一项),并将调查结果绘制成如下不完整的统计图,根据图中的信息解答下列问题: (1)、在这次调查中,一共调查了名学生;(2)、请把折线统计图补充完整;(3)、若该校在 , , , 四项中任选两项成立课外兴趣小组,请用画树状图或列表的方法求恰好选中项目 和 的概率.23. 如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点 处的求救者后,又发现点 正上方点 处还有一名求救者.在消防车上点 处测得点 和点 的仰角分别是 和 ,点 距地面2.5米,点 距地面8.5米.为救出点 处的求救者,云梯需要继续上升的高度 为多少米?
(1)、在这次调查中,一共调查了名学生;(2)、请把折线统计图补充完整;(3)、若该校在 , , , 四项中任选两项成立课外兴趣小组,请用画树状图或列表的方法求恰好选中项目 和 的概率.23. 如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点 处的求救者后,又发现点 正上方点 处还有一名求救者.在消防车上点 处测得点 和点 的仰角分别是 和 ,点 距地面2.5米,点 距地面8.5米.为救出点 处的求救者,云梯需要继续上升的高度 为多少米? 24. 反比例函数 的图象的一支位于第一象限.
24. 反比例函数 的图象的一支位于第一象限. (1)、判断该函数图象的另一支所在的象限,并求 的取值范围;(2)、如图,若直线 与该函数图象交于 、 两点,求此反比例函数的解析式;(3)、在(2)的条件下, 的面积为8,动点 在 轴上运动,当线段 与 之差最大时,求点 坐标.
(1)、判断该函数图象的另一支所在的象限,并求 的取值范围;(2)、如图,若直线 与该函数图象交于 、 两点,求此反比例函数的解析式;(3)、在(2)的条件下, 的面积为8,动点 在 轴上运动,当线段 与 之差最大时,求点 坐标.


