广东省高州市2020-2021学年高一上学期数学期末考试试卷
试卷更新日期:2021-10-13 类型:期末考试
一、单选题
-
1. ( )A、 B、 C、 D、2. 已知 , ,则 ( )A、 B、 C、 D、3. 函数 的零点所在区间是( )A、 B、 C、 D、4. 设函数 若 ,则 ( )A、-1 B、-2 C、-3 D、-45. 若 ,则 ( )A、6 B、-6 C、 D、6. 设命题甲: , 是真命题,命题乙:函数 在 上单调递减是真命题,那么乙是甲的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件7. 函数 的图象大致为( )A、
 B、
B、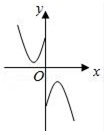 C、
C、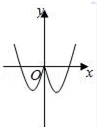 D、
D、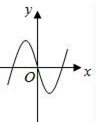 8. 已知 ,则 ( )A、 B、 C、 D、9. 已知全集 ,函数 的定义域为 ,集合 ,则下列结论正确的是( )A、 B、 C、 D、
8. 已知 ,则 ( )A、 B、 C、 D、9. 已知全集 ,函数 的定义域为 ,集合 ,则下列结论正确的是( )A、 B、 C、 D、二、多选题
-
10. 已知 ,则下列不等式一定成立的是( )A、 B、 C、 D、11. 已知函数 的图象关于直线 对称,则( )A、函数 为奇函数 B、函数 在 上单调递增 C、若 ,则 的最小值为 D、函数 的图象向右平移 个单位长度得到函数 的图象12. 已知定义在R上的偶函数f(x),满足f(x+4)=f(x)+f(2),且在区间[0,2]上是增函数,下列命题中正确的是( )A、函数f(x)的一个周期为4 B、直线x=-4是函数f(x)图象的一条对称轴 C、函数f(x)在[-6,-5)上单调递增,在[-5,-4)上单调递减 D、函数f(x)在[0,100]内有25个零点
三、填空题
-
13. 函数 的定义域为.14. 函数 ( ,且 )的图象所经过的定点在幂函数 上,则 .15. 一种药在病人血液中的量保持在2000mg以上时才有疗效,而低于1280mg时病人就有危险.现给某病人静脉注射了这种药2500mg,如果药在血液中以每小时20%的比例衰减,那么最迟必须在注射后小时前向病人的血液补充这种药.16. 已知 ,若正数a,b满足 ,则 的最小值为.
四、解答题
-
17. 解关于x的不等式 ,其中 .18. 已知角 终边与单位圆交于点(1)、求 的值;(2)、若 ,求 的值.19. 函数 是奇函数(1)、求实数a,b的值;(2)、判断函数 在R上的单调性.20. 某单位每年需向自来水公司缴纳水费约4万元,为节约用水,决定安装1个自动污水净化设备,安装这种净水设备的成本费(单位:万元)与管线、主体装置的占地面积(单位:平方米)成正比,比例系数为0.1为了保证正常用水,安装后采用净水装置净水和自来水公司供水互补的用水模式.假设在此模式下,安装后该单位每年向自来水公司缴纳水费为 ( ,k为常数),x为安装这种净水设备的占地面积(单位:平方米)记为该单位安装这种净水设备费用与安装设备后第一年向自来水公司缴水费之和.(1)、解释 的实际意义;(2)、求y的最小值.